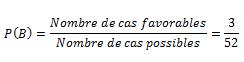Cette section a pour but de définir certains concepts, termes et procédés qui sont utilisés ou mentionnés lorsqu'il est question de probabilités.
Expérience aléatoire :
Une
expérience aléatoire est une expérience dont le résultat dépend seulement du hasard.
Celle-ci peut se dérouler en une seule ou plusieurs étapes.
Ex.:
1 étape:
- Lancer un dé
- Tirer une carte
- Lancer une pièce de monnaie
- Lancer un dé à deux reprises
- Tirer deux cartes et observer la valeur de chacune
- Lancer une pièce de monnaie plus d'une fois et observer le résultat.
L’univers des résultats possibles :
Lorsque toutes les possibilités de l'expérience ont la même chance de se réaliser, on dit que les résultats sont équiprobables.
Ex.: Lors du lancer d'un dé à six faces, l’univers des résultats possibles Ω est :
{1, 2, 3, 4,
5, 6} et se note Ω={1, 2, 3, 4,
5, 6}
Lorsque l'on tire une pièce de monnaie à deux reprise, l’univers des résultats possibles Ω est : {pile-pile, pile-face, face-pile, face-face} et se note Ω={pp, pf, fp, ff}
Évènement :
Dans une expérience qui consiste à tirer une carte d'un jeu de carte, l’événement « obtenir une figure de carreau » représente le sous-ensemble formée des résultats valet, dame et roi de carreau. Si nous nommons cet événement B, il se note comme suit: B={V◊,D◊, R◊}
Probabilité :
Une probabilité est un nombre qui quantifie les chances qu’un événement se réalise. C’est un nombre compris entre 0 et 1inclusivement. La probabilité d’obtenir un événement A se note P(A) et se calcule de la façon suivante :
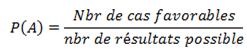
Ex.: Dans une expérience qui consiste à lancer un dé régulier à six faces, l’événement « obtenir un résultat pair » représente le sous-ensemble formée des résultats 2, 4, 6, et la probabilité de cet événement se calcule comme suit:
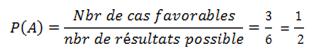
Ex.: Dans une expérience qui consiste à tirer une carte d'un jeu de cartes, l’événement
« obtenir une figure en carreau » représente le
sous-ensemble
formée des résultats
V◊,D◊, R◊
et la probabilité de cet événement se calcule comme suit: