Petits rappels concernant les ensembles
INTERSECTION DE DEUX ENSEMBLES
Le symbole  se lit
intersection. Il représente les éléments
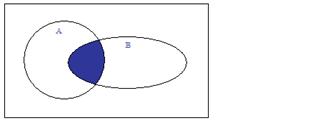
appartenant à deux ensembles. On peut le représenter grâce aux diagrammes de Venn de la façon suivante:
se lit
intersection. Il représente les éléments
appartenant à deux ensembles. On peut le représenter grâce aux diagrammes de Venn de la façon suivante:
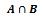
RÉUNION
DE DEUX ENSEMBLES
Le
symbole  se lit union. Il représente tous les
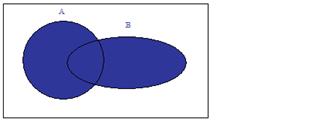
éléments des deux ensembles. On peut le représenter grâce aux diagramme de Venn de la façon suivante:
se lit union. Il représente tous les
éléments des deux ensembles. On peut le représenter grâce aux diagramme de Venn de la façon suivante:
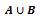
À noter: si les deux ensembles représentent deux évènements distincts, afin de pouvoir calculer la probabilité qu’un des résultats des deux ensembles se réalise, nous utilisons la formule suivante :
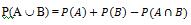
ÉVÉNEMENTS COMPATIBLES
Des
événements sont compatibles s’ils possèdent au moins 1 résultat commun,
c'est-à-dire si
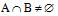
Ex. : En lançant un dé, l’évènement A Obtenir un nombre pair et l’évènement B Obtenir un nombre premier sont compatibles puisque le chiffre 2 est à la fois un nombre pair et un nombre premier. On le représente pde la façon suivante:

Deux événements A et B mutuellement exclusifs sont aussi dits incompatibles. Des événements sont incompatibles s’ils ne possèdent aucun résultat commun, donc ne peuvent pas se produire en même temps. c'est-à-dire si:
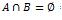

Ex.: En lançant un dé, l’évènement A={1, 5} et l’évènement B Obtenir un nombre pair sont incompatibles car 1 et 5 ne sont pas des nombres pairs.
ÉVÈNEMENTS COMPLÉMENTAIRES
Deux
événements sont complémentaires s’ils ne possèdent aucun résultat commun et si
la réunion des résultats possibles de deux événements correspond à l’univers des résultats possibles.

|
On peut donc affiirmer que la probabilité qu'un évènement se produise est de 1 moins la probabilité que son évènement complémentaire se produise.
On peut donc affirmer également que la probabilité qu’un événement ne se produise pas est donc 1 moins la probabilité qu’il se produise.
Vidéos utiles:
La résolution de problèmes concernant les probabilités