L'espérance mathématique est la moyenne pondérée des résultats d'une expérience aléatoire dans laquelle les facteurs de pondération sont les probabilités d'obtenir chacun des résultats. Elle est généralement utilisée dans des situations impliquant des gains. Il s'agit donc de la somme des probabilités de chaque résultat et des gains correspondants. Elle est censé représenter la moyenne des gains si nous exécutons un nombre élevé de fois l'expérience aléatoire dont il est question.
ESPÉRANCE MATHÉMATIQUE N'IMPLIQUANT PAS UNE MISE DE JEU
Il s’agit ici de jeux qui ne nécessite pas une mise de départ, qui ne nécessite pas de débourser de l’argent pour jouer.
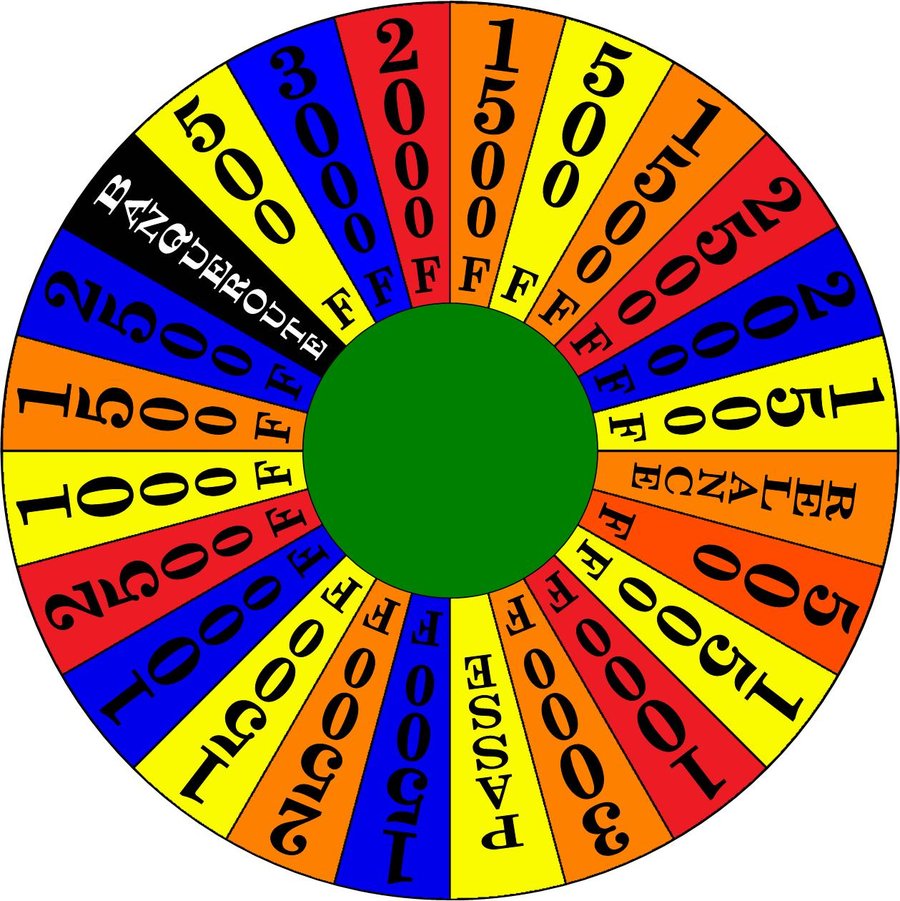
Voici donc les différents prix et la probabilité qu'ils ont de se produire:
Aucun gain: 3/24
500$: 3/24
1000$: 3/24
1500$: 7/24
2000$: 2/24
2500$: 4/24
3000$: 2/24
Si nous calculons l'espérance mathématiques, le calcul se fait comme suit:
0 x 3/24 + 500 x 3/24 + 1000 x 3/24 + 1500 x 7/24 + 2000 x 2/24 + 2500 x 4/24 + 3000 x 2/24 =
= 1458,33$
On peut donc affirmer que si nous faisons tourner la roue un grand nombre de fois, nous gagnerons, en moyenne, 1458,33$
Remarque:
- La valeur moyenne des résultats obtenus en répétant une expérience aléatoire un très grand nombre de fois tend vers l'espérance mathématique
- L'espérance mathématique d'un jeu de hasard dépend du prix à payer et des prix à gagner pour y participer.
ESPÉRANCE MATHÉMATIQUE IMPLIQUANT UNE MISE DE JEU
Espérance mathématique = probabilité x gain + probabilité x gain + ... - mise de départ
Ex.: Si nous reprenons l'exemple du haut, mais que le joueur doit miser 500$ pour tourner la roue, alors dans ce cas l'espérance mathématique ne sera plus de 1458,33$, mais bien de ce montant auquel on a enlevé 500$, c'est-à-dire 958,33$
Dans la simulation suivante, nous vous proposons d'entrer une liste de prix à gagner ainsi que la probabilité de gagner chacun de ces prix. Le fichier calculera pour vous l'espérance tout en vous donnant le détail du calcul. (Si vous n'avez pas 10 prix, laissez les 0 dans le fichier)
INTERPRÉTATION DES RÉSULTATS
Dans un eu qui consiste à effectuer une expérience
aléatoire et où il est possible de gagner ou de perdre des points, des objets
ou de l’argent, il y a trois possibilités. Le jeu est :
- Favorable à la joueuse ou au joueur si l’espérance mathématique
est positive
- Défavorable à la joueuse ou au joueur si l’espérance mathématique
est négative
- Équitable si l’espérance mathématique est nulle
Vidéos utiles:
L'espérance mathématique: