Probabilité théorique :
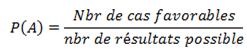
Elle
se définit comme étant un nombre qui quantifie la possibilité que l’évènement
se réalise, soit sous la forme de fraction, de pourcentage ou de nombre décimal. La probabilité peut aussi être un nombre irrationnel
comme par exemple le nombre π/4. Une probabilité doit être comprise entre 0 et 1, ou 0 et 100%.
Ex.:Si nous lançons un dé régulier à six
faces , l’événement « obtenir
un résultat
pair »
représente le sous-ensemble
formée des résultats 2, 4, 6, soit {2, 4, 6}. Les
cas
possibles sont notés comme étant
l’ensemble {1, 2, 3, 4, 5, 6}.
La
probabilité sera alors égale à 3/6, soit ½, 50% ou 0.5
Probabilité expérimentale ou fréquentielle :
La probabilité fréquentielle est une estimation faite à partir de résultats observés suite à plusieurs réalisations d'une expérience aléatoire. On doit avoir recours à une expérience aléatoire lorsqu'on ne dispose pas d'un modèle permettant de calculer une probabilité théorique. Lorsque l'expérience aléatoire est effectuée un grand nombre de fois, la probabilité fréquentielle constitue une bonne estimation de la probabilité théorique d'un événement. La probabilité expérimentale d'un événement d'une expérience aléatoire est le rapport entre le nombre de fois que cet événement se réalise et le nombre de fois que l'expérience a été réalisée.
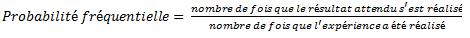
Sur un nombre relativement grand d'essais, la probabilité expérimentale ou fréquentielle d'un événement tend à se rapprocher de plus en plus de la probabilité théorique de l'événement.
Dans la simulation suivante, vous êtes invités à simuler un lancer de dé. Si vous lancez le dé une seule fois, vous aurez une probabilité fréquentielle de 1 ou 0, et non pas 1/6 comme il se devrait. Par contre, si vous effectuez la simulation un très grand nombre de fois, vous verrez que les probabilités fréquentielle se rapprochent dangereursement de la valeur théorique.
Ex.: Sur un total de 1000 lancer, le résultat face a
été obtenu 621 fois. La probabilité
fréquentielle
d'obtenir face est donc de 621/1000 =0,621
À noter:
La
probabilité de certaines expériences ne peuvent qu’être
calculées
qu’expérimentalement, contrairement au
lancer de la pièce de
monaie. Soit l’expérience
aléatoire « Lancer un
gobelet de styromousse
vide et noter sa position finale ». Il est impossible de déterminer la
probabilité théorique qu'un tel événement se
produise. (Quoique l'on puisse
en douter avec la technologie
disponible maintenant.
Voici la compilation des résultats des 50 lancers.

Probabilité subjective :
Ensuite, nous abordons la probabilité subjective. Cette probabilité repose sur le jugement ou la perception d’une personne ayant certains renseignements sur une expérience aléatoire. La probabilité est subjective car elle fait appel au jugement et correspond à une évaluation personelle basée à la fois sur des connaissances et des opinions. On évalue une probabilité subjective dans le cas où il est impossible de calculer une probabilité théorique ou d'estimer une probabilité fréquentielle.
La prévision de résultats sportifs et certaines prévisions météorologiques font appel à la probabilité subjective.
La probabilité subjective qu'un événement se réalise peut être évaluée différement d'une personne à une autre.
Ex.: Déterminer la probabilité que les Canadiens de Montréal remportent la prochaine partie contre les Bruins de Boston.
La probabilité de précipitation pour Montréal pour la journée de demain est de 40%
Probabilité géométrique :
Une probabilité géométrique est une probabilité qui implique des longueurs, des aires ou des volumes ou toute autre figure géométrique ou notion géométrique comme des angles.
Ex.: Déterminer le nombre de fois que l'on peut obtenir une région donnée sur une cible en lançant des fléchettes. Par exemple, si nous voulons atteindre une région de 15 cm² sur une cible de 100 cm², la prbabilité théorique d'obtenir la région serait de 15/100=15%. Il serait également possible de calculer la probabilité fréquentielle de cette événement en réalisant l'expérience. D'ailleurs, la simulation disponible ci-dessous simule expérience semblable.
Vous pourrez choisir l'aire de la surface et de la cible visée ainsi que le nombre de fois que vous voulez lancer une fléchette. La cible s'affichera avec tous les lancers tout en effectuant le calcul des probabilité théorique et fréquentielle de toucher la cible. Faites attention de ne pas exagérer les aires et de ne pas choisir un nombre trop élevé de lancers afin que la simulation ne dure pas trop longtemps.
À noter: Il est évident que l'on assume que les lancers se font de manière tout à fait aléatoire et qu'elles doivent obligatoirement toucher la cible. Dans la vie de tous les jours, il ne s'agit pas d'une expérience aléatoire car un joueur de fléchettes vise en lançant ce qui ne laisse plus le hasard étant le seul responsable du résultat. De plus, la fléchette ne touche pas obligatoirement la cible.
Vidéos utile
Les probabilités théoriques et fréquentielles:
http://www.youtube.com/watch?v=zhA4Ma6hUCk