PROBABILITÉ CONDITIONNELLE


        Une probabilité conditionnelle est une probabilité qu'un événement se produise sachant qu'un autre s'est déjà produit.

                    Ex.: la probabilité que j'ai obtenu un deux en lançant un dé, sachant que j'ai obtenu un                                    nombre pair.  

  • Dans l'exemple mentionné plus haut, on pourrait dire que l'événement A={obtenir un 2} et l'événement B={obtenir un nbr pair}. La probabilité d'obtenir un deux sachant que le nombre est un nombre pair se note ainsi:    P(A|B)
  • P(A|B) mesure la probabilité que A se réalise dans un univers des résultats possibles réduit à B.
  • La probabilité pour qu’un évènement A se réalise, sachant que l’événement B s’est réalisé se calcule de la façon suivante:


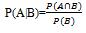
Démonstration
        Mais d’où nous vient cette formule. Nous allons la définir à l’aide des éléments qui la définissent et vous allez voir qu’on peut retrouver cette formule assez aisément.

        Premièrement, définissons certaines probabilités:

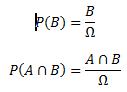
        Nous savons également que comme nous savons que l’événement B s’est produit, alors l’univers des possibles est donc B. Et le résultat de l’événement A doit se retrouver dans l’ensemble B. Autrement dit, le résultat doit appartenir à 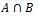 intersection. On peut donc dire que :

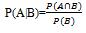
Or nous savons que:

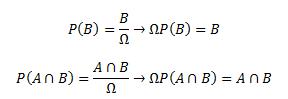
Alors:

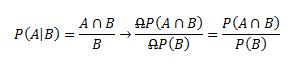
Afin de t’aider à comprendre la probabilité conditionnelle, voici un petit vidéo où on fait un exemple simple qui devrait t’aider à comprendre.

http://www.youtube.com/watch?v=8zavwr2rcS8

ÉVÉNEMENTS DÉPENDANTS

Deux événements sont dépendants si la réalisation de l’un influence la probabilité de la réalisation de l’autre.

P(A|B)≠P(A)           et           P(B|A)≠P(B)

                      Ex. : Si je te demande quelle est la probabilité de piger deux cartes dans un paquet de                                carte et de ne pas les remettre dans celui-ci. Comme tu pige une première carte,                                 il y a moins de cartes dans le paquet donc tu viens inévitablement de changer la                                 probabilité de piger toute autre carte

La probabilité que deux événements dépendants se réalisent est le produit de la probabilité que l’un d’eux se réalise par la probabilité que le second se réalisé sachant que le premier s’est réalisé (on note cette dernière probabilité P(A|B)).


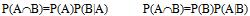
ÉVÉNEMENTS INDÉPENDANTS

Deux événements sont indépendants si la réalisation de l’un n’influence pas la probabilité de réalisation de l’autre. La probabilité que l’événement A se réalise n’est pas influencée par le fait que l’événement B se soit réalisé.

P(A|B)=P(A)       et       P(B|A)=P(B)

                    Ex. : Si je te demande quelle est la probabilité de lancer deux dés, le résultat du premier                             n’est pas influencé par le résultat du second et vice-versa. Il s’agit donc de deux                                 événements indépendants.

    • Soit A et B deux événements associés à une expérience aléatoire. A et B sont indépendants, si et seulement si,


Vidéos utiles:

Les probabilité conditionnelles:

http://www.youtube.com/watch?v=1-EL54qFjwY