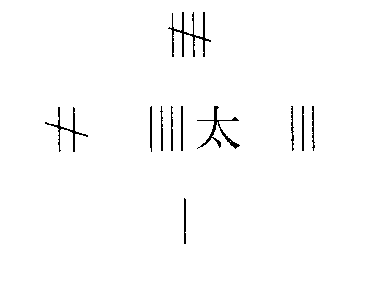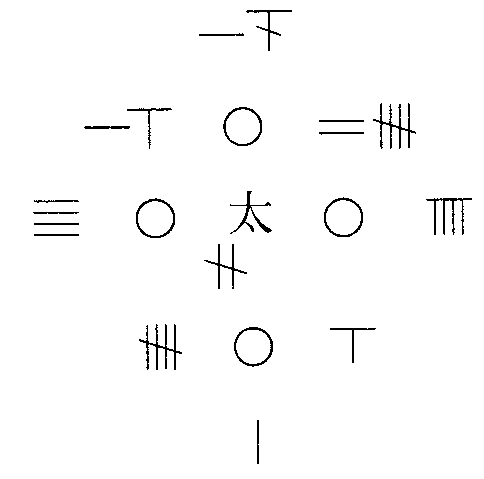Bas de la page

CHINE

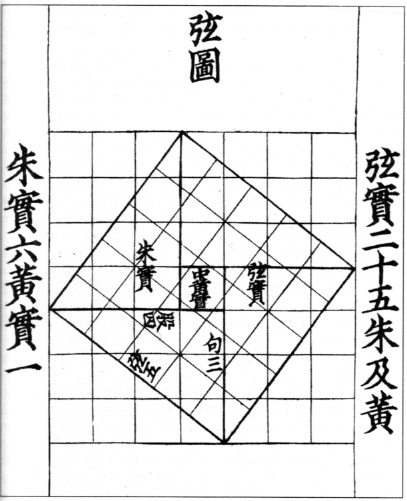
Les neuf chapitres sur l'art mathématique (Han antérieurs, (-200-0) )

Champs rectangulaires (38 problèmes) Millet et grain décortiqué (46 problèmes) Partage selon les rangs (20 problèmes) Diminution de la largeur (24 problèmes) Discussion des travaux publics (28 problèmes) Taxation équitable (28 problèmes) Excédent et déficit (20 problèmes) Comparaison des dispositions (18 problèmes) Base-hauteur (24 problèmes)

Commentaire de Liu Hui (3e siècle)

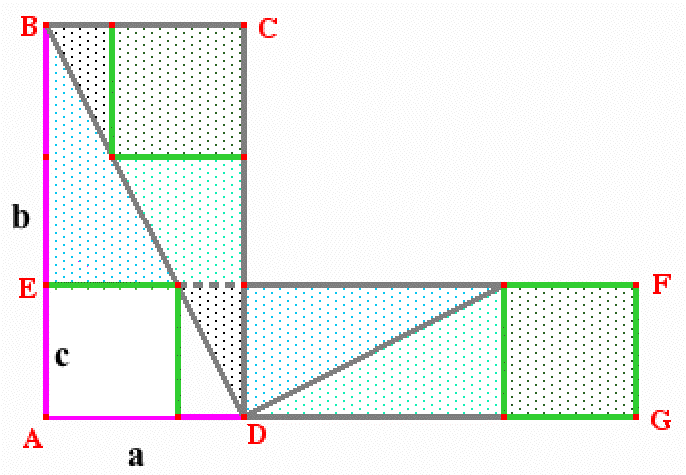
Démonstration de la résolution du problème consistant à trouver le côté du carré inscrit dans un triangle rectangle dont les cathètes sont données (a et b).

Aire de ABCD = Aire de AEFG, donc c(a+b) = ab

La trigonométrie en Chine

• Liu Hui (3e siècle)

  • Manuel mathématiques sur les îles en mer.(9 problème d'arpentage)
  • Premier problème à propos d'une île, sa distance et la hauteur du sommet.
  • Quatrième problème : la profondeur et la distance d'un point dans une vallée. (Présence implicite de la tangente)

   

• Chutan Hsita (718) Neuf planètes (Ouvrage sur les éclipses)

  • Table de sinus par sauts de 3°45'. Influence indienne sans doute, car des bouddhistes indiens sont en Chine et amène avec eux les connaissances indiennes.

 

• Yi Xing (683-727)

• 724 : étude par l'empire des ombres d'un gnomon de 8', entre le 29° et 52° de latitude, le long d'un méridien (114° est)
• Table d'ombres de 1°à 79° d'angle zénithal. s(a) =8tan(a) = 8 (sin(a)/sin(90-a) (première table des tangentes, par les tables de sinus)

Représentation des équations - Rôle du boulier

• Reflets des mesures du cercle sur la mer, Li Ye, 1248

6x² - 3x + 2 = 0

8y² - 4xy - 2x + x2

• Miroir de jade des quatre inconnues, Zhu Shijie, vers 1303

x -2y + 3z - 4w + 4 = 0

x² + 4y² + 9z² - 16u² - 4xy + 6xz + 16yu - 24zu - 2yz

Théorème de Pythagore Classique mathématique du Gnomon des Zhou, Zhao Shang, -200, +200.

Haut de la page