IFStransfos : un petit laboratoire pour les systèmes de fonctions
itérées
Ce programme permet de définir (à l'aide de la souris ou du clavier) un
ensemble de fonctions affines, puis de visualiser la figure obtenue en
itérant aléatoirement ces transformations à partir de l'origine. Pour plus
de renseignements, voir l'
article
correspondant dans Wikipedia.
Pour télécharger le programme
IFStransfos, cliquez sur l'image ci-dessus.
Mode d'emploi
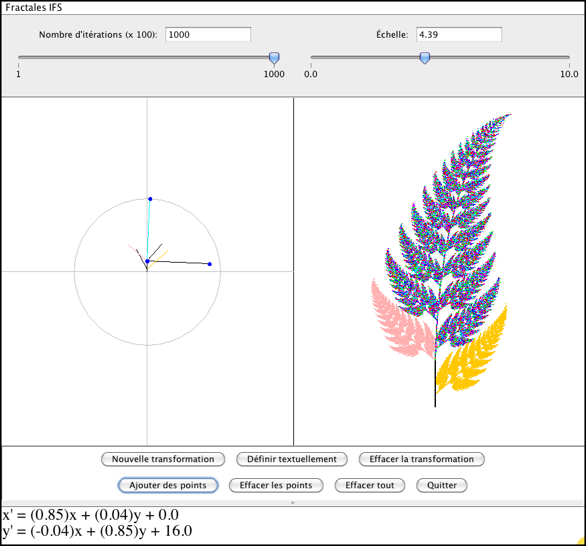
Pour ajouter une nouvelle transformation, cliquez sur le bouton
correspondant. Une nouvelle fonction affine (la fonction identité) est
créée et sélectionnée dans la portion gauche de la zone graphique. Quand
elle est sélectionnée (par un clic), une transformation est représentée
par deux segments issus d'un même point : ce point commun correspond à
l'image de l'origine par la fonction affine, tandis que les deux autres
extrémités correspondent aux images des points (1,0) et (0,1) par la même
fonction. Une fonction affine sélectionnée peut être modifiée de deux
façons :
- par la souris, en déplaçant les trois points de sa représentation
- par le clavier, en spécifiant les six paramètres de la fonction,
après avoir cliqué sur le bouton "Définir textuellement".
On peut aussi l'effacer par un clic sur le bouton correspondant.
Les points correspondant à l'itération aléatoire de ces transformations
affines sont tracés automatiquement dans la portion droite de la zone
graphique, lors de la définition des fonctions. Leur nombre est
déterminé par une glissière, et il est possible d'augmenter ce nombre
par un clic sur le bouton "Ajouter des points". Le rôle des autres
boutons est bien décrit par leurs noms.
On peut modifier certaines caractéristiques du graphique de la façon
suivante :
- l'échelle du dessin est déterminé par la glissière "Échelle"
- la position du dessin peut être modifiée en déplaçant la souris dans
la portion droite de la zone graphique tout en appuyant sur son
bouton.
Mentionnons en terminant que le menu "Fractales IFS" permet
d'enregistrer et de ramener nos systèmes de fonctions itérées. Mais ceci
ne fonctionne pas pour un applet en exécution dans un navigateur web :
il faut exécuter le programme en tant qu'application autonome sur votre
ordinateur.

