Rebonds : une illustration de la différence entre la théorie et la
pratique.
Dans plusieurs jeux, on doit faire rebondir des projectiles sur des
obstacles. Dans l'exemple stylisé ci-dessous, quand on met la balle en
mouvement, il faut calculer l'intersection de sa trajectoire avec tous les
segments en présence pour déterminer, le cas échéant, celui qu'elle frappe
en premier et sur lequel elle devra rebondir. Nous obtenons ainsi un point
de rebond à partir duquel on pourra calculer la suite de la trajectoire.
Une belle application de la
théorie mathématique!
Mais il faut se rappeler que,
en pratique, tous nos calculs se
font avec une précision limitée. Le point de rebond que nous venons de
calculer est rarement exactement sur le segment : il est souvent d'un côté
ou de l'autre de celui-ci. S'il arrive qu'il se trouve du mauvais côté, la
poursuite de la trajectoire fera à nouveau rebondir la balle sur le même
segment, mais de l'autre côté cette fois-ci. Avec le résultat que la balle
paraîtra traverser le segment.
Une solution possible, mise en oeuvre dans le programme ci-dessous, est de
négliger le segment sur lequel la balle vient de rebondir dans le calcul
du prochain rebond.
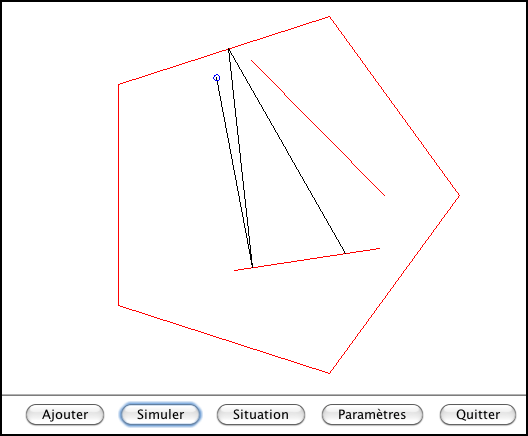
Pour télécharger le programme
Rebonds, cliquez sur l'image ci-dessus.
Mode d'emploi
La première étape est de construire les segments sur lesquels la balle
pourra rebondir (en rouge sur l'image ci-dessus).
- Un clic sur le bouton "Ajouter" ajoute un nouveau segment, qu'on
peut ensuite déplacer en saisissant ses extrémités.
- Un clic sur le bouton "Situation" permet d'ajouter un polygone
régulier (après avoir effacé tous les segments précédents).
Si désiré, on peut ensuite déplacer les segments constituant ce
polygone, ou ajouter de nouveaux segments.
La seconde étape est de spécifier les paramètres de la simulation
désirée.
- Au départ, le vecteur de mouvement est de longueur zéro et est situé
au centre de la balle. On peut saisir l'origine ou l'extrémité de ce
vecteur pour en changer la position. Lorsque le vecteur est nul, on
déplace l'extrémité du vecteur.
- Un clic sur le bouton "Paramètres" permet successivement de modifier
- le facteur d'échelle qui va déterminer la longueur totale du
trajet à partir du vecteur de mouvement
(exemple: un facteur d'échelle deux fois plus grand produit un
déplacement deux fois plus long)
- la vitesse de déplacement de la balle
(exemple: une vitesse deux fois plus grande produit un déplacement
deux fois plus rapide)
- la longueur (en nombre de segments) de la trace laissée par la
balle (en noir sur l'image ci-dessus).
On démarre la simulation par un clic sur le bouton "Simuler".

