JeuLimite : une alternance de quantificateurs illustrée par un "jeu".
Dans un jeu à deux joueurs, quand on cherche à dire que le second joueur a
une stratégie gagnante, on obtient un énoncé du type
Pour tout coup1 du premier joueur...
Il existe un coup2 du second joueur
tel que...
Pour tout coup3 du premier joueur...
Il existe un coup4 du second joueur
tel que...
...
Le second joueur gagne
On retrouve un énoncé de ce type dans la définition du concept de limite :
pour tout epsilon, il existe un delta ...
Ceci nous conduit à imaginer un jeu à deux joueurs, où le premier
donnerait des nombres epsilon positifs en guise de défi, et où le second
devrait trouver des nombres delta en guise de réponse. Voici un petit
logiciel mettant en scène cette idée.
Pour exécuter le programme
JeuLimite, cliquez sur l'image
ci-dessus.
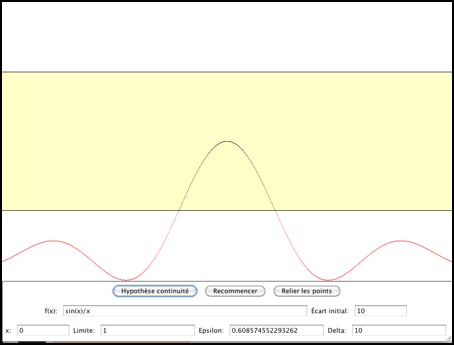
Mode d'emploi
Supposons qu'on veuille vérifier si
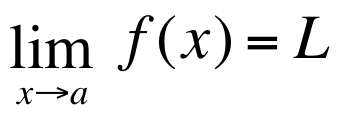
.
On doit tout d'abord entrer les informations pertinentes dans les champs :
- dans le champ "f(x)", la description de la
fonction
- dans le champ "Écart initial", le nombre E tel que le
tracé initial de la fonction se fera dans l'intervalle [a-E , a+E]
- dans le champ "x", la valeur de a
- dans le champ "Limite", la valeur de L [Note : un clic
sur le bouton "Hypothèse continuité" entrera la valeur f(a).]
Remarques importantes
- Normalement, dans Expresso, on doit utiliser le point décimal et non
la virgule. Mais, dans le présent exemple, on peut utiliser
indifféremment l'un ou l'autre, ou même un mélange des deux.
- Par défaut, le graphe sera tracé point par point. Si le résultat
vous paraît trop "espacé", vous pouvez cliquer sur le bouton "Relier
les points".
Le but du "jeu" (sans fin) est de pouvoir, pour chaque rectangle jaune
présenté par le programme, réduire ses dimensions horizontales (au moyen
de la souris) de façon à ce que tous les points du graphe de la fonction
soient contenus dans ce rectangle réduit. Si vous réussissez, le
programme vous présentera un nouveau rectangle / défi. Si vous échouez,
le programme vous le signalera, puis vous présentera un nouveau
rectangle / défi de façon à vous permettre de corriger une éventuelle
erreur de votre part. Si tout correction s'avérait impossible, c'est que
la fonction n'admet pas la limite L au point a.



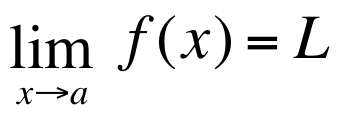 .
.