Les Arabes

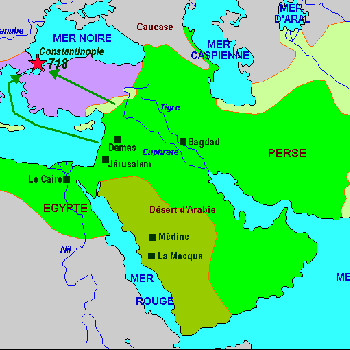Le berceau intellectuel et économique de cette nouvelle civilisation sera d'abord La Mecque, ville natale du prophète et carrefour économique de la région. Après la mort du prophète (632), les conquêtes musulmanes) se succèdent (Syrie, Jérusalem, Mésopotamie, Égypte, Iran, Chypre, Afrique du nord, Sicile, Espagne)

Les textes scientifiques (astronomie, mathématique, médecine) récoltés au cours des conquêtes sont traduits et étudiés (en particulier, arithmétique et géométrie grecque, algèbre indienne). Dès lors et jusqu'au 15e siècle, aube de la Renaissance occidentale, malgré les huit croisades de 1096 à 1270, l'hégémonie arabe s'étendra. Les mathématiciens persans, ainsi qualifiés dès lors qu'ils naquirent dans l'ancien empire Perse (actuels Turquie, Irak, Iran, Turkménistan, Ouzbekistan, Afghanistan), diffuseront en langue arabe et persane, philosophie et sciences.

Utilisant avec brio l'héritage géométrique grec, les mathématiciens arabes furent particulièrement novateurs en algèbre et en trigonométrie avec le développement de l'astronomie. Leur contribution implicite dans le renouveau des mathématiques en Europe est ainsi capitale.

Ecriture des nombres :

Les chiffres furent introduits à Bagdad à l’époque de calife Al Mançour en 773 dans un traité d’astronomie venant de l’Inde. Notre système décimal actuel, de base 10, utilise les chiffres de 0 à 9, dits arabes, mais d’origine indienne. Ces chiffres furent introduits en Europe que vers l’an 1000. Utilisés en Inde, ils furent d’abord transmis par les Arabes au monde occidental par Gerbert d’Aurelliac (938 ?-1003) qui en pris connaissance lors de son séjour en Catalogne. On devrait ainsi parler de chiffres indo-arabes.

Au moyen âge, les mathématiciens arabes utilisaient sensiblement :

Les fondements de l'algèbre : al-Khwārizmī

Dans le domaine des sciences, la civilisation musulmane s'inspire du patrimoine scientifique indou et surtout grec. Les savants musulmans vont faire avancer la plupart des sciences et leur donner leur véritable essor. Mais c’est en mathématique que les avancés sont les plus originales.

L’algèbre, en particulier, est née à Bagdad au 9^e siècle grâce à al-Khwārizmī , qui en donne les bases. Le mot algèbre apparaît dans le titre de son ouvrage "kitab al-mokhtasar fi hisab al-jabr wa al-moqabala" qu’on pourrait traduire par la "traite du calcul d’algèbre et de l’opposition". C’est l’un des livres les plus marquants de l’histoire des mathématiques. Le génie d’al-Khwārizmī est sans doute d’avoir introduit la notion d’inconnue : la chose, et de procéder à sa manipulation mathématique exactement comme un nombre connu au sein d’une équation.Ce sont également les savants musulmans qui vont faire connaître les dix chiffres du système de calcul décimal.

Dans un premier ouvrage, il expose le système décimal et les règles du calcul indien. Avec le « Kitâb al-jabr wa al-muqâbala » (Le livre du rajout et de l'équilibre), rédigé entre 813 et 833 et dédié au calife al Mamum, al-Khwārizmī pose les bases des méthodes algébriques de résolution des équations ainsi qu’une synthèse des règles héritées des grecs et des textes néo-persans. En grande partie, l’ouvrage traite de problèmes de la vie courante (partages d’héritage, droits de succession, échanges commerciaux, arpentages des terres…)

Al-Khwārizmī utilise le support géométrique pour étudier les équations algébriques en termes d’aires, comme le fit Euclid auparavant. C’est dans le même esprit qu’on prouve ainsi aisément les identités remarquables usuelles étudiées au 2e cycle du secondaire.

a² – b² = (a + b) x (a – b)

a² + b² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

Représentation moderne des liens “algèbre et géométrie” développés par al-Khwārizmī :

Autres

Shuja Abu Kamil (850 ; 930) prolonge les travaux d’al-Khwārizmī sur les équations quadratiques dans « al Kitab al kamil fi l-jabr wa l-muqabala » (Livre complet en algèbre). Son second livre « Kita bat-tara’if l-hisab (Livre des choses rares en calcul) est entièrement consacré aux systèmes d’équations. Abu Kamil possède un degré d’abstraction supérieur à son prédécesseur.

Al-Bîrunî (973-1048) a écrit un traité sur la « règle de trois » qui est en fait un traité sur le calcul des proportions. Sa plus grande contribution aux mathématiques est en trigonométrie ou il a établi des tables très précises qu’il a appliquées au cadran solaire et l’astronomie.

Al-Samawal (1130-1180) est connu pour ses travaux en algèbre des polynômes et pour son traité al-Bahir fi'l-jabr (livre flamboyant de l'algèbre) dans lequel il développe des techniques opératoires sur les polynômes, extrait des racines carrés, et présente une des premières formes de raisonnement par récurrence. Il établit également la formule de somme des carrés des premiers entiers:

Les traductions

Bagdad, ville créée par les califes abbassides pour servir de capitale de l'Empire, devient très vite un centre culturel avec notamment la création d'une Maison de la Sagesse sous le règne du calife Al-Mamun (début du IXe siècle). Un grand programme de traduction y est entrepris, d'abord de persan en arabe puis de sanscrit ou de grec en arabe.

Les Arabes établissent des contacts avec les Romains byzantins de Constantinople et les califes arabes achètent les manuscrits grecs notamment les Éléments d'Euclide (traduits par Al-Hajjaj) et la Grande composition mathématique de Ptolémée connue sous le nom Almageste qui donne lieu à plusieurs traductions dont celle d'Al-Hajjaj et celle de Thabit ibn Qurra. Deviennent également accessibles et traduits en arabe des ouvrages tels que les Coniques d'Apollonius, De la sphère et du cylindre d'Archimède, l’Arithmetica de Diophante (traduit par Qusta ibn Luqa), le Traité sur les miroirs de Dioclès, les Travaux sur la mécanique de Pappus d'Alexandrie ainsi que les traités de Héron d'Alexandrie. Les mathématiciens arabes traduisent aussi des textes sanskrits d'astronomie et de mathématiques indiennes comme le Surya Siddhanta et le Brahma Sphuta Siddhanta (traduits par Muhammad al-Fazari), le Khandakhayaka de Brahmagupta7 et l'Aryabhatiya d'Aryabhata.

Sources:

http://serge.mehl.free.fr/base/islam.html

http://estupret.com/tag/islam

https://upload.wikimedia.org/wikipedia/commons/d/df/Compa.jpg

http://www.maths-et-tiques.fr/index.php/histoire-des-maths/nombres/histoire-de-l-algebre

http://www.muslimheritage.com/sites/default/files/contribution_of_al-khwarizmi_06.jpg

https://fr.wikipedia.org/wiki/Math%C3%A9matiques_arabes

http://ecx.images-amazon.com/images/I/61myKT%2By9lL.jpg

https://fr.wikipedia.org/wiki/Ibn_Yahy%C4%81_al-Maghrib%C4%AB_al-Samaw'al