La Grèce

À la différence des mathématiques égyptiennes et mésopotamiennes connues par des papyrus ou des tablettes d'argiles antiques remarquablement bien conservées, les mathématiques grecques ne sont pas parvenues jusqu'à nous grâce à des traces archéologiques. On les connait grâce aux copies, traductions et commentaires de leurs successeurs.

Les deux domaines de la mathématique grecque sont généralement l’arithmétique et la géométrie. Si l’arithmétique a pour origine le travail des commerçants, des comptables et des navigateurs, la géométrie a la sienne dans le travail des artistes, sculpteurs, peintres, céramistes, architectes, etc.

Thalès et Pythagore fondent la science mathématique au VIe siècle av. J.-C. chez les Grecs. Pendant près d’un millénaire, ces derniers accumuleront tout un savoir arithmétique et géométrique d’où il ne faut pas oublier la logique du philosophe Aristote. Ce n’est que vers 300 av. J.-C. qu’Euclide viendra mettre les pendules à l’heure en regroupant dans ses écrits (Éléments de la mathématique de son temps), toutes les mathématiques connues et démontrées. Cet encyclopédie ordonne toutes connaissances, mais surtout elle les enchaîne logiquement, en distinguant définitions, postulats et axiomes.

Dans nos écoles, nous entendons surtout parler de deux grands mathématiciens grecs : Thalès et Pythagore. Cependant, il en existe plusieurs autres. En voici quelques-uns. Oenopide de Chios a été celui qui a réussi tracer une perpendiculaire à une droite à l’aide d’un compas.Aussi, Hippocrate a contribué à la résolution de la quadrature du cercle (construction d’un carré dont l’aire est la même qu’un cercle donné). Il a aussi posé un problème de la duplication du cube et il ne sera finalement résolu qu’au XIXe siècle! Finalement, Eudoxe de Cnibe est celui qui a résolu le problème de la section d’or qui consiste à découper un segment de droite en section dite harmonieuse.

Ecriture des nombres :

Les Grecs utilisaient un système de numération décimal additionnel codé au moyen de leur alphabet (lettres minuscules accentuées). Pour leurs comptes, ils utilisaient des abaques (du grec abax = tablette) : tablettes à rainures où glissaient des jetons, à l'instar des bouliers chinois (qu'on estime apparus au moins 5 siècles avant J.-C.).

Certains nombres avaient droit à des caractères spéciaux comme 900 (sampi). Pour distinguer un nombre d'un mot, on le surlignait. Comme on le voit ci-dessus pour le nombre 1000, la présence d'une sorte de virgule désignait une multiplication par 1000; autre exemple : ,ß = 2000. Pour exprimer une fraction unitaire, on ajoutait un "prime" à droite du nombre; par exemple, ß' = 1/2. Dans ce système additionnel :

12 s'écrit iß : 10 (i) suivi de 2 (ß), signifiant 10 + 2

Les fondements de la géométrie et de l'arithmétique :

Le terme géométrie provient du grec gê (la Terre) et metron (mesure). Dans ce contexte géométrique, l'objectif originel des anciens fut de rechercher des solutions à leurs problèmes d'arpentage et de construction (au sens architectural) mais aussi de comprendre les lois régissant notre monde (astronomie, du grec nomos : loi). Pour ce faire, ils développèrent l'arithmétique, du grec arithmêtikê, mot à mot : qui est en rapport avec le nombre : arithmos, et le calcul fractionnaire, tout particulièrement l'étude des proportions.

Chez les grecs, les nombres sont intimement liés à des concepts géométriques, de ce fait, ils n’apporteront pas de techniques nouvelles de calculs. Ils s’attacheront à passer par des constructions à la règle et au compas pour représenter les solutions qui sont nécessairement des rationnels positifs.

La synthèse la plus importante des mathématiques grecques vient des Éléments d’Euclide. Les objets géométriques doivent être définis : il ne s'agit plus d'objets imparfaits mais de l'idée parfaite des objets. Dans ses Éléments, Euclide se lance dans la première formalisation de la pensée mathématique. Cette œuvre monumentale, en treize livres, aura marqué toutes les générations de mathématiciens jusqu’à nos jours. Tout au long de son œuvre, Euclide utilise la déduction comme forme de raisonnement. Il définit les objets géométriques (droites, cercles, angles), il définit l'espace par une série d'axiomes, il démontre par implication les propriétés qui en découlent et fait le lien formel entre nombre et longueur. Cet ouvrage restera dans le cursus mathématique universitaire européen jusqu'au XIX^e siècle.

Extrait du Livre II Proposition 11 des Eléments d’Euclide.

Dans le langage d’aujourd’hui : Soit [AB] un segment donné, il s’agit de déterminer le point H de [AB] tel que le carré construit sur [AH] ait la même aire que le rectangle de côtés [HB] et [AB]. Ce qui revient à résoudre l’équation :
x² = AB(AB - x), où x = AH.

L’amorce du symbolisme en algèbre voit le jour dans « Les arithmétiques » avec Diophante d’Alexandrie (IIIe siècle) qui deviendra une référence pour la civilisation arabe, puis pour les savants de la Renaissance. Dans son livre, le mathématicien grec fait référence à des solutions fractionnaires positives. De plus, on le reconnaît pour être l’un des premiers à établir une règle des symboles dans l’écriture mathématique. Il a inventé notamment les symboles représentant les nombres invariables et l’inconnu dans une équation.

L'organisation de l'enseignement

En Grèce, l’éducation des jeunes enfants relève des femmes et des pédagogues, généralement des esclaves, puis des maîtres, vers l’âge adulte et les valeurs de la Cité antique comme le théâtre, la guerre, le sport, la politique. Éducation idéale en apparence, elle alliait le développement physique des enfants à celle des arts (musique), des valeurs morales antiques de force et de vertu (militaire), et de l’intellect (poésie). Elle procurait le développement harmonieux des corps grâce au sport vers un idéal de beauté de l’adulte.

Le maître d’écriture, pour les enfants qui ne savent pas encore écrire, trace d’abord les lettres avec son stylet et leur remet ensuite la page où ils devront suivre docilement l’esquisse des lettres. Celui qui s’en écarte est frappé d’une sanction.

À Athènes, Solon exigeait que la Cité apprenne à ses enfants la lecture, la natation et un État. Les enfants vont chez le maître instituteur (disdaskalos) grammatiste et ensuite grammatikos (de gramma, lettre) sous la conduite du pédagogue (esclave) pendant sept ans lequel leur apprenait la lecture (sur papyrus), l’écriture (sur des tablettes de cire ou des ostraca, de tessons de poterie ou des papyrus avec de l’encre) et le calcul puis les mathématiques, puis plus tard la poésie (Homère, base de l’éducation, puis Hésiode, Solon) et les lettres.

L'enseignement des maths

Il est probable que l'école grecque des mathématiques ait été influencée par les apports mésopotamiens et égyptiens. Ainsi Thalès aurait voyagé en Égypte, et il aurait pu rapporter en Grèce des connaissances en géométrie. Il travailla sur les triangles isocèles et les triangles inscrits dans un cercle.

Selon l'école pythagoricienne, « tout est nombre ». La recherche d'objets parfaits conduit les Grecs à n'accepter d'abord comme nombres que les nombres rationnels matérialisés par la notion de longueurs commensurables : deux longueurs sont commensurables s'il existe une unité dans laquelle ces deux longueurs sont entières. L'échec de cette sélection matérialisée par l'irrationalité de la racine carrée de deux les conduit à n'accepter que les nombres constructibles à la règle et au compas. Ils se heurtent alors aux trois problèmes qui vont traverser l'histoire : la quadrature du cercle, la trisection de l'angle et la duplication du cube. En arithmétique, ils mettent en place la notion de nombre pair, impair, parfait et figuré.

Thalès de Milet

Selon la légende, c’est le pharaon Amasis qui aurait lancé le défi à Thalès de trouver la hauteur de la grande pyramide de Khéops située en Égypte. C’est à partir d’un raisonnement proportionnel que le mathématicien et philosophe grec Thalès de Milet a réussi à calculer la hauteur d’une pyramide. Sa méthode était basée sur l’utilisation d’un rapport de similitude entre des triangles semblables. Il aurait ainsi mesuré la longueur au sol créée par l’ombre de la pyramide et celle de l’ombre d’un bâton à un moment précis de la journée.

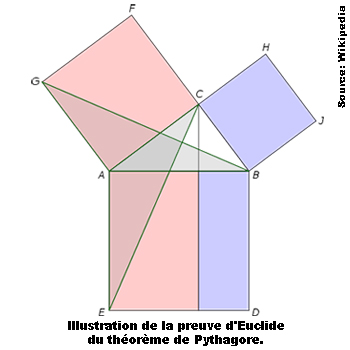Le théorème de Pythagore

Pythagore de Samos est un brillant mathématicien, philosophe et astronome de la civilisation grecque antique. Il est le fondateur de l’école pythagoricienne, institution dans laquelle les élèves apprennent la philosophie, les mathématiques et les sciences naturelles, tout en pratiquant des rituels secrets.

En géométrie, on attribue à Pythagore l’application de l’énoncé suivant :

Dans un triangle rectangle, le carré du côté opposé à l’angle droit (hypoténuse) est égal à la somme des carrés des deux autres côtés (a²+b²=c²).

Le théorème de Pythagore est également à l’origine de l’introduction les nombres irrationnels en mathématiques, c’est-à-dire les nombres réels qui ne sont pas rationnels.

Aires et volumes

Archimède de Syracuse est un géomètre et un ingénieur de la Grèce antique. Il est l’inventeur de la poulie, de la vis sans fin et de la roue dentée. En outre, il a créé différents engins de guerre, comme la catapulte, utilisés par les Grecs dans les batailles contre les Romains.

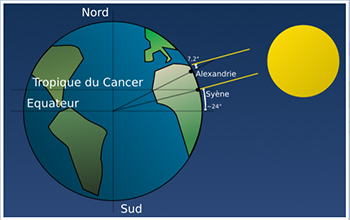Ératosthène

Plusieurs considèrent Ératosthène comme le premier géographe de l’histoire. Il s’est également illustré dans d’autres domaines tels l’astronomie, la poésie et les mathématiques.

Mathématicien, il établit le crible d'Ératosthène, méthode qui permet de déterminer par exclusion tous les nombres premiers. Il travailla sur le problème de la duplication du cube, et imagina le mésolabe, instrument propre à connaître les moyennes proportionnelles.

De nos jours, on le connaît pour avoir calculé de façon géométrique la circonférence de la Terre (ou méridien terrestre). Ses résultats reposent sur l’observation de deux villes situées sur le même méridien.

Il mesura l’ombre d’un obélisque dont il connaissait déjà la hauteur, et en déduisant l’angle que font les rayons solaires avec la verticale, il trouva 7.2o. Il utilisa cette mesure pour trouver la valeur du méridien terrestre (41 500 km), ce qui représente une marge d’erreur d’environ 3% par rapporta sa longue réelle (40 074 km).

Sources:

http://serge.mehl.free.fr/base/Grece.html

http://mathshistoire.blogspot.ca/2008/02/les-mathmatiques-chez-les-grecs.html

http://fr.wikipedia.org/wiki/Histoire_des_math%C3%A9matiques

http://fr.wikipedia.org/wiki/%C3%89ratosth%C3%A8ne

http://www.lignedutemps.qc.ca