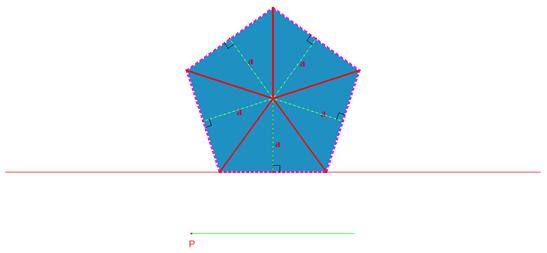
On observe ici un pentagone régulier. Le pentagone a été partionné en
cinq triangles isométriques en reliant le centre du pentagone à chacun de ses
sommets.
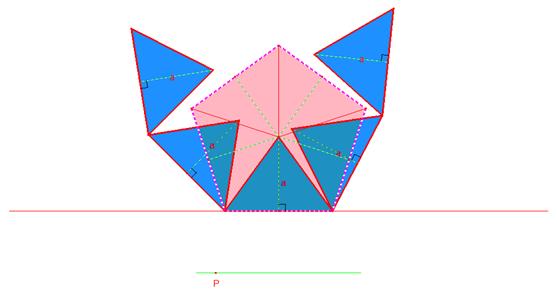
En déplaçant le point point P sur le segment
sous la construction, on observe que les triangles se déplacent de manière à ce
que leur base, c'est-à-dire le côté de chaque triangle qui, à l'origine, est
l'un des côtés du pentagone, viennent s'appuyer sur la droite horizontale. Il
est à noter que, malgré le déplacement des triangles, l'aire qu'ils
représentent est toujours la même que celle représentée par le pentagone du
départ qui est maintenant représenté par le pentagone rose.

En déplaçant le point P encore un peu, on
constate que les triangles se rapprochent de plus en plus de la droite
horizontale. Il est à noter que l'aire représentée par les triangles bleus est
toujours la même que celle représentée par le pentagone de départ qui est
maintenant représenté en rose, et ce, malgré le déplacement des triangles.
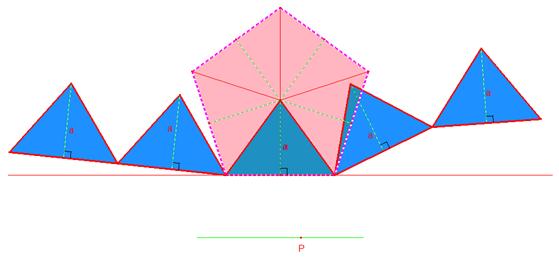
Le
point P étant presque rendu à l'extrémité du segment, les triangles sont
pratiquement appuyés sur la droite horizontale. Il est à noter que l'aire
représentée par les triangles bleus est toujours la même que celle représentée
par le pentagone de départ qui est maintenant représenté en rose, et ce, malgré
le déplacement des triangles.
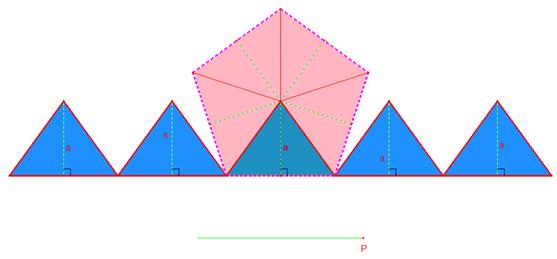
Maintenant que le point P est rendu à
l'extémité du segment, les triangles bleus sont tous appuyés sur la droite
horizontale. Sachant que l'aire représentée par les triangles bleus est
toujours la même que celle représentée par le pentagone de départ qui est
maintenant rose, nous pouvons conclure que, si nous calculons l'aire des cinq
triangles bleus, nous aurons, par le fait même, calculer l'aire du pentagone de
départ maintenant rose.
C'est d'ailleurs pour cette raison que nous avons établi qu'il est possible de
calculer l'aire du pentagone de départ en utilisant la formule qui se retrouve
au bas de ce paragraphe. En effet, pour calculer l'aire des triangles bleus, il
suffit de calculer l'aire d'un triangle et de multiplier cette aire par le
nombre de triangles, c'est-à-dire cinq dans notre cas. Pour ce faire, il suffit
de multiplier la mesure de la base d'un triangle, qui est en fait la mesure
d'un des côtés du pentagone de départ, par sa hauteur, qui correspond à
l'apothème du pentagone de départ, pour diviser le produit obtenu par deux.
Ensuite, il ne reste plus à multiplier le quotient par le nombre de triangles,
ce qui revient à multiplier par le nombre de côté du polygone de départ, qui,
dans notre cas, est un pentagone.
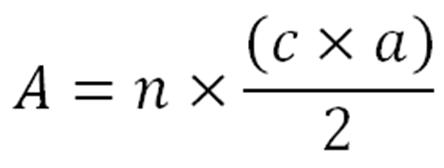
Retour à la page concernant la méthode des triangles !
