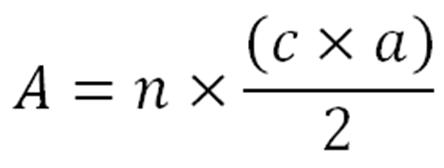
Explications de la
formule :
Il est possible de décomposer un polygone régulier en triangles.
De ce fait, un polygone
régulier a autant de triangles isométriques qu’il a de côtés. C'est
pourquoi, pour
calculer l’aire d’un polygone régulier, il est possible de commencer
par calculer l’aire d’un des triangles qui composent le polygone en
utilisant la formule 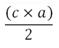 où c représente la longueur d’un côté et a
représente l’apothème du polygone régulier, c'est-à-dire la hauteur d’un triangle. Par
la suite, il ne reste plus qu'à multiplier l’aire du triangle par le nombre de
triangles qui composent le polygone régulier, soit par le nombre de côtés du
polygone.
où c représente la longueur d’un côté et a
représente l’apothème du polygone régulier, c'est-à-dire la hauteur d’un triangle. Par
la suite, il ne reste plus qu'à multiplier l’aire du triangle par le nombre de
triangles qui composent le polygone régulier, soit par le nombre de côtés du
polygone.
Par exemple, dans le
fichier suivant, nous te montrons un pentagone régulier qui peut se décomposer
en 5 triangles, c'est-à-dire autant de triangles que de côtés.
Formule modifiée pour calculer l’aire d’un
polygone régulier :
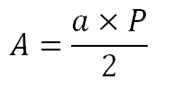
Explications de la
formule :
Cette formule découle directement de la première. En effet,
cette formule est une version simplifiée de la première, car (n x c), qui correspond au
nombre de côtés multiplié par la longueur d’un côté du polygone, nous donne le périmètre du
polygone qui est représenté par la lettre P dans la seconde formule.
À la lumière de tout ceci, il est possible de conclure que les deux formules
sont équivalentes et représentent la même chose.
Pour manipuler la construction, téléchargez le plug-in Cabri II Plus.
Il est à noter que la figure Cabri ne peut malheureusement être vue que si vous utilisez le navigateur Internet Explorer. Si ce n'est pas le cas, il vous est possible de visualier la construction ainsi que son évolution en vous rendant sur la page
Complément de la méthode des triangles .
