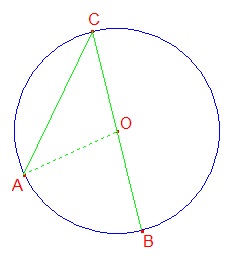
Théorème 2 - Cas 1

Ainsi, après avoir trouvé que m<AOC + m<AOB = 180°, nous obtenons les affirmations suivantes :

Affirmations	Justifications
Le triangle AOC est un triangle isocèle	Les côtés AO et CO sont des rayons du cercle. Ainsi, ils sont de même mesure.
L'angle CAO est congru à l'angle ACO	Dans un triangle isocèle, les angles opposés aux côtés congrus sont congrus.
m<ACO+m<CAO+m<AOC=180°	Car la sommes des mesures des angles intérieurs d'un triangle est de 180°
2·m<ACO+m<AOC=180°	En substituant la mesure de l'angle CAO par la mesure de l'angle ACO.
m<AOC+m<AOB=180°	Les deux angles forment un angle plat.
m<AOC = 180° - m<AOB	Par manipuations algébriques
2·m<ACO + 180° - m<AOB = 180°	En substituant la valeur de l'angle AOC par la valeur trouvée dans la quatrième étape
2·m<ACO = m<AOB	Par manipulations algébriques
m<ACO = ½·m<AOB	Par manipulations algébriques
La mesure de l'angle inscrit ACO est la moitié de la mesure de l'arc AB.	La mesure d'un angle au centre est la même que celle de l'arc qu'il intercepe