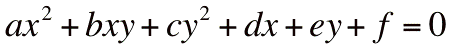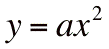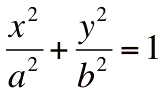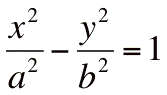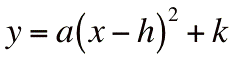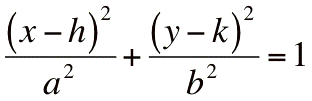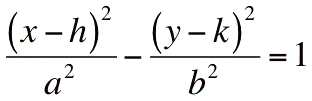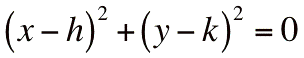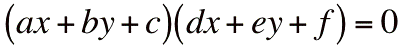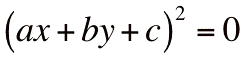|
Les courbes algébriques
Dans un contexte scolaire, on introduit souvent les coniques
via leurs équations.
Dans un premier temps, on utilise des formes simplifiées des
équations, qui supposent que les courbes sont "bien placées"
par rapport au système d'axes. Ainsi, on pourra décrire
- les paraboles via l'équation
- les ellipses via l'équation
- les hyperboles via l'équation
Par la suite, si on permet d'appliquer des translations
à nos courbes, on obtiendra les équations sous une forme un
peu plus générale
- l'équation de la parabole devient
- l'équation de l'ellipse devient
- l'équation de l'hyperbole devient
Enfin, si on permet d'appliquer aussi des rotations à nos
courbes, on obtient l'équation
générale suivante
qui couvre aussi le cas des coniques dégénérées
- un point
- deux droites
- une droite
Une dernière remarque: dans l'équation générale, on
peut supposer que tous les coefficients sont (en valeur
absolue) plus petits ou égaux à 1. (Pourquoi ?) Ceci
nous permet d'obtenir, à l'aide du logiciel GeoGebra,
une représentation dynamique de la courbe associée à
l'équation (sous sa forme générale). Notez les 6 glissières
permettant de varier gestuellement les coefficients entre -1
et +1.
Appendice
technologique
Les formules ont été créées avec l'éditeur d'équations de Microsoft
Word. À l'aide d'un clic-droit (ou d'un
contrôle-clic sur les Macintosh
ne disposant pas d'une souris à deux boutons), on les a
ensuite enregistrées en tant qu'images (au format GIF), pour
enfin les insérer dans la page web.
La figure a été créée avec GeoGebra. |