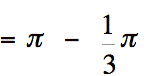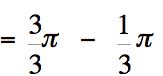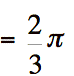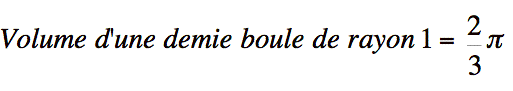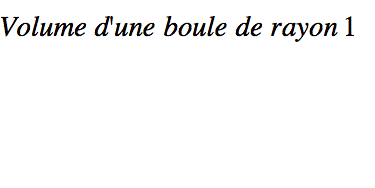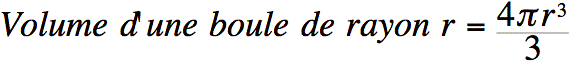Voici une boule rayon 1 unité.
Nous ne
connaissons pas son volume. Notons-le 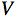 .
.
Effectuons une dilatation de facteur 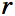 sur ses
dimensions.
sur ses
dimensions.
Nous
obtenons une boule de rayon 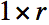 unités,
donc de rayon
unités,
donc de rayon 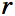 unités.
unités.
Le volume de
la boule change d'un facteur 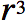 , car nous sommes
en trois dimensions.
, car nous sommes
en trois dimensions.
Nous
obtenons une boule de volume 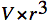 unités cubes.
unités cubes.
Remarquons que le volume de la boule de rayon 1 que nous avons noté 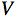 est une constante.
Par conséquent, si nous connaissions cette constante,
nous pourrions généraliser en raisonnant par dilatation de facteur
est une constante.
Par conséquent, si nous connaissions cette constante,
nous pourrions généraliser en raisonnant par dilatation de facteur 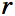 pour
connaître le volume de n'importe quelle boule de rayon
pour
connaître le volume de n'importe quelle boule de rayon 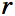 . Partons
donc, plus particulièrement à la découverte du volume d'une boule de
rayon 1 qui est notre constante
. Partons
donc, plus particulièrement à la découverte du volume d'une boule de
rayon 1 qui est notre constante 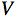 .
.
Dans le but de simplifier notre tâche, partionnons cette boule en deux demies boules de même volume. Voici un film illustrant cette subdivision:
Lire
Nous obtenons deux demies boules de rayon 1.
Déterminons le volume d'une seule de ces deux demies boules. Le volume d'une boule entière de rayon 1 nous sera donné en multipliant par 2 le volume de la demie boule trouvé. Nous ne savons pas plus trouver le volume d'une demie boule, mais nous pouvons toutefois y parvenir en se ramenant à des solides que nous connaissons. Un des solides dont nous savons déterminer le volume qui pourra nous être utile est le cylindre.
Pour ce faire, nous pouvons partionner notre demie boule de rayon 1
en 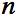 cylindres
différents. Voici un exemple avec
cylindres
différents. Voici un exemple avec 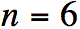 , donc
avec 6 cylindres.
, donc
avec 6 cylindres.
Bien sûr, plus 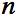 est
grand, plus la somme des volumes des cylindres ainsi
construits s'approchera du volume de la demie boule. Plus
particulièrement, pour un
est
grand, plus la somme des volumes des cylindres ainsi
construits s'approchera du volume de la demie boule. Plus
particulièrement, pour un 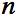 infiniment
grand, nous aurons que la somme des volumes des cylindres
sera égale au volume de la demie boule puisque les cylindres
occuperont tout l'espace disponible à l'intérieur de la demie boule. Le
film qui suit illustre la situation:
infiniment
grand, nous aurons que la somme des volumes des cylindres
sera égale au volume de la demie boule puisque les cylindres
occuperont tout l'espace disponible à l'intérieur de la demie boule. Le
film qui suit illustre la situation:
Lire
Par
construction, les cylindres ont tous la même hauteur, soit 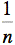 .
.
Cependant, les cylindres n'ont pas tous le même rayon.
Par contre, sachant le théorème de la relation de Pythagore applicable dans tout triangle rectangle, nous sommes en mesure de déterminer les valeurs respectives de chacun de ces rayons.
Déterminons le carré du rayon du premier cylindre (en partant du bas) de cette façon.
Déterminons le carré du rayon du deuxième cylindre.
Déterminons le carré du rayon de l'avant dernier cylindre.
Déterminons le carré du rayon du dernier cylindre.
Bref, il est
possible de déterminer la mesure des rayons des bases de chacun de ces 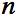 cylindres.
Par conséquent, connaissant la formule du volume d'un cylindre, nous
sommes en mesure de calculer le volume respectif de chacun de ces
cylindres.
Par conséquent, connaissant la formule du volume d'un cylindre, nous
sommes en mesure de calculer le volume respectif de chacun de ces 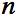 cylindres.
cylindres.
Rappelons-nous que pour un 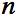 infiniment
grand, nous aurons que la somme des volumes des
infiniment
grand, nous aurons que la somme des volumes des 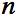 cylindres
sera égale au volume de la demie boule. Trouvons le volume de la demie
boule de rayon 1 de cette façon. Nous avons:
cylindres
sera égale au volume de la demie boule. Trouvons le volume de la demie
boule de rayon 1 de cette façon. Nous avons:
Effectuons
une mise en évidence simple du facteur 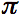 et du
facteur
et du
facteur 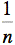 . Nous
obtenons:
. Nous
obtenons:
Remplaçons le carré des rayons de chacun des n cylindres par leur valeur respective. Nous obtenons:
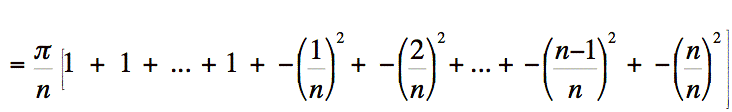
Remarquons qu'à l'intérieur des crochets, pour chaque terme de la somme des volumes des cylindres, nous avons plus 1 moins une expression, plus 1 moins une autre expression et ainsi de suite.
Nous avons une addition répétée de 1 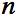 fois.
Remplaçons cette somme de 1 par son résultat qui est
fois.
Remplaçons cette somme de 1 par son résultat qui est 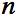 . De plus,
effectuons une mise en évidence simple du facteur -1.
. De plus,
effectuons une mise en évidence simple du facteur -1.
Alors, simplifions notre expression davantage. Nous obtenons:
Distribuons
notre facteur 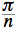 sur la différence obtenue. Nous obtenons:
sur la différence obtenue. Nous obtenons:
Simplifions. Nous obtenons:
Distribuons
notre facteur 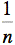 sur
la somme. Nous obtenons:
sur
la somme. Nous obtenons:
Maintenant, nous devons réfléchir sur ce que vaut l'expression ci-dessous en se ramenant à des notions que nous connaissons.
Pour
commencer, considérons le premier terme de cette somme. Cette
expression représente le volume d'un prisme dont la base est un carré
de côté 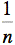 et la hauteur
est
et la hauteur
est 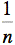 .
.
Considérons
le deuxième terme de cette somme. Cette expression représente le volume
d'un prisme dont la base est un carré de côté 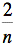 et
la hauteur est
et
la hauteur est 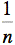 .
.
Déterminons
ce que représente l'avant dernier terme de cette somme. Cette
expression représente le volume d'un prisme dont la base est un carré
de côté 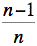 et la
hauteur est
et la
hauteur est 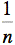 .
.
Déterminons
ce que représente le dernier terme de cette somme. Cette expression
représente le volume d'un prisme dont la base est un carré de côté 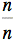 et
la hauteur est
et
la hauteur est 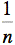 .
.
Par conséquent, l'expression mentionnée précédemment correspond à la somme des volumes des n prismes à base carrée différents.
Ces prismes
ont tous la même hauteur, soit 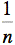 .
.
Par contre, ces prismes n'ont pas tous la même aire de base:
Le premier
c'est 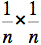 ,
,
le deuxième
c'est 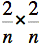
...
Et le
dernier c'est 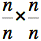 .
.
Bref,
l'aire de la base d'un prisme au suivant augmente tranquillement
jusqu'à ce que nous considérons l'aire de la base du dernier qui vaut
un unité carré. Voici une illustration de cette expression
correspondant à la somme des volumes de ces 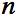 prismes.
Cela ressemble à un escalier.
prismes.
Cela ressemble à un escalier.
Remarquons que plus 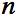 est grand, plus la représentation de cette somme aura l'allure d'une
pyramide. Plus particulièrement, pour un
est grand, plus la représentation de cette somme aura l'allure d'une
pyramide. Plus particulièrement, pour un 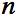 infiniment
grand, nous avons que le volume de cet escalier sera égale au volume
d'une pyramide dont l'aire de la base est
infiniment
grand, nous avons que le volume de cet escalier sera égale au volume
d'une pyramide dont l'aire de la base est 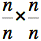 donc
d'un unité carré et la hauteur est
donc
d'un unité carré et la hauteur est 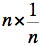 donc
d'un unité. Voici un film illustrant la situation:
donc
d'un unité. Voici un film illustrant la situation:
Lire




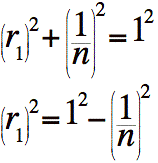

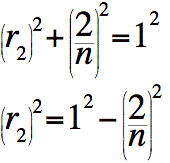

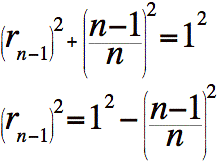

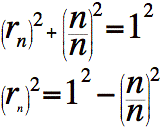

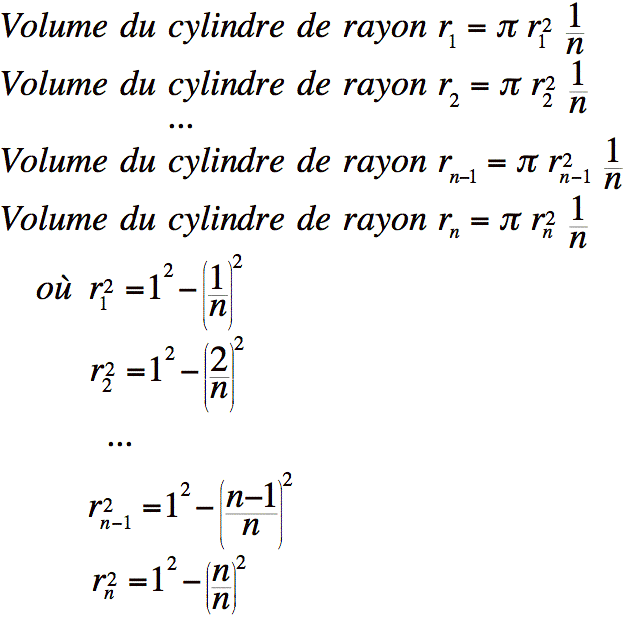
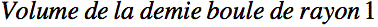
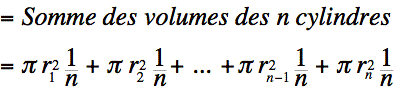
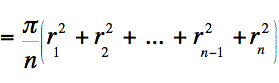
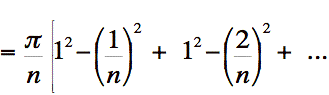
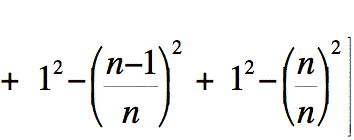
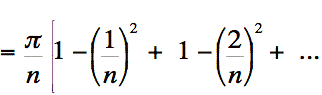
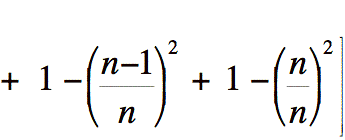
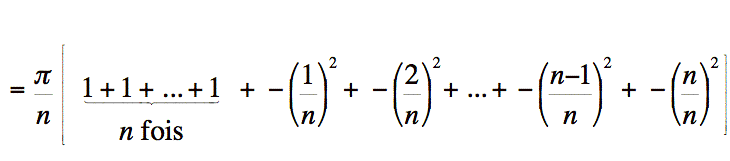
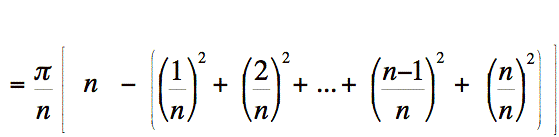
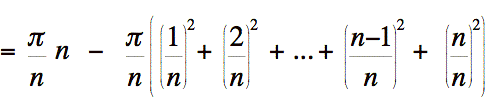
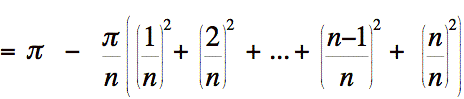
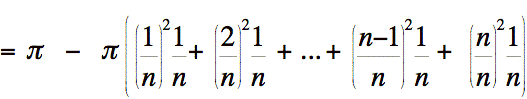
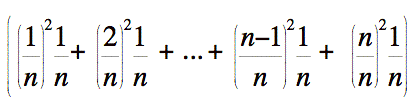
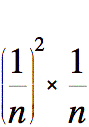
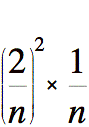
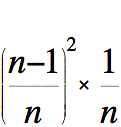
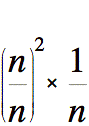


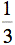 .
.