
MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Les mathématiques au Québec
Quelques points de repères



Le collège Sainte-Marie, l'ancêtre de l'UQAM

Vue aérienne du Collège Sainte-Marie

Coin Saint-Denis et Sainte-Catherine par Adrien Hébert, 1933

Université Laval à Montréal - Rue Saint-Denis - 1903

L'Université Laval (1928)

L'université McGill en 1910

Le collège de Québec fondé en 1635 (avant 1878, date de sa démolition)
La Nouvelle-France
La chaire royale de mathématiques et d'hydrographie (1678-1759)
- Jean Bourdon (1601-1668)
- Martin Boutet de Saint-Martin (1616-1683) Premier titulaire [1678]
- Jean-Baptistie-Louis Franquelin (1652-1718), [1687-1692]
- Louis Jolliet (1645-1700), [1697]
- Jean Deshayes (?-1707), [1703-1706]
- Les jésuites de Québec : 1709-1759
Le collège de Québec (fondé en 1635, fermé en 1757)
- Le programme au XVIIe siècle (Selon ce qu'on faisait en France)
Les humanités (6 ans)
-
Mathématiques pures :
- arithmétiques, algèbre, géométrie, trigonométrie rectiligne
-
Mathématiques mixtes :
- géométrie pratique : longimétrie, planimétrie, stéréométrie
- mécanique : science des forces et de l'action des corps
- hydrostatique
- astronomie sphérique (mathématiques reliées aux globes célestes)
- gnomonique
- optique : perspective, dioptrique, catoptrique
- traité de fortification (parfois)
- pyrotechnie (parfois)
Recommandations de l'Abbé Sauri : Je conseillerois encore à Messieurs les professeurs de philosophie d'enseigner mes institutions au commencement du Cours, ou du moins, d'enseigner l'Arithmétique, les quatre premières règles de l'algèbre, avec les notions de Géométrie contenue dans le n° 1, p. 141 jusqu'au n° 7 p. 147 inclusivement. Cette attention mettra leurs écoliers en état de mieux entendre la Logique et la Métaphysique. Dans la Logique même, on parle souvent de triangles, de cercles, &c. À de jeunes gens qui n'ont aucunes connoissances connoissances de ces figures; comment veut-on qu'ils entendent quelques choses aux explications du Professeur?
De la conquête (1760) à la rébellion de 1837 et à l'Union (1840)
- Le Séminaire de Québec (Thèse de 1775)
- arithmétique élémentaire,
- algèbre et de calcul des proportions suivis de problèmes d'algèbre de une à quatre inconnues,
- des énoncés sur les progressions arithmétiques et géométriques descendantes et ascendantes,
- des problèmes d'algèbre du second degré,
- des problèmes sur les alliages, les escomptes directs et inverses,
- des propositions de géométrie élémentaire (jusqu'aux triangles semblables),
- de géométrie pratique et trigonométrie.
- Le Séminaire de Québec (Thèse de 1790)
- L'Algèbre (2 propositions)
- La Géométrie (11 prop.)
- La Trigonométrie rectiligne (5 prop.) et la Trigonométrie Sphérique (8 prop.)
- Sections Coniques (1 prop.), Parabole (4 prop.), Ellipse (9 prop.), Hyperbole (8 prop.)
- Courbes Algébriques (2 prop.)
- Calcul différentiel et intégral (11 prop.)
- La Mécanique (6 prop.)
- Le jet des bombes (2 prop.)
- La Statique (3 prop.), l'Hydrostatique (4 prop.), l'Hydraulique (9 prop.), l'Optique (15 prop.), l'Astronomie (9 prop.), les Pendules (3 prop.)


- Les collèges classiques
- 1765 : Séminaire de Québec
- 1765 : Collège Saint-Raphaël, Montréal (Humanités, 1790 : ajout des classes de philosophie)
- 1803 : Collège de Nicolet
- 1811 : Séminaire de Saint-Hyacinthe
- Puis des vagues de fondations : 1830. 1846-1847 (1900, 1946 et +)

Jean-Moyse Raymond vers 1805
Étudiant au Collège Saint-Raphaël de Montréal
Musée des beaux-arts de Montréal, n° inventaire 2011.206
Classe de philosophie : nom des deux années (selon les livrets d'information) :
- 1790 : Logique : métaphisique, morale, puis Physique, mathématiques
- 1816 : Logique : métaphysique, morale, partie de mathématiques, puis Physique, mathématiques
- 1838 : Mathématiques : algèbre, géométrie, calcul différentiel et intégral, sections coniques, puis Physique, chimie.
- 8e et 7e (préparatoire) : arithmétique
- 6e et 5e : fractions ordinaires et décimales
- 4e : tenue de livre, initiation au système métrique
- 3e, 2e, 1ère : algèbre, notions élémentaires de géométrie
(Tiré de Lortie, Léon. 1955, Les mathématiques de nos ancêtres, Mémoirs de la Société Royale du Canada, t. XLIX : Troisième série, juin 1955, première section, p. 31-45.)
Pourquoi cette plus grande importance des mathématiques ?
- Fin de l'alternance des classes de philosophie (1834)
- Introduction des mathématiques dans les Humanités (1830)
- Mais au-delà :
- Besoins pratiques : pour les professions libérarles (ce n'est qu'en 1890 que la philosophie est nécessaire pour entrer dans les professions libérales)
- L'éclectisme dans l'Église catholique : connaîtres les «ismes » pour mieux les combattre
- Révolution industrielle
- Quelques hommes :
- Jérôme Demers (1765-1853) à Québec, physique, architecture, conseiller politique
- François Desaulniers à Nicolet (Va étudier à l'étranger, à l'université Georgetown près de Washington en 1833-1834), enseigne jusqu'en 1856.
- Isaac Desaulnier à Saint-Hyacinthe (Va étudier à l'étranger, à l'université Georgetown près de Washington en 1833-1834), enseigne les sciences jusqu'en 1840 (puis la philosohpie).
- John Holmes (et son voyage en Europe pour, entre
autres, équiper les laboratoires des collèges
classiques)

Costume des étudiants du Séminaire de Québec vers 1850
illustration tirée de l’album de Jacques Viger, Souvenirs Canadiens, conservé à la Bibliothèque de Montréal. 1992-508-3
Source : Michelle Boudreau-Picard, France Hervieux, Claude St-Jean, Un symbole de taille, La ceinture fléchée dans l’art canadien, Musée d’art de Joliette, 2004.


François Desaulniers, du séminaire de Nicolet
- Le mélange des élites anglaise et française : les sociétés scientifiques mixtes, la force des élites séculières.
Enseignement primaire
Enseignement classique
- classes de philosophie
- junior : philosophie (logique, métaphysique)
- sénior : philosophe (théologie naturelle et morale).
-
humanités
- Dans les années 1850 : retrait des mathématiques des
classes de seconde (belles-lettres) et rhétorique.
Les causes :
- La séparation des élites anglaise et française, à la suite de l'Union (1841) :
- vers un activisme politique des élites
- l'intérêt pour les sciences passe au second plan
- l'enseignement devient le monopole de l'église dans la société québécoise
- Auto-image des québécois francophones (après 1850) :
- Les anglais : bons en sciences et en finance
- Les canadien-français : bons dans les arts et les lettres
- L'Église catholique n'a plus d'opposants en ce qui a trait à l'éducation
- Contre les « ismes » : l'Église développe une attitude intolérante et triomphante.
- Le cours classique est vu comme le lieu de formation des élites, en particulier pour la prêtrise.
- Les sciences passe au second plan, car non nécessaire pour la formation de ces élites.
- Le latin supplante les mathématiques comme formateur de l'esprit
- L'abbé J.S. Raymond, dans son Entretien sur les études classiques, Saint-Hyacinthe, 1872 : (p. 7) Il est raconté d'un géomètre grec qu'ayant, après une longue étude, trouvé la solution d'un problème difficile et important, il allait partout s'écriant avec une expression de joie extraordinaire : Eureka : j'ai trouvé. L'élève qui voit qu'il a compris le sens de son auteur éprouve quelque chose de cette satisfaction ; il goûte du bonheur à sentir dans son intelligence assez de lumière pour pénétrer dans le secret que lui cache une langue étrangère. (...) (p. 25) Il n'y a qu'une année d'études philosophiques proprement dites : Vous savez que dans les deux dernières années du cours, les sciences physiques prennent au moins la moitié du temps. Les amis du progrès matériel ne trouveront rien à dire sans doute à l'égard des Mathématiques, de la Physique, de la Chimie. N'est-ce pas à la connaissance approfondie de ces sciences qu'est dû le mouvement matériel dont s'applaudit notre siècle ? Ceci est trop évident pour être contesté.
- L'abbé L.A. Paquet, L'Église et l'éducation à la lumièe de l'hsitoire et des principes chrétien, 1909 : Or l'expérience de je ne sais combien de siècles a constaté et enseigné qu'il n'y a rien comme l'étude des langues classiques pour développer et mûrir les facultés de l'esprit des jeunes gens. La version grecque et la version latine captivent toutes leurs facultés, les astreignent à la réflexion, à la discussion d'un texte, pendant des jours, sans distraction possible, avec l'ambition de trouver et la satisfaction d'avoir trouvé par eux-mêmes un sens et le vrai sens ; ce que ne saurait faire aucune étude pratique, sauf peut-être les mathématiques qui deviendraient desséchantes au possible si elles étaient seules.
- La fondation de la Faculté des arts de
l'Université Laval (après 1852) : Un nivellement par le
bas dans les collèges classiques, pour que tous les
collèges de la provinces aient des programmes
similaires.
- Pourtant, des hommes ayant une formation scientifique occupent des postes importants dans la hiérarchie de l'Église et de l'éducation :
- Mgr Thomas-Étienne Hamel (1830-1913), deuxième recteur de l'Université Laval, premier québécois à obtenir une licence en science, de l'École de Carmes à Paris, en 1853.
- Voici ce que dit de lui D. Gosselin (Les étapes d'une classe au Petit Séminaire de Québec, 1859-1868, Québec, 1908) à propos de son enseignement de la classe de Philosophie junior en 1866-1867 : Il lui manqua le temps de remanier le cours qu'il avait suivi à Paris, de l'adapter à un autre milieu, d'en réduire les proportions, de le mettre à la portée d'étudiants dont plusieurs ne savaient presque rien, même en arithmétique. L'heure du cours quotidien se passait à copier - à toute vapeur - ce que l'on nous dictait. Sous le titre de "théorie des limites", incompris du grand nombre, il me souvient d'avoir grifonner quatre cent lignes d'une écriture fine et serrée. Le temps libre qui suivait chaque cours suffisait à peine à réviser et à corriger les pages manuscrites. Le moulin à problème, il nous forçait rarement à le tourner, se contentant de nous livrer les formules sans lesquelles, il ne pouvait être mis en mouvement. Ces opérations qui ne sont que l'application des principes, et avec lesquelles il importe de se familiariser, elles étaient laissées à l'initiative de chacun. De plus, l'arithmétique eut la part du lion, près de six mois sur dix. Il en restait à peine quatre pour l'algèbre, la géométrie et la trigonométrie. Cette dernière, nous ne pûmes la voir qu'à vol d'oiseau. La résultante, facile à prévoir, fut peu consolonate pour le professeur, peu glorieuse pour les élèves. (...) Bien peu mordaient aux mathématiques, il serait puéril de le nier, et nous avons suivi ce cours plutôt en amateurs.
- Mgr Jean Langevin (1821-1892) , professeur au Séminaire de Québec (1838) , premier principal de l'École normale Laval et premier évêque de Rimouski, auteur présumé du premier livre de calcul différentiel et intégral publié au Canada : Traité élémentaire de Calul différentiel et intégral, 1848.


Un original : Charles Baillairgé (1827-1906)
- Premier auteur canadien français vraiment original en mathématiques
- Nouveau traité de géométrie et de trigonométrie rectiligne et sphérique, suivi du toisé des surfaces et des volumes et accompagné de tables de logarithmes des nombres et sinus etc. naturels et logarithmiques et d'autres tables utiles. Ouvrage théorique et pratique illusré de plus de 600 vignettes, avec un grand nombre d'exemples et de problèmes à l'usage des Arpenteurs, Achitectes, Ingénieurs, Professeurs et élèves, etc. , Québec, 1866. (un livre de 900 pages)



Le XXe siècle
Les universités
- L'université McGill 1821
- Prend son envol après 1850-1860
- Les bienfaiteurs : Molson, Redpath, Macdonald, etc.
- Les premiers grands scientifiques : Dawson (Géologie), Osler (Étude des plaquettes sanguines), Rutherford (Modèle atomique).
- Faculté de génie reconnue après 1870.
- Université reconnue pour ses recherches, après 1890.
- L'Université Laval 1852
- Quatre facultés au départ : Théologie, médecine, droit, arts (collèges classiques).
- Succursale de Montréal : 1876 (premier étudiant en 1878)
- École polytechnique de Montréal 1873 (ouvert en 1874)
- La saga de la fondation de l'École polytechnique
- Demandée au gouvernement par des montréalais en 1870
- Offerte à l'Université Laval, mais refusée par celle-ci, en 1872
- Accpetée en 1873 par la CECM (maintenant CSDM) par Urgel Archambeault, le directeur de l'Académie commerciale catholique de Montréal.
- Devient l'École polytechnique en 1876.



- 114 diplômés en 25 ans (1877-1904) soit 4,56 par année.
- De ces diplômés, seulement 54 provenaient de collèges classiques.
- Professeurs :
- Victor-Elzéar Beaupré (1882-1974), premier actuaire canadien français
- Conrad Manseau (1882-1958) (Astronomie Sorbonne 1914)
- Arthur Pelletier (1870-1945), professeur 1913-1940. 256 problèmes dans le Mathematical Monthly.
- L'École des hautes études commerciales (1906)
- Premiers étudiants : 1910 (30 étudiants, il en reste 19 l'année suivante)
- 1915 affiliation à l'Université Laval à Montréal

- L'Université de Montréal et sa Faculté des sciences
- Écoles techniques
- Institut de technologie de Montréal (1907)

En 1915
- Faculté des sciences fondée en 1919-1920.
- Soutien essentiel de la Fondation Rockfeller pour créer la Faculté de médecine.
- Exige une meilleure formation scientifique
des étudiants : d'où création de la Faculté des
sciences, qui devient un point d'entrer en
médecine.
- Système de certificats (comme en France)
- 1920 : 50 en P.C.N. et 10 ailleurs
- Premier professeur de mathématiques : Arthur Léveillé (B.A. honor in mathematics, U. of London, décédé en 1947)
- De 1920 à 1940 : 8 licences en mathématiques.
- 1936, un premier diplômé, Abel Gauthier, entreprend des études graduées (à Columbia, M.Sc, 1938). Il sera directeur de 1947 à 1957, succédé par Maurice Labbé.
- Le frère Robert (F.I.C.) : Premier diplômé en mathématiques,1938, à obtenir, en 6 mois, un doctorat de l'université de Lille (1ière thèse : Soleil, étoile variable, 2ième thèse : Les fonctions presque périodiques.) Auteurs de nombreux manuels de mathématiques dans les années 40.

- 1920-1960 : La polémique sur l'enseignement des sciences au secondaire
- Université Laval
- Fondation de la Faculté des sciences en 1937
- 1939 : création et organisation du département de mathématiques par Adrien Pouliot.


Adrien Pouliot (1896-1980) Maurice Labbé (1920-2006)
- Polémique autour de l'enseignement des sciences
au Québec (1920 +)
- UQAM : fondation en 1969
- Évolution du nombre d'étudiants en mathématiques dans les universités québécoises
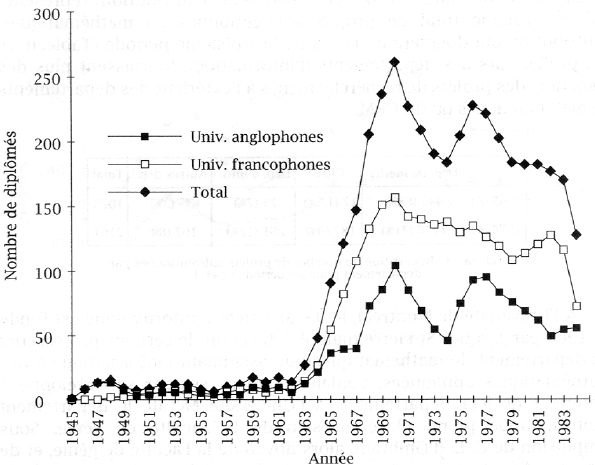
- Les mathématiques modernes au secondaire, dans la foulée
du Rapport Parent.
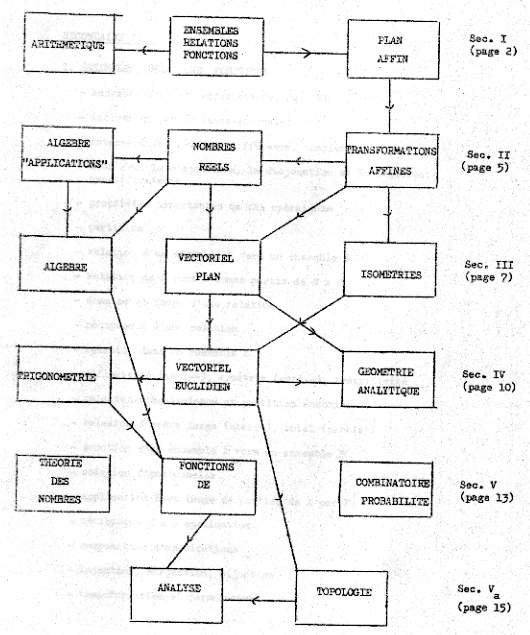
Mathématiques, Projet de programme moderne (Secondaire I à V), Première version, préparée par Jacques Bordier et Pierre DeCelles, Ministère de l'Éducation, division de la Mathématique, Québec, janvier 1969.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |