
MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Géométrie des transformations
et les « mathématiques modernes »
Géométrie des transformations
-
Au-delà de la géométrie euclidienne (déductive et synthétique)
(inspiré de Amy Dahan-Dalmedico, Jeanne Peiffer, Histoire des mathématiques, Routes et dédales, Paris : Éditions du Seuil (coll. Points, S49, 1986, chap. 4)- Euclide : la seule transformation explicite est le déplacement des figures utilisées dans ses démonstrations.
- La perspective et après...
- Brunelleschi (1377-1446), le
premier
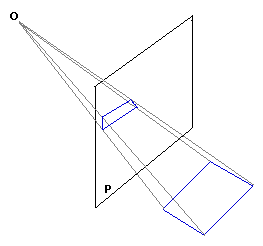 à avoir expliciter les règles de la perspective.
à avoir expliciter les règles de la perspective.
- Dürer en 1525 et Piero della Francesca en 1470 précisent ces règles mais toujours sans fondement mathématiques clairs.
- Leone B. Alberti, en 1511, cherche à répondre à la question : « Quelles sont les propriétés géométriques communes à deux perspectives d'une même figure.
- La cartographie amène à s'intéresser aux projections de la sphère dans un plan. En particulier, on remarque que de telles projections ne peuvent conserver les angles. On se rabat sur la conservation des longueurs. Après 1600, essor de l'étude des projections. La publication de plusieurs éditions des Sections coniques d'Apollonius donne de nouveaux outils mathématiques. Kepler, dans son Astronomia Nova (1609), utilise ces connaissances pour ses calculs débouchant sur sa première loi du mouvement des planètes, à savoir que les planètes ont une orbite elliptique.
- Girard Desargues (1591-1661)
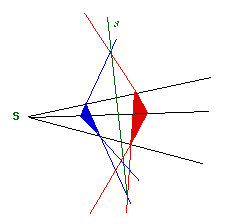 Brouillon
projet d,une atteinte aux événements des
rencontres d'un cône avec un plan (1639)
(50 copies seulement furent imprimés)
Brouillon
projet d,une atteinte aux événements des
rencontres d'un cône avec un plan (1639)
(50 copies seulement furent imprimés)
- Les coniques sont vues comme des projections d'un cercle dans un plan.
- Théorème de Desargues : Si deux triangles, situés dans l'espace ou dans un même plan, ont leurs sommets placés deux à deux sur trois droites concourant en un même point, leurs côtés se rencontrent, deux à deux, en trois points situés en ligne droite, et réciproquement.
- Certaines des propriétés du cercle sont transférés aux coniques par le fait que la projection n'altère pas ces propriétés.
- Notion d'invariant. Quelles sont les propriétés qui sont invariantes par projection ?
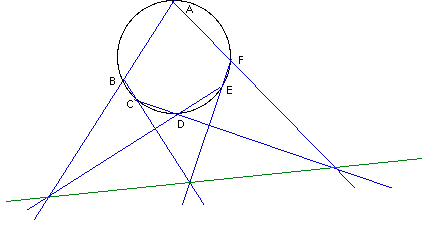
- Blaise Pascal (1623-1662) Essai sur les coniques (1640)
Si ABCDEF est un hexagone inscrit dans une conique, alors, les points de rencontre des trois couples de côtés opposés AB et DE, BC et EF, CD et FA sont en ligne droite.
- Brunelleschi (1377-1446), le
premier
- Jean-Victor Poncelet (1788-1867) Traité
des propriétés projectives des figures (1822)
Composé dans les prisons russes après la défaite de Napoléon en Russie.Son programme : Trouver les propriétés géométriques communes aux sections planes de diverses projections.
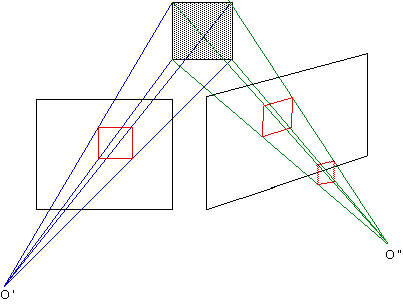
Figures homologiques
Exemples de propriétés invariantes par projection : alignement, droites concourantes, le Théorème de Pascal. Les transformations du plan dans le plan se placent au coeur de son travail.
- Influence de Poncelet : chez Möbius
(1790-1868), Plücker (1801-1868) et Michel Chasles
(1793-1880)
Les transformations géométriques
Möbius et Chasles traduisent en termes analytiques l'idée de transformation de Poncelet. En particulier, Möbius met en évidence la notion de transformations affines, c'est-à-dire celles qui conservent le parallélisme sans nécessairement conserver les distances. Il y a deux types de transformations affines, les déplacements (qui ne modifie pas le figure en tant que telle (rotations, translation, symétrie et rotation, selon Euler) et les similitudes.
- Multiplication des géométries De 1792
à 1870
GéométrieTerminologie de KleinNombre de parallèles par un point à une droite donnéesSomme des angles d'un triangleEuclideGéométrie paraboliqueune parallèlePiGauss - Bolyai - Lobatchevskygéométrie hyperboliqueun infinité de parallèlesinférieure à PiRiemanngéométrie elliptiquepas de parallèlessupérieure à Pi- Félix Klein (1849-1925).
- Il montre que la géométrie euclidienne, et toutes les géométries métriques, sont un cas particulier de la géométrie projective.
- Considérations comparatives sur
les recherches géométriques modernes
(1872)
- Il remarque que les différentes géométries peuvent se caractériser par l'ensemble des transformations qui gardent invariants certaines propriétés (exprimés en fait par des formes algébriques homogènes). Ces ensembles constituent des groupes, c'est-à-dire que la composition de deux transformations de cet ensemble est dans cet ensemble, et qu'il y a une transformation identité et chaque transformation a un inverse. Un exemple d'un tel groupe : le groupe des rotations.
GroupePositionDirectionOrientationDistanceAngleParallélismeIdentitéXXXXXXTranslation
XXXXXDéplacements
XXXXIsométrie
XXXSimilitudes
XX- La géométrie elliptique correspond au groupe transformations qui laissent invariante une ellipsoïde imaginaire.
- C'est une vue très unificatrice : unification des géométries mais aussi avec l'algèbre par le fait que certaines formes algébriques forment des groupes équivalents (isomorphes) à certains groupes de transformations et donc à leur géométrie. Les géométrie non-euclidiennes qui ébranlaient auparavant l'édifice mathématiques en viennent à se rattacher elle.
- David Hilbert (1862-1943) Fondements de la géométrie (1899)
Les discussions sur la nature de la géométrie et sur la nature des objets géométriques a relancé le débat sur les définitions qui devraientà la base de la géométrie. Hilbert entreprend donc donner une nouvelle axiomatisation de la géométrie. Dans celle-ci, les objets ne sont pas définis par leur nature mais plutôt par les propriétés des relations que ces objets ont entre eux.
Ce système d'axiomes doit être consistant (il n'entraîne aucune contradiction) et indépendant (aucun axiome ne peut découler des autres). Plus tard on ajoutera une autre exigence, soit que le système soit complet (un énoncé ne peut être que vrai ou faux).
L'école allemande qui développera à partir de là sera très influente dans le monde. La mathématique axiomatique deviendra dans les décennies à venir la principale forme de mathématiques.
- Nicolas Bourbaki
[ Bourbaki, Une société secrète de mathématiciens, Pour la Sciences, Les génies de la science, n° 2, fév- mai 2000.]- Nom que s'est donné un groupe de mathématiciens, principalement français, qui a commencé à se réunir dans les années 1930. À partir de 1939, le groupe a publié des fascicule de leur oeuvre, les Éléments de mathématiques qui se voulait une une approche axiomatique systématique pour reconstruire toutes les mathématiques.
- La publication ces fascicules a été particulièrement soutenue dans les années 1950.
- Les Éléments de mathématiques devait se diviser en six section : Théorie des ensembles, Algèbre, Topologie générale, Fonctions d'une variable réelle, Espaces vectoriels topologiques, Intégration.(D'autres sujets ont aussi été abordés)
- Le but premier était d'écrire un Cours d'analyse qui prendrait en compte les fondements des mathématiques. S'inspirant du Algèbre moderne de van der Waerden, ils voulaient trouver un ensemble d'axiomes sur lesquels construire leur édifice mathématique.
- La rédaction d'un fascicule prenait de 10 à 12 ans. Le mode de rédaction était le suivant : Première rédaction, séminaire de "démolition", deuxième rédaction par un nouveau rédacteur, nouveau séminaire de "démolition", etc. jusqu'à ce qu'il y a un consensus pour dire que le fascicule est prêt pour la publication.
- L'oeuvre de Bourbaki est totalement déductive.
- L'influence de Bourbaki : Les mathématiques modernes : un enseignement basé sur une approche ensembliste et un vision axiomatique des mathématiques.
- Bourbaki et la réforme de l'enseignement
des mathématiques au début des années 1960.
- Prépondérence de la pensée bourbakiste (concepts unificateurs) dans les milieux mathématiques
- Besoin de réforme des mathématiques suite au lancement du premier spoutnik. (1958)
- En géométrie,comme ailleurs en mathématiques, il faut partir de concepts unificateurs. La géométrie des transformations est un paradigme bourbakiste de concept unificateur.
- La géométrie euclidienne étant une partie de la géométrie projective, vue par l'intermédiaire des groupes de transformations, elle sera déplacée dans les programmes du secondaire dans les années 1960 par la géométrie des transformations. « À bas Euclide ! » Ce n'est que maintenant qu'Euclide refait surface.
______________________________________________________________________________________________
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |