MAT 6221

Bas de la page

Montrons que crd²(a/2) = R(2R - crd(180° - a)) (esquisse)

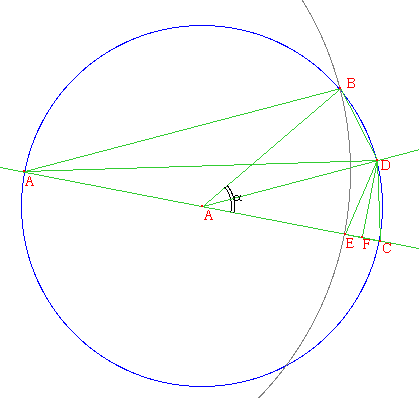Sur la figure ci-contre, crd(a) est le segment BC(non tracé), et crd (a/2) est le segment DC. Le segment AD est correspond donc à la bissectrice de l'angle a (noté alpha sur la figure).

Le point E est l'intersection de AC et du cercle de centre A' (le A sur le cercle dans la figure) passant par B.

Remarquons les congruences suivantes :

Le triangle ABD est congruent au triangle ACD (par congruence C_A_C). On a donc BD = CD. Or on a aussi que BD = DE, car A'BD et A'ED sont congruents (C_A_C). Donc DC = ED.

En prenant F, la projection orthogonale de D sur A'C, on a que EF = FC, puisque le triangle EDC est isocèle. Ainsi, 2CF = (A'C - AE) = (A'C - AB) = 2R - crd(180 - a).

De plus, on a que les triangles A'CD et DCF sont semblables, par le cas de similitude A_A_A_. Dès lors, on a A'C / CD = CD / CF. On a donc

crd²(a/2) = CD² = AC x CF = 2R x( (2R - crd(180 - a)) / 2)

= R x (2R - crd(180 - a))

Haut de la page