Généralisation à trois dimensions
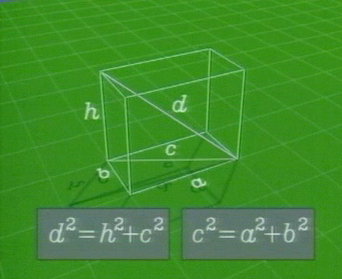
Dans la situation décrite par le graphique ci-dessous,
il suffit d'appliquer deux fois le théorème de Pythagore (à deux dimensions)
pour obtenir $d^2=a^2+b^2+h^2$.
Réciproque du théorème de Pythagore
Si, dans un triangle de côtés a, b et c on a $a^2+b^2=c^2$, alors l'angle opposé au côté c est droit. Cet énoncé découlera de la loi du cosinus, étudié à la page suivante.
Autre preuve du théorème de Pythagore, et même un peu plus
L'argument ci-dessous utilise les triangles semblables pour démontrer le théorème de Pythagore,
en notant au passage que les surfaces de même couleur ont même aire.
On pourra aussi obtenir le même résultat via les aires, comme cas particulier
de la loi du cosinus (page suivante).

Comme les triangles ABC et CBH sont semblables, on obtient
${c \over a} = {a \over c_1}$, et donc $cc_1 = a^2$.
De même, puisque les triangles ABC et ACH sont semblables, on obtient
${c \over b} = {b \over c_2}$, et donc $cc_2 = b^2$.
On a donc : $c^2 = c(c_1+c_2) = cc_1+cc_2 = a^2+b^2$.