« Existe-t-il un lien entre l'aire des polygones réguliers et l'aire du cercle de même rayon ? »
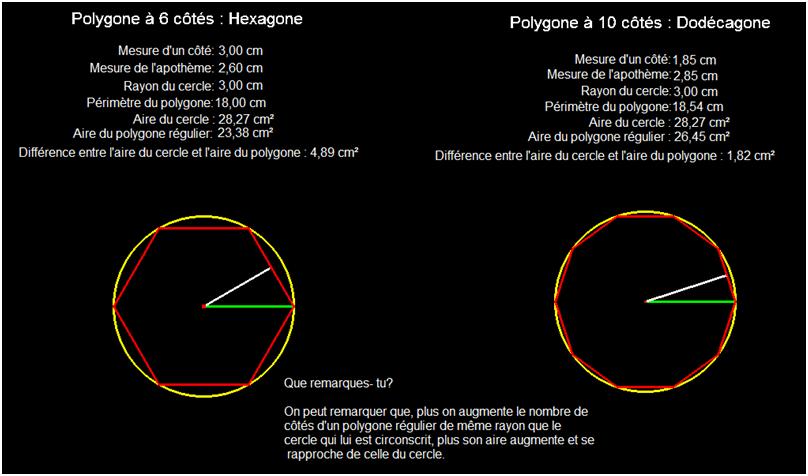
Observons la différencre entre l'aire d'un polygone régulier et celle du cercle ayant le même rayon.
Observons la différencre entre l'aire d'un polygone régulier et celle du cercle ayant le même rayon.
Parlons maintenant un peu « formules » !!!
Si n est le nombre de côtés du polygone, son aire est toujours donnée par la formule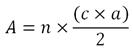 , où « n x c » correspond au périmètre du polygone.
, où « n x c » correspond au périmètre du polygone.
De ce fait, l’aire du polygone peut être donnée par la formule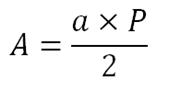 , où P représente le périmètre du polygone.
, où P représente le périmètre du polygone.
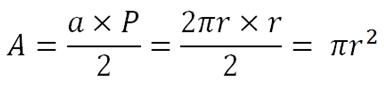 .
.

Si n est le nombre de côtés du polygone, son aire est toujours donnée par la formule
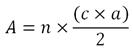 , où « n x c » correspond au périmètre du polygone.
, où « n x c » correspond au périmètre du polygone. De ce fait, l’aire du polygone peut être donnée par la formule
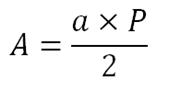 , où P représente le périmètre du polygone.
, où P représente le périmètre du polygone. Si on augmente de
plus en plus le nombre de côtés du polygone, son aire se rapproche de celle du disque.
On peut donc affirmer que, dans le cas d'un polygone ayant un très grand nombre de côtés, le périmètre du polygone deviendra la circonférence
du cercle de même rayon, soit le cercle circonscrit, et que l’apothème du polygone deviendra le rayon de ce cercle.
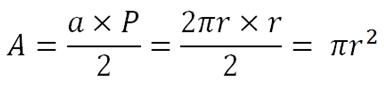 .
.
© Copyright 2008 Colorus design
Design
by Reality
Software