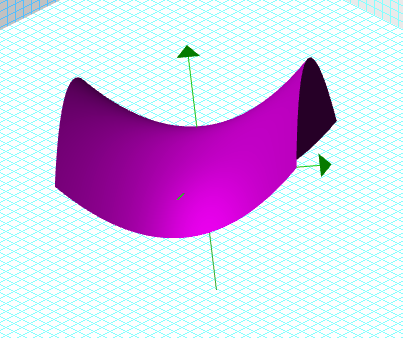
Les Quadriques
E-E-E
Description
La quadrique que nous avons nommé E-E-E ou Elipse-elipse-elipse est en
fait nommée ellipsoïde. Cette surface et son intersection avec chacun
des plan des trois dimensions nous permet d'obtenir une ellipse.
L'ellipsoïde est généralement utilisée lorsqu'on fait l'étude de la
mécanique des fluites.
Il existe un cas particulier de l'éllipsoïde qui est l'ellipsoïde de révolution. Ce type d'éllipsoïde est créé par la rotation d'un éllipse sur un de ses axe. Ce type d'ellipsoïde a ;a forme d'un ballon de rugby est décrit la forme optimale d'un ballon dirigeable.
Finalement, il existe un cas particulier de l'ellipsoïde de révolution qui est la sphère.
Il existe un cas particulier de l'éllipsoïde qui est l'ellipsoïde de révolution. Ce type d'éllipsoïde est créé par la rotation d'un éllipse sur un de ses axe. Ce type d'ellipsoïde a ;a forme d'un ballon de rugby est décrit la forme optimale d'un ballon dirigeable.
Finalement, il existe un cas particulier de l'ellipsoïde de révolution qui est la sphère.
Graphing Calculator
Pour la réalisation de la représentation dans graphing calculator, nous avons fixé les paramètres de la forme canonique.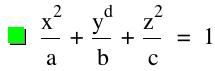
a=2, b=1, c=0,5 et d=2
Voici alors la quadrique obtenue:

Films:
En utilisant les mêmes valeurs pour les paramètres, nous avons aussi
produit différents films qui représentent la quadrique sous différents
plans et les coniques obtenues lorsqu'on coupe la quadrique avec un
plan.
Quadrique
Intersection avec plan XY
On voit très bien que l'intersection de la quadrique avec le plan décrit une ellipse.
Intersection avec plan XZ
On voit encore très bien l'ellipse.
Intersection avec plan YZ
Encore une ellipse.
