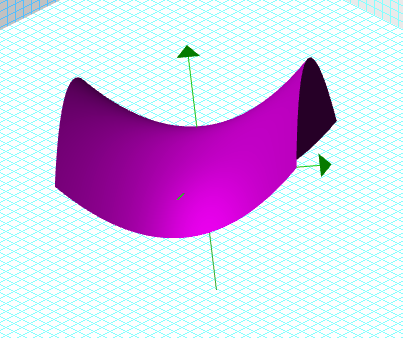
Les Quadriques

Description

Il existe différents cas de quadriques. Nous les avons classés selon les coniques obtenues en faisant des coupes subséquentes de plans. Selon ce point de vue, nous avons trouvé alors que nous obtiendrions 10 quadriques différentes, soit les suivantes:

Majoritairement ellipse:

Ellipse-Ellipse-Ellipse
Ellipse-Ellipse-Parabole
Ellipse-Ellipse-Hyperbole

Majoritairement Parabole:

Parabole-Parabole-Parabole
Parabole-Parabole-Ellipse
Parabole-Parabole-Hyperbole

Majoritairement Hyperbole:

Hyperbole-Hyperbole-Hyperbole
Hyperbole-Hyperbole-Parabole
Hyperbole-Hyperbole-Ellipse

Mixte:

Hyperbole-Ellipse-Parabole

Cependant, lors de nos expérimentations avec graphing calculator et MégaPov, nous avons vite réalisé que nous n'avions que 4 cas généraux de quadriques. Voici les raisons qui nous ont poussés à ces conclusions:

Toujours en nous basant sur l'écriture canonique:

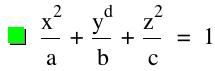
Afin de faire apparaître une hyperbole, nous devons avoir a, b ou c négatifs. Dans cet exemple, prenons a<0, b>0, c>0 et d=2. Dans ce cas, nous obtenons une ellipse en fixant le terme en x et une hyperbole en fixant le terme en y ou en z. Nous avons alors conclu que les hyperboles doivent nécessairement venir en paires si elles sont construites avec une ellipse.

D'autre part, si on veut obtenir une parabole, nous devons nécessairement en avoir deux, car en réduisant la puissance d'un terme, ont créé nécessairement deux paraboles.

Voici alors les cas généraux des quadriques:
Ellipse-ellipse-ellipse
Ellipse-parabole-parabole
Ellipse-hyperbole-hyperbole
Hyperbole-parabole-parabole