Les Quadriques
E-H-H
Description
La
quadrique que nous nommons E-H-H ou Ellipse-Hyperbole-Hyperbole se
nomme en fait hyperboloïde. Il existe deux cas d'hyperboloïdes:
l'hyperboloïde à une nappe et l'hyperboloïde à deux nappes.
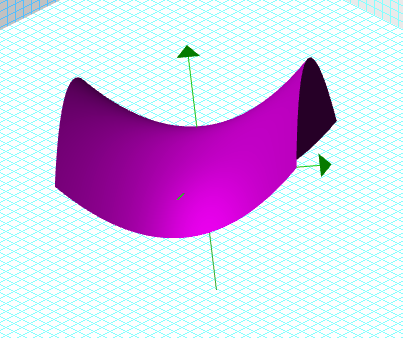
L'hyperboloïde à une nappe, dans le cas où elle est formée par une
rotation d'une hyperbole, est le cas le plus répendu car on retrouve
cette quadrique en architecture. Sa construction peut être accomplie à
l'aide de poutres rectilignes qui en font une structure très solide.
Pour l'hyperboloïde à deux nappes, on peut voir sa construction comme étant la rotation d'une hyperbole autour de l'axe qui relie ses foyers. Ceci décrit seulement un cas de l'hyperboloïde, si on imagine la rotation se faisant sur une ellipse, on obtient alors le cas général.
Pour l'hyperboloïde à deux nappes, on peut voir sa construction comme étant la rotation d'une hyperbole autour de l'axe qui relie ses foyers. Ceci décrit seulement un cas de l'hyperboloïde, si on imagine la rotation se faisant sur une ellipse, on obtient alors le cas général.
Graphing Calculator
Pour la réalisation de la représentation dans graphing calculator, nous avons fixé les paramètres de la forme canonique.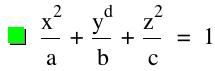
a=2, b=1, c=-2 et d=2
Voici alors la quadrique obtenue pour l'hyperboloïde à une nappe:

Films:
En utilisant les mêmes
valeurs pour les paramètres, nous avons aussi
produit différents films qui représentent la quadrique sous différents
plans et les coniques obtenues lorsqu'on coupe la quadrique avec un
plan.
Pour ce cas de quadrique, nous avons fait deux séries de films, une série pour l'hyperboloïde à une nappe et une pour l'hyperboloïde à deux nappes:
Pour ce cas de quadrique, nous avons fait deux séries de films, une série pour l'hyperboloïde à une nappe et une pour l'hyperboloïde à deux nappes:
Quadrique
Hyperboloïde à deux nappes:
Hyperboloïde à une nappe:
