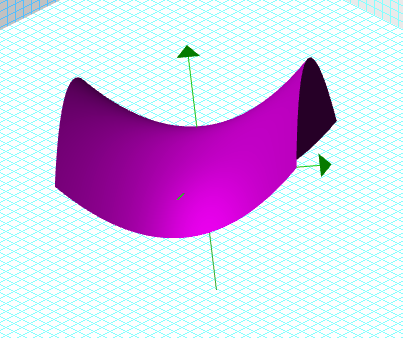
Les Quadriques
E-P-P
Description
La
quadrique E-P-P ou Ellipse-Parabole-Parabole se nomme en fait le paraboloïde
elliptique. Elle est regroupée avec l'autre paraboloïde, soit le paraboloïde
hyperbolique. Pour ce cas de paraboloïde, les coupes avec chacun des plans,
lorsque la surface est droite, dessine une parabole sur deux plans et une
ellipse sur l'autre.
Comme pour la majorité les quadriques, il existe un paraboloïde de révolution que
l'on obtient en faisant la rotation d'une parabole atour de l'axe passant par
le foyer et le sommet de la parabole. La quadrique ainsi obtenue est la
parfaite représentation d'une antenne parabolique.
Finalement,
dans la mécanique des fluides, un liquide qui tourne dans un cylindre formera
un paraboloïde de révolution.
Graphing Calculator
Pour la réalisation de la représentation dans graphing calculator, nous avons fixé les paramètres de la forme canonique.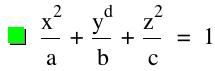
a=2, b=1, c=0,5 et d=1
Voici alors la quadrique obtenue:

Films:
En utilisant les mêmes valeurs pour les paramètres, nous avons aussi
produit différents films qui représentent la quadrique sous différents
plans et les coniques obtenues lorsqu'on coupe la quadrique avec un
plan.
