Les Quadriques
H-P-P
Description
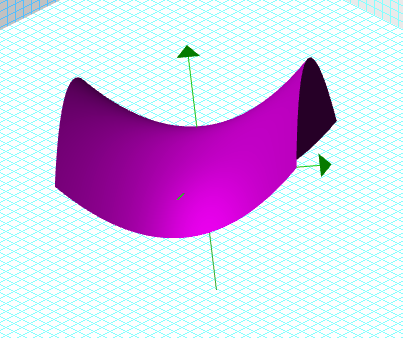
La
quadrique H-P-P ou Hyperbole-Parabole-Parabole se nomme paraboloïde
hyperbolique. Dans un autre système de classification, il est regroupé
avec l’autre
paraboloïde, le paraboloïde elliptique. Pour ce cas de paraboloïde,
deux des
coupes avec des plans donnent des paraboles alors que la dernière,
donne une
hyperbole.
Cette
quadrique, comme l’hyperboloïde à une nappe, est une surface qui peut
être
construite à l’aide de droite, ainsi, on retrouve beaucoup d’exemples
d’hyperboloïdes
à une nappe en architecture, comme dans le cas d’un toit en selle. Le
nom de ce
type de toit découle directement de la forme que prends l’hyperboloïde,
soit
celle d’une selle à cheval. Finalement, on retrouve un autre exemple de
l’hyperboloïde
en les croustilles de la marque Pringles.
Graphing Calculator
Pour la réalisation de la représentation dans graphing calculator, nous avons fixé les paramètres de la forme canonique.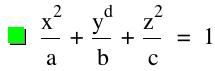
a=2, b=1, c=-0,5 et d=1
Voici alors la quadrique obtenue:

