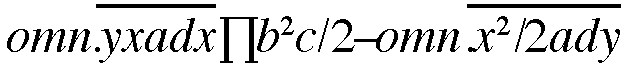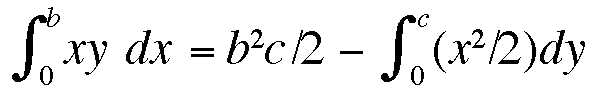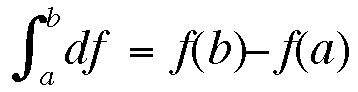MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Cours
(Ce qui suit est basé sur les quatre derniers articles de
Jacques Lefebvre)
Isaac Newton
(1642-1727)
Les trois approches de Newton :
(Ce qui suit est basé sur les quatre derniers articles de Jacques Lefebvre)
Isaac Newton
(1642-1727)
Les trois approches de Newton :
- Les méthodes des infinitésimaux (écrit 1669,
publié en 1711)
Si y = xn, alors y' = ((x+o)n - xn)/o = (xn + nxn-1o + (n(n-1)/2!) xn-2o2 + … - xn)/o = nxn-1(o/o) + (n(n-1)/2!) xn-2o + …
= nxn-1 - La méthode des fluxions (Méthode
des fluxions et des suites infinies, écrit 1671, publié
????, en anglais, 1740 en français)
Si y = xn, alors y'(on devrait écrire y avec un point par dessus) est la fluxion de la fluente y, et x' est la fluxion de la fluente x. Les accroissements respectifs de y et x sont x'o et y'o. Calcul de y'.
y + y'o = (x + x'o)n = xn + nxn-1x'o + (n(n-1)/2!) xn-2(x'o)2 + … .
- La méthode des première et dernières raisons.
(Principia Mathematica, 1687)
La dérivée est (y(x+h) - y(x))) / h, lorsque h devient aussi petit que l'on veut.
Donc y' = nxn-1x' + (n(n-1)/2!) xn-2x'2o + … = nxn-1x' .
 Le
théorème fondamental du calcul
Le
théorème fondamental du calcul
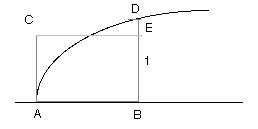
Si z est la surface sous la courbe à B, DB : BE :: z' : x'
où BE = 1, donc z' = x' DB.
Gottfried Wilhelm Leibniz
(1646-1716)
Trois idées qui l'ont inspirées.
- Mettre en place un véritable calcul
- La technique des suites
- La généralisation du triangle caractéristique
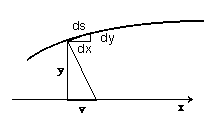 Dans
la figure, on a dy/v = dx/y, ou vdx = ydy. Ce qui permet
de trouver l'aire formée par les sous-normales (v).
Dans
la figure, on a dy/v = dx/y, ou vdx = ydy. Ce qui permet
de trouver l'aire formée par les sous-normales (v).
La recherche d'une notation fonctionnelle qui dirige la pensée.
signifie
Voir aussi le cours 8 : l'origine de la notation pour la dérivée seconde.
Basé sur l'égalité a1 - an = (a1 - a2) + (a2 - a3) + … + (an-1 - an)
Il en tire que la somme infinie des nombres de la forme an = 1/n(n+1) est 1. (Exercice : à montrer)
Il en tire aussi que la somme des différences égale la différence des valeurs extrêmes de la fonctions, soit
Publications :
1684 Le calcul différentiel, mais avec des définitions boiteuses.
Tangente : une droite sécantes dont les points d'intersectionà la courbes sont très (indéfiniment ?) proches.
1686 Le calcul intégral
Les réponses aux objections
- 1689 : dx est un grain de sable par rapport la Terre
- 1694 : Multiplier un infiniment infini par dx donnera x (un avant goût des infinis de divers ordre de Canot)
- vers 1700 : Penser en termes d'indéfiniment grands, donc d'infini potentiel.
Mais il y a des incongruités
- Ce qui est vrai pour P(x) lorsque x s'approche d'une valeur xo, l'est aussi à la valeur xo
- La somme 1 - 1 + 1 - 1 + 1 - … = 1/2 (la moyenne entre la somme d'un nombre pair de 1 et celle d'un nombre impair de 1)
Marquis de l'Hospital : Analyse des infiniment petits, Pour l'intelligence des lignes courbes (1696)
- Première publication structurée du calcul différentiel de Leibniz
- Définitions plus ou moins claires des éléments de base : quantités variables, quantités constantes, différences, différentielles
- Deux demandes
- x + dx = x
- Une courbe « peut être considérée comme l'assemblage d'une infinité de lignes droites, chacune infiniment petite (…) ».
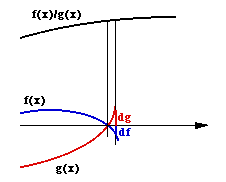 Les
règles de manipulation des différences
Les
règles de manipulation des différences
- d(xy) = (x+dx)(y+dy) - xy = xy + xdy + ydx + dxdy -xy = xdy + ydx + dxdy = xdy + ydx.
- On en tire d(xn) = nxn-1, en posant y = x dans la règle précédente et en augmentant le nombre de variable.
- La règle de l'Hospital (article 163)
Autour du point où f(x) et g(x) s'annulent en même temps, le rapport f(x)/g(x) est le même que le rapport df/dg (en regardant le tout en valeur absolue)
Le XVIIIe siècle - le siècle du formalisme, puis celui des remises en question
Le siècle d'Euler
Leonard Euler (1707-1783)
- Introduction in analysin infinitorum (1748), Institutiones calculi differentialis (1755), Institutiones calculi integralis (1768-1770).
- Le calcul formel
Premier exemple
Puisque a0 = 1, Euler pose ai = 1 + ki, où i est infiniment petit. Pour tout nombre x fini, il existe un infiniment grand tel que N = x/i, d'où
ax = (1 + (kx/N))N.
En utilisant le développement du binôme, et considérant que 1 = (N-1)/N = (N-2)/N = … , Euler obtient
ax = 1 + kx/1! + k2x2/2! + … ,
et en désignant a par e, le nombre népérien, ou d'Euler, avec k = 1, on obtient
ex = 1 + x/1! + x2/2! + … , et donc e = 1 + 1/1! + 1/2! + … .
Second exemple
1/(1+1)2 = 1/4, entraîne que 1 - 2 + 3 - 4 + 5 = 1/4, car 1/(1+1)2 = 1 - 2x + 3x2 - 4x3 + …
Les réactions au manque de fondement du calcul
Berkeley (1685-1753)
- Obscurité des concepts
- Non-validité des méthodes
Colin Maclaurin
- Le retour aux grecs.
Jean le Rond d'Alembert (1717-1783)
- Vers la limite comme concept de base, mais trop intuitive
Les mathématiciens autour de l'École polytechnique
Lagrange
La série comme fondement du calcul.Lazare Carnot
Sylvestre François Lacroix
Le XIXe siècle - vers la rigueur
Louis Augustin Cauchy (1789-1857)
La limite comme fondement du calcul. Définition rigoureuse de limite.
La construction des réels, puis l'axiomatisation des entiers.
L'infini (Cantor)
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |