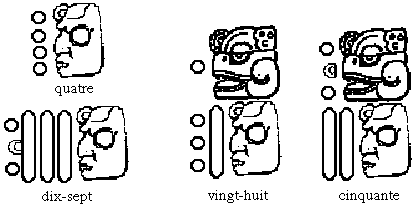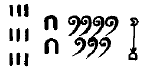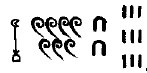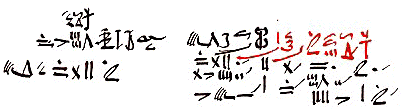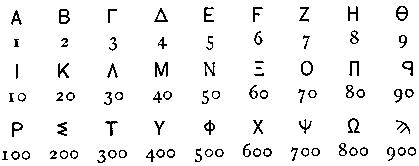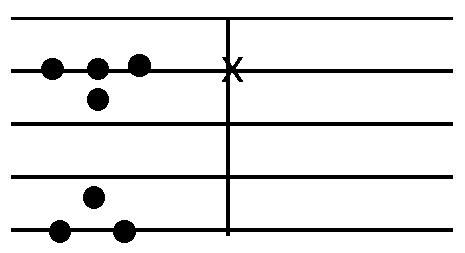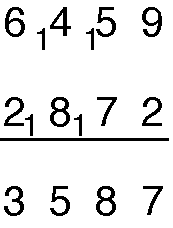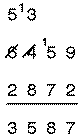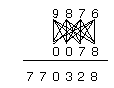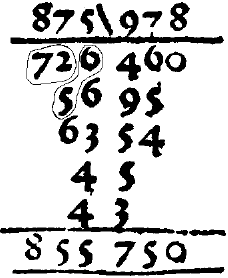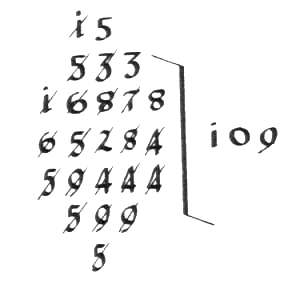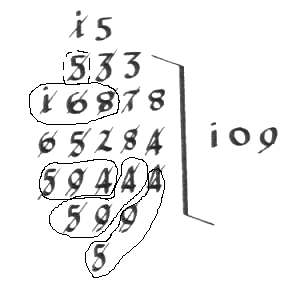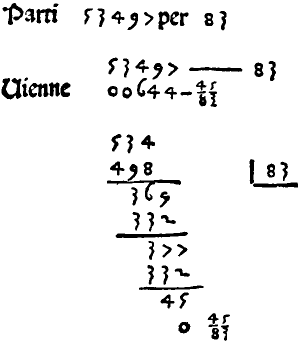MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Nombres et Fractions
L'écriture des nombres naturels
En guise d'introduction, les mots pour parler des nombres
De un à dix
De dix à vingt
Les soldats et colons romains
De vingt à cent
Les Vikings
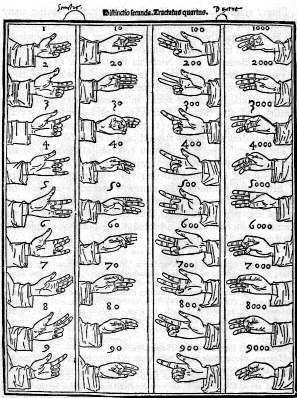
Compter avec les mains
Comput digital, Luca Pacioli, Suma de Arithmetica ... , 1494
D.E. Smith, History of Mathematics, vol. II, New York : Dover, 1958, p. 199.
Les numérations écrites
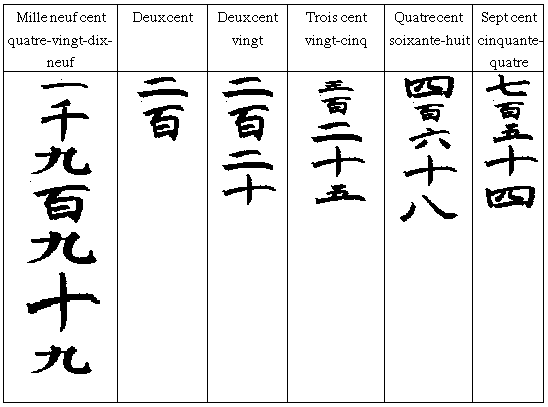
Numération chinoise (encore employé)
Trouvez la valeur de chacun des symboles dans la numération chinoise à partir des exemples suivants.
Déterminer la valeur des nombres suivants
Numération Maya (stèles et calendriers, vers 1000 de notre ère)
Déterminer la valeur des disques et des barres à l'aide des exemples suivants.
(Ne pas tenir compte des masques.)
Le Symbole symbolisant l'absence de symbole :
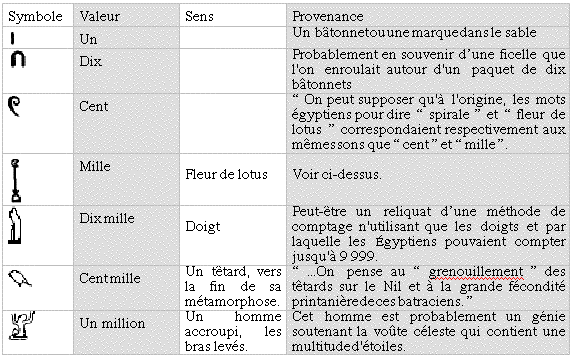
Numérations égyptiennes
-
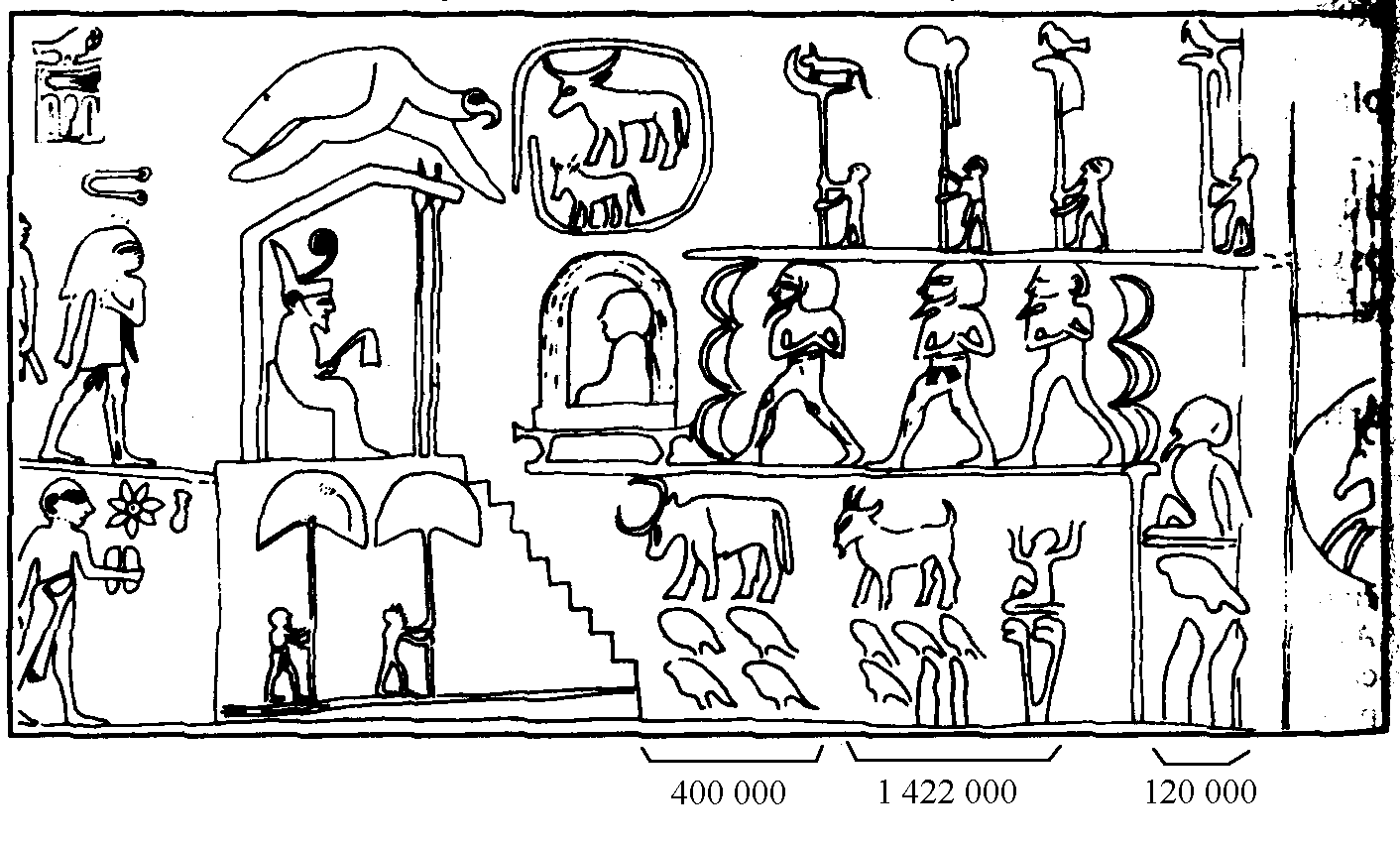
Numération hiéroglyphique (vers 3000 avant notre ère)
Déterminer la valeur des symboles numériques dans le bas à droite du dessin.
Écriture du nombre 1729 :
de droite à gauche :
de gauche à droite :
Tableau de l'origine des symboles
-
Numération hiératique

Tiré de Clawson Calvin C., The Mathematical Traveler, Exploring the Grand History of Numbers, NweYyork : Plenum Press, 1994, p. 69.
Pouvez-vous retrouver les nombres dans le problème (24) suivant du Papyrus de Rhind ?
Le problème posé est : Une quantité et son septième ensemble deviennent dix-neuf. Quelle est cette quantité ?
Numération mésopotamienne (Babylone)
Le nombre 4212 3/60
|
|
|
|
|
|
60x60
|
60
|
1
|
1/60
|
3600 + 600 + 12 + 3/60
Numération grecque (attique)
D.E. Smith, History of Mathematics, t. II, New York : Dover, 1958, p. 52.
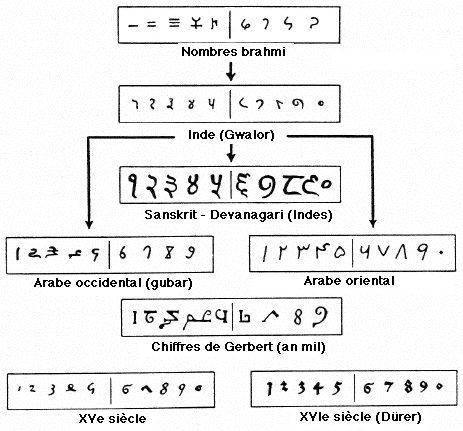
Numération indo-arabe
-
L'importance des tables de sinus dans l'histoire de la numération indienne
(B.L. van der Waerden, Science Awakening, New York : Oxford Un. Press, 1961, pp. 53-58.)
L'invention de la numération positionnelle indienne date probablement de vers 600. D'abord utilisée par les astronomes puis, après de nombreuses années, par les gens ordinaires.
Les nombres poétiques : la mémorisation des tables de sinus.
Vers 500, pour apprendre les tables de sinus, les astronomes associaient à chaque chiffre un mot qui le rappelait (ex. 1 : lune, bouche; 2: ailes, oreilles, yeux; 0: trou; etc.) de façon à transformer les tables en poèmes rimés. On rencontre cela dans le Surya-siddhanta (7e siècle) mentionné ci-dessus.
Aryabhata avait développé un système de syllabes qui exprimait à la fois les chiffres et l'ordre de grandeur de ce dernier (ex. ca voulait dire 6 unités (le a indiquant les unités ou les dizaines, le c signifiant 6), gi signifie 3 centaines (g: 3, i: centaines) etc.), ainsi cayagiyinusuchlr signifie 63335775 (du plus petit au plus grand de gauche à droite), pour nous : 57753336.
Son disciple Bhaskara simplifie en enlevant les lettres pour les ordres de grandeurs. Il utilise un zéro. C'est un système positionnel.
-
La généalogie de notre système de numération
Karl Menninger, Number Words and Number Symbols, A Cultural History of Numbers, Cambridge, Mass. : MIT Press, 1977, p. 418.
Origine des mots chiffres et zéro :
Les hindous employaient le terme sunya , le vide, pour désigner ce que nous appelons aujourd’hui le zéro. Lorsque les Arabes s’approprièrent la numération positionnelle des Indous, ils traduisirent sunya par as-sifr, qui veut aussi dire le vide. Les traducteurs européens conservèrent l’assonance sans égard au sens et écrivirent cifra ou ciphirum (comme le fait Fibonacci). Des ces mots, les français formèrent le mot chiffre. En italien, on employa zefiro, puis zefro qui devint zéro dans le dialecte vénitien, mot que les français adoptèrent aussi.
Mais il y a tout de même un problème. Les deux mots, chiffre et zéro, voudraient dire la même chose. C’est que le zéro fut un des éléments les plus troublants du nouveau système et il en devint en quelque sorte, dans l’esprit populaire, la marque identificatrice qu’on associait à tous ces signes, à l’origine bizarres, que sont les chiffres de 1 à 9.
Au XVIe siècle, le mot chiffre prend uniquement le sens qu’on lui connaît maintenant.
Calculer avec les nombres
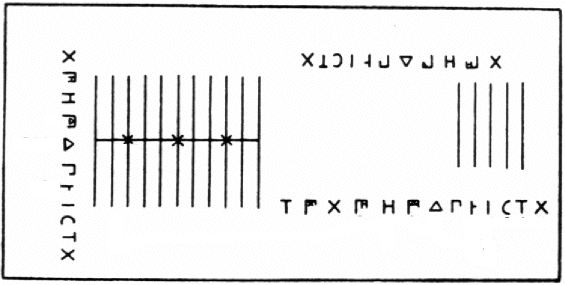
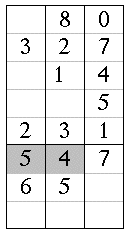
Compter sur une table à calculer
Table de Salamis
Menninger, Karl, Number Words and Number Symbols, A Cultural History of Numbers, Cambridge, Mass. : M.I.T. Press, p. 303.
3507 sur une table à calculer du XIIIe siècle
Cinq mots reliés à la table à calculer
-
Abaque
Le mot abaque vient du grec abakion, lui-même dérivé du mot abax qui signifie plateau rond ou coupe sans pied. (Menninger, p. 301.) On conçoit dès lors que les premiers abaques avaient une surface plane, pouvant être une table ou un genre de plateau. -
Calcul
On parle souvent de « calcul rénaux ». Dans cette expression, le terme calcul fait référence à une pierre au rein. C’est qu’en latin, calculus veut dire pierre. Or les pierres servaient à effectuer les opérations arithmétiques élémentaires avec les tables à calculer. Calculer, utiliser les pierres, devint donc synonyme d’effectuer les opérations élémentaires, et ce même après que les tables à calculer ne furent plus nécessaires pour effectuer ces opérations. -
Comptoirs et Bureau
Au Moyen Âge, le commerçant, ou la banquier, se tenait habituellement derrière sa table à calculer. Dans le mot comptoir, il y a le mot compte… en souvenir de cette pratique oublié. Lorsqu’on ne calculait pas ou on n’avait pas besoin de la table à calculer, on la recouvrait d’un tissus appelée une bure. Le bureau est ce comptoir recouvert d’une bure. Par la suite, les sens s’est étendu au lieu où était la table à calculer.
Jetons
Vient de ce qu’on appelait calcul à jet le calcul avec des calculi sur une table à calculer. On « jetait » les calculi sur les lignes de la table. (Smith, II, p. 192.)
Le commerce au XIVe siècle
Tiré de : Les Cahiers Science & Vie, no. 63, juin 2001, Pierre Ribémont, et Max Lejbowicz, Nicole Oresme, un mathématicien citoyen , pp. 76-80, p. 79.
Les algorithmes de calcul avec la numération indo-arabe
Addition 80 + 327 + 14 + 5 + 231
Maximus Planude (1260-v.1310) Byzance
Baha Eddin (1547-1622) Syrie
Bhaskara (Lilavati) (1114-v. 1185) Inde
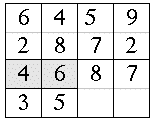
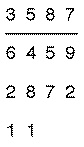
Soustraction : Soustraire 2872 à 6459
Évitement de l'emprunt
Bhaskara (Lilavati)
Au lieu de faire directement la soustraction, on considère le complément 2872 à 10000. On l’additionne au nombre dont on soustrait puis on enlève le 10000 de la somme obtenue. Schématiquement :
10000 –2872 -> (2 à 10 : 8, 7 à 9 :2, 8 à 9 :1, 2 à 9 :7) -> 7128
6459 + 7128 -> 13587
13587 – 10000 -> 3587 (qui est le nombre cherché) [On pourrait dire aussi enlever le 1 à la somme trouvée l’étape 2]
Que se passe-t-il lorsque le nombre dont on soustrait a plus de chiffres que celui qui est à soustraire ?
Cet algorithme est-il effectivement plus simple que le nôtre ?
Pourquoi cet algorithme fonctionne-t-il ?Ramus (Pierre de la Ramée, 1515-1572)
Une dernière méthode, qui s’effectue de gauche à droite, consiste à littéralement éviter l’emprunt.
En voici les étapes, en rayant les chiffres à mesure qu’on les a utilisés.
1) 6 – 2 -> 4.
2) 4 – 8 étant impossible, faire 44 – 8 -> 36.
3) 5 – 7 étant impossible, faire 65 – 7 ->58.
4) 9 – 2 -> 7.
Cette méthode exige une bonne capacité à soustraire mentalement un nombre à deux chiffre d’un nombre à un chiffre.Emprunt et retenue
Baha Eddin
Fibonacci (Léonard de Pise, Léonard Bigollo 1170 - v. 1241)
Planude
Joannes Buteo (v. 1525) Italie
Abraham ben Ezra (v. 1140)
Multiplication
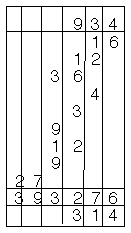
Exhiber toutes les multiplications intermédiaires (Luca Pacioli, 1445-1510)
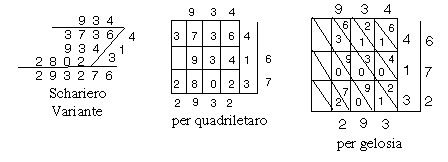
Disposition efficace des multiplications partielles
(Italie, XVe - XVIe siècles et Gerbert d'Aurillac (938-1003)934 multiplié par 314
Disposition élégante
Per copa : le premier exemple de multiplication imrpimé en Amérique (Mexique) en 1556.
978 multiplié par 875
Du Sumario Copedioso de Juan Diez, Mexico, 1556
D.E. Smith, History of Mathematics, t. II, New York : Dover, 1958, p. 119.
Algorithme sans référence aux tables de multiplication - la duplication
Égypte
Multiplier 81 par 57, c’est dire répéter 81, 57 fois.
Je prends 81, une fois.
Je double 81, ce qui fait 2 fois 81 -> 162.
Je double 162, ce qui fait 4 fois 81 -> 324.
Je double 324, ce qui fait 8 fois 81 -> 648
Je double 324, ce qui fait 16 fois 81 -> 1296.
Je double 648, ce qui fait 32 fois 81 -> 2592.
Il est inutile de doubler encore, puisque alors j’aurais 64 fois 81, alors que je ne veux répéter 81 que 57 fois.
Maintenant, je cherche la combinaison de duplications successives de deux (on pourrait dire des puissances de 2) qui, additionnées ensemble, donnent 57, le multiplicateur. En tâtonnant, je trouve 32, 16, 8 et 1. Le produit de 81 par 57 est donc 2592 + 1296 + 648 + 81, c’est-à-dire 4617.
Les Égyptiens écrivaient (traduit dans notre écriture) cela ainsi
La méthode russe
Il existe une méthode d’où le tâtonnement est éliminé. Il s’agit de la méthode russe, employé au jusqu’au début de XXe siècle en Russie. Reprenant une forme qui rappelle celle des Égyptiens, on écrit plutôt
Où, dans la première colonne de chiffres, on a 57 divisé successivement par 2, sans tenir compte du reste. On marque à gauche les lignes dans lesquelles les nombres de cette colonne sont impairs et l’on additionne les multiples de 81 qui sont en regard. Cette dernière somme nous donne le produit cherché. Oh là ! Mais pourquoi cela marche-t-il ?
Regula pigri (la règle des paresseux - table de 5 x 10)
Mais il y une façon de réduire notre connaissance des tables à une table de 5x10. C’est ce qu’ont proposé, sous le nom de regula pigri, la règle des paresseux, de nombreux calculateurs des XVe et XVIe siècles. La voici sous sa forme utilisant les mains. Pour multiplier deux nombres compris entre cinq et dix, associant un nombre à une des deux mains, et l’autre à l’autre, levez le nombre de doigts qu’il faut ajouter à cinq pour avoir chaque nombre. Pour connaître le produit des deux nombres, il suffit de prendre le nombre de doigts levés, ce qui donne le nombre de dizaines et d’ajouter le produit des doigts repliés. Ainsi, 9x9. Quatre doigts levés dans chaque main. Il y a donc huit dizaines (80) auxquelles j’ajoute le produit de un par un, c’est-à-dire un. Le produit de 9 par 9 est donc 81.
Pourquoi cela marche-t-il ?
Division
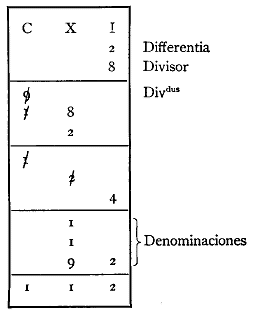
Gerbert d'Aurillac
La méthode de Gerbert se réfère, comme toujours chez lui, à son abaque.
Voici la division de 900 par 8.
On a clairement besoin de donner des explications. Chacune des colonnes correspond aux ordres de grandeurs indiquées au haut de la colonne. Remarquez l’usage des nombres latins pour préciser l’ordre de grandeur. Le dividende (dividandus) est 900, alors que le diviseur est 8. ? Afin d’éviter des questions du style « combien de fois 8 va-t-il dans 900 ? », Gerbert va diviser par 10-2, d’où le 2 appelé Differentia. On peut suivre la suite de ses actions.
Combien de fois 10 va-t-il dans 900 ? 90 fois. Dix fois 90 donne 900. Je raie le 9 de la colonne des centaines. J’écris 9 en bas dans la colonne des dizaines. Mais puisque je divise par 10-2, il y a en réalité encore 90x2, 180, qu’il faut diviser par 8.
Combien de fois 10 va-t-il dans 180 ? 10 fois (Remarquer qu’il ne prend pas la plus grande valeur possible, mais la valeur la plus immédiatement visible). J’écris 1 en bas dans la colonne des dizaines. Je raie le 1 du 180 et j’ajoute 20 pour combler l’effet du –2 dans 10-2. La somme de 80 et 20 donne 100. Je place 1 dans la colonne des centaines.
Combien de fois 10 va-t-il dans 100 ? 10 fois. Je raie le 1 dans la colonne des centaines. J’écris 1 en bas dans la colonne des dizaines. Il me reste à tenir compte du 20 pour combler l’effet du –2. J’écris donc 2 dans la colonne des dizaines.
Combien de fois 10 va-t-il dans 20 ? Deux fois. Je raie le 2 dans la colonne des dizaines et j’écris deux en bas dans la colonne des unités. Il me reste 4, 2x2, dont je n’ai pas tenu compte.
Je fais la somme des nombres en bas, c’est-à-dire 90, 10, 10 et 2. J’écris la somme tout en bas, 112. La réponse est 112, reste 4.
Économiser de l'espace : Per Galeo (Italie, XVe - XVIe siècles)
Il s’agit de la division de 65284 par 594, dont la réponse est 109, reste 538. Voici une illustration qui vous aidera. Remarquez que 1 fois 594 donne 594 et que 652 – 594 donne 58.
Une jolie division per Galeo (vers 1575)
965347655446 divisé par 6543218, ce qui donne 147534 avec un reste.
Les deux exemples sont tirés de Swetz, Capitalism & Arithmetic, The New Math of the 15th Century, La Salle, Ill. : Open Court, 1987, p. 215.
Première division imprimée (1491)
Calandri, 1491
Swetz, Capitalism & Arithmetic, The New Math of the 15th Century, La Salle, Ill. : Open Court, 1987, p. 220
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |