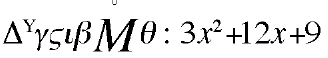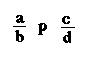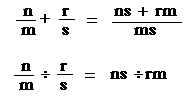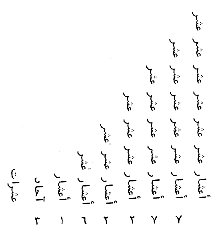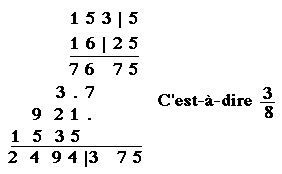MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Les fractions (1)
Les fractions
Problématiques de l'histoire des fractions
Les fractions
Problématiques de l'histoire des fractions
- Pour nous, il y a trois sens à l'expression a/b : division, rapport, fraction
- Rapport : une comparaison
- Fraction : Mesure
- Rapport de mesures
- Fractions communes (tant de parties dans un tout divisé en un certain nombre de parties égales)
- Fractions décimales
- Il faut aussi s'intéresser à deux aspects de
chacun des ces aspects :
- Le symbolisme, et les manipulations opératoires qui y sont appliquées
- Les appellations utilisées
L'Antiquité
L'Antiquité
-
Dans les mathématiques nobles - Grèce
Pythagore
- le rapport numérique permet de découvrir
les relations cachées dans la nature.
Musique, médecine, etc.
- La découverte des incommensurables : besoin de rapport entre grandeurs incommensurables. Rôle central de la géométrie.
Platon : le calcul noble, rôle de la monade.
- L'arithmétique est divisée en deux parties
:
- L'arithmétique pratique, issue de mesures d'objets réels (les objets sont indéfiniment divisibles)
- L'arithmétique théorique, basée sur la notion de monade, indivisible, le Un absolu.
- La fraction (rapport numérique ou rapport de grandeurs) n'est pas un nombre. Le Un n'est d'ailleurs pas non plus un nombre.
- Difficultés des relations entre nos trois
sens de fractions :
- Les rapports se traitent dans le cadre de la géométrie (Euclide, Éléments, Livre V), sans référence à quelque mesure que ce soit. Non numérique.
- Les fractions : comparaison de deux nombres, donc en arithmétique. Dans l'arithmétique, vue plutôt comme un changement d'unité de mesure.
- La division : application des aires, si en géométrie (changement de dimension), sens arithmétique, si en arithmétique.
- le rapport numérique permet de découvrir
les relations cachées dans la nature.
-
Les mathématiques de bas étage
Égypte (Papyrus de Rhind, par le scribe Ahmes, vers -1550 av. notre ère)
- Fractions unitaires
- Notation
Équation équivalente à x(2/3 + 1/2 + 1/7 + 1) = 37.

(Smith, D.E., History of Mathematics, tome 2, p. 422.)
Les trois premiers hiéroglyphes signifient « masse » (prononcé ahe ou hau) et tient lieu d'inconnue.
- Exemple d'un développement plus
complexe :
2/43 = 1/42 + 1/86 + 1/129 + 1/301.
La fraction 2/43, semble à la fois un rapport et une division (2 divisé en 43 parties).
- Importance des rapports : la règle de fausse position
Problème 24 : Une quantité et son septième ajoutés ensemble deviennent dix-neuf. Quel est cette quantité ?
Supposons 7
\17\1/71
total8Autant de fois 8 doit être multiplié pour donner 19, autant de fois 7 doit être multiplié pour donner le nombre requis.
18\216
1/24\1/42\1/81Total2 1/4 1/8
\12 1/4 1/8\24 1/2 1/4\49 1/2Fait cela donc :
La quantité est16 1/2 1/81/72 1/4 1/8Total19- Exercice : Résoudre Une quantité et son cinquième ajoutés ensemble deviennent vingt-et-un. Quel est cette quantité ?
- Exercice : Que devait faire le scribe pour
mettre au carré le nombre fractionnaire 61 1/3 1/9 ?
(voir Smith, t. 2, p. 224)
Mésopotamie
- Extension du système positionnel sexagésimal
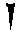
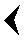
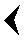
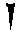
 60x606011/60
60x606011/60Exemple d'écriture
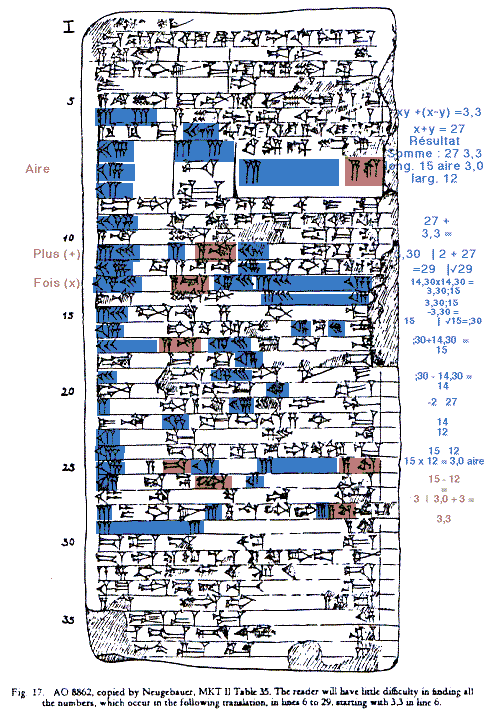
(Tiré de van der Waerden, Science Awakening)
- L'opération de division s'opère à l'aide d'une table d'inverses.
Voici le début d'une telle table. N.B. Il manque des inverses (pourquoi ?) :
1:230
1:87;301:320
1:96;401:415
1:1061:512
1:1251:610
1:154(tiré de Van der Waerden, Science Awakening, p. 43)
Un exemple de problème où par ailleurs la table est inutile, mais où on voit clairement la manipulation des fractions
J'ai additionné sept fois le côté de mon carré et onze fois la surface : 6°15'. Tu inscriras 7 et 11. Tu porteras 11 à 6°15' : 1`8°45'. Tu fractionneras en deux 7 : 3°30'. t croiseras 3°30' et 3°30' : 12°15'. Tu ajouteras à 1`8°45' : 1`21°. C'est le carré de 9. Tu soustrairas 3°30', que tu as croisé, de 9 : tu inscriras 5°30. L'inverse de 11 ne peut être dénoué. Que dois-je poser à 11 qui me donne 5°30' ? 30', son quotient. Le côté du carré est 30'.
(Tiréde Dedron, Itard, Mathématique et Mathématiciens)
- Fractions unitaires
La Grèce hellénique (Smith, D.E., History of Mathematics, t. 2)
Habituellement, écriture sou forme de fraction unitaire : une ou des lettres grecques représentant un nombre accompagnée(s) d'un symbole (parfois un ") indiquant qu'il s'agit d'une fraction.
1/4:
Quelques fractions ont des symboles particuliers, par exemple, 1/2,
, 2/3,
, qui signifie 1/2 + 1/6.
Chez Aristarque (v. 260 av. notre ère)
10 soixante et onzième :
.
Ou encore 2/5 :
La Grèce hellénistique
Héron d'Alexandrie (v. 50) et Diophante (v. 275)
On retrouve la forme actuelle, mais sans barre et inversée. 19/4 s'écrit 19 au-dessous de 4.
Diophante (v. 275), dans son Arithmétique
Il développe aussi une notation pour ce que nous écrivons 1/x, 1/x2 :
. Remarquons l'usage de la monade, spécifiquement représentée. Les fractions sont tout de même manipulées comme des nombres.
Dans la vie de tous les jours
La notation des fractions dans la vie de tous les jours est toutefois évitées par l'usage des unités de poids, qui servait aussi pour la monnaie. Ainsi,à Alexandrie au début de notre ère, on avait la table de correspondance suivante, à partir de la plus petite unité de mesure, le chalque :
Chalque
Huit chalques est une obole
Six oboles est une drachme
Cent drachmes est un mna
Soixante mnas est un talent
:Il faut retenir le facteur de passage d’une unité à l’autre, car elles sont chaque fois différentes Les calculs s’en trouveront d’autant complexifiés. Cela nous rappelle le système anglais avec ses pieds, ses verges, ses milles. Par ailleurs chaque unité a un symbole :
Un chalque : X, une obole : I, une drachme :
, un mna : H, un talent : T.
Il est aussi possible d’écrire des parties d’oboles. Ainsi la demi-obole se note C, le quart d’obole est représenté par T (à ne pas confondre avec le talent, même si le symbole est identique) et le huitième, le chalque, par X. Pour écrire une fraction de drachme, on se ramène à l’obole et à ses subdivisions. Ainsi, pour la huitième partie de drachme, on écrira C X X. Pour la quatrième partie, on écrira I C. Les enfants avaient ainsi à apprendre des tables de « fractions ».
On voit ces symboles sur la table à calculer de Salamis.
Les fractions unitaires restent les fractions utilisées dans la vie de tout les jours, si des fractions doivent effectivement être utilisées. Ainsi, une expressions comme « quinze seizième » sera écrite comme 1/2 + 1/4 + 1/8 + 1/16. (Smith, D.E., t. 2, p. 214)
Rome
À Rome, l'élève doit apprendre un autre système de fractions, basé sur douze, le toute avec un vocabulaire complexe :
Calcus
Huit calcus est un scrupule
Vingt-quatre scrupules est une once
Douze onces est un as (monnaie) ou livre (poids)On voit, avec ce second exemple, que les systèmes de mesure dont le facteur de conversion varie d’un niveau de passage à l’autre sont la règle. La belle régularité de notre système international constitue en fait une exception.
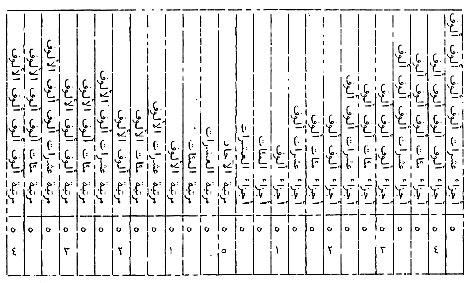
À Rome, le vocabulaire de l’once sert souvent pour nommer les parties d’un tout. Mais ce vocabulaire se révèle complexe. Pour parler des différents nombres d’onces, le Romains ne disent pas simplement, « une once, deux onces, trois onces, …, dix onces, onze onces », mais ils utilisent un vocabulaire complexe comme le montre le tableau qui suit. Dans les calculs, on se limite aux scrupules et l’on néglige les calcus.
as deunx Moins une once (de uncia) Dextans
ou
Decunx
ou
Semis et triens
Moins un sixième (d'as)
(de sextans)dix onces (decem uniciae)
Une demie et un tiers d'as
Dodrans Moins un quart (d'as)
(de quadrans)Bes Deux parties d'as
(bis triens)Septunx sept onces
(septem unciae)Semis Demi-as
(Semi-as)Quincunx Cinq onces
(quinquae unciae)Triens Le tiers (d'as) Quadrans Le quart (d'as) Sextans Le sixième (d'as)
Uncia Once
Par ailleurs ce lourd vocabulaire transforme les calculs même simples en un difficile exercice de mémoire. Voici un exemple de la façon dont on récite les calculs sur les fractions : « Réponds, fils d’Albinus ; si d’un quincunx (cinq onces) tu enlèves une once, que reste-t-il ? Allons, qu’est-ce que tu attends pour répondre ? — Un triens. — Bien : tu sauras défendre tes sous ! Si (au contraire) on y ajoute une once, qu’est-ce que çà fait ? — Un semis (une moitié). » Pas surprenant que certaines écoles romaines aient eu un spécialiste, le calculator, qui enseignait ces manipulations à quelques élèves qui se destinaient au commerce ou à devenir fonctionnaires. D’ailleurs on peut ici remarquer que l’usage d’un vocabulaire étriqué pour les fractions a certainement limité la compréhension des pauvres élèves, et, sans doute, des maîtres.
Un dernier exemple :
seize as égale un denarius
un as : denarii semuncia sicilicus (1/24 + 1/48 de denarius)
trois as : denarrii sextans sicilicus (1/6 + 1/48 de denarius).
En Inde
Origine de notre notation (la position et la barre, même si elle n'était pas toujours là dans les faits)
Brhamagupta (v. 628) et Bhaskara (v. 1150)
Le monde Arabe
Les fractions « ordinaires »
Définition de fraction
En général, une fraction est « une quantité considérée dans son rapport à un tout pris comme unité. » (al-Kasi?)
Les traditions reliées aux fractions
- Le calcul indien, utilisant la planche à poussière.
- Le calcul sexagésimal, pour les astronomes.
- Le calcul digital, avec les mains et les doigts, dit le calcul arabe.
- Le calcul byzantin, dit le calcul romain.
Nomenclature des fractions
En ce qui concerne la façon de nommer les fractions, il y a deux grands types de fractions.
- Les fractions ouvertes (ou simples) (1/n, 2 < n < 10), qui ont un mot propre.
1/3 : tult ; 2/3 : deux tulta (On n'utilisait pas de symboles, seulement des mots)
1/5 : hums ; 3/5 : trois humsa
L'usage de ce vocabulaire rendait au départ la manipulation des fractions difficile. C'est pourquoi la méthode digitale était importante. De même pour la méthode indienne, qui elle utilise un symbolisme.
- Les fractions non ouverte (ou sourdes) (1/n, n >10) qui sont simplement décrites par une expression comme « trois de treize parties » pour 3/13.
De ces catégories primaires, Abu-l-Wafa (940-998) ajoute une autre classification:
- Les fractions exprimables : combinaison de sommes et de produits de fractions ouvertes. N.B. On voit ici encore l'importance des fractions unitaires.
- Les fractions inexprimables : les autres comme les fractions de la forme 1/p où p est un nombre premier supérieur à 10.
Dans le commerce, on rencontre parfois des transformations comme la suivante :
49/60 = 45/60 + 4/60 + = 30/60 + 15/60 + 4/60 = 1/2 + 1/4 +(2/3)x(1/10)
Symbolisme (calcul indien)
Numérateur au-dessus du dénominateur, sans trait. Mais alors possibilité de confusion.
Un exemple : 3 sens possibles:
• 25 + 2/3 + 1/7
• (5 + 2/3) + (2 + 1/7) • (5 + 2/3) x (2 + 1/7) Le trait horizontal entre le numérateur et le dénominateur apparaît dans l'ouest du monde arabe, au Maghreb, chez al-Hassar (XIIe siècle). Il sera conservé par la suite.
Un certain symbolisme, avec trait, se développe pourtant, particulièrement au Maghreb, mais il reste des ambiguïtés.
Deux interprétations • a/b(p + (c/d)) • (a/b)p + c/d
Opérations sur les fractions
Sept opérations (en Orient) sur les entiers étendues aux fractions : addition, soustraction, duplication, dimidiation, multiplication, division , racine nième.
Puis les opérations spécifiques sur les fractions : conversion (transformer une fraction en une autre ayant un dénominateur donné, utile pour les opérations commerciales), simplification, comparaison, réduction au même dénominateur.
La présentation de ces opérations se fait dans de multiples sections, sans utiliser la réduction au même dénominateur pour simplifier les choses. Notez que la somme d'un entier et d'une fraction est considérée comme différente de la somme d'une fraction et d'une fraction. D'où le besoin de plusieurs sections différentes.
Dans les livres, principalement au Maghreb, on commence le plus souvent l'étude des opérations des fractions par la multiplication. Cette tradition a été introduite par al-Khwarizmi.
Les règles pour les opérations d'addition et de division sont les suivantes:
Remarquons que l'addition ne demande pas d'avoir le plus petit commun multiple, mais simplement le dénominateur commun le plus naturel, celui issu du produit des dénominateurs des fractions additionnées.La division correspond à mettre les deux fractions sur ce même dénominateur commun et, alors, à diviser les numérateurs.
La règle de division comme le produit de l'inverse du diviseur apparaît aussi au Maghreb, chez MunCim (XIIIe siècle ??) Voici la démonstation qu'il donne de cette règle :
Soit e = a/b, et r = g/d, on a e/r = e(bd)/r(db). Mais eb = a et rd = g, donc e/r = ad/bg.
Les fractions décimales
(Informations et illustrations tirées de R. Rashed, Entre artithmétique et algèbre, Recherches sur l'histoire des mathématiques arabes, Paris : Belles-Lettres, 1984, pp.122-139, 143, 144 et 127.)
Usage local de fractions où 10 jouent un rôle important, mais où les décimaux sont comme un artifice de calcul.
La règle des zéros : (a)1/n = (ax10nk)1/n/10k, pour k = 1, 2, …
Mais on transforme les réponses en fractions sexagésimales, ou en une forme non décimale.
Example :
- al-Uqlidisi (952) : pour dire une réponse trouvée en décimale 0,59375, dira 59 375 de cent mille. « Son rapport est dit un demi plus un demi huitième plus un quart de huitième. »
- as-Samawal transforme, avant son traité de 1172, la racine carré de 1020 (31,937) en 31 + 1/2 + 2/5 + 1/5 x 1/10 + 1/10 x 1/10 + 1/2 x 1/10 x 1/10 + 1/5 x 1/10 x 1/10)
Le courant arithmético-algébrique : Al-Karagi (953-1029) et as-Samaw'al (v. 1130-1180)
Invention des fractions décimales
- Al-Karagi : développement d'une arithmétique de l'inconnue
- As-Samawal, un disciple d'al-Karagi, dans son traité Traité d'arithmétique (1172), consacré à l'extraction des racines et la résolution par approximation des équations algébriques.
Dans le cadre de l'étude des ces techniques d'approximation, naîtront les fractions décimales.
Voyons d'abord comment les polynômes étaient représentés.
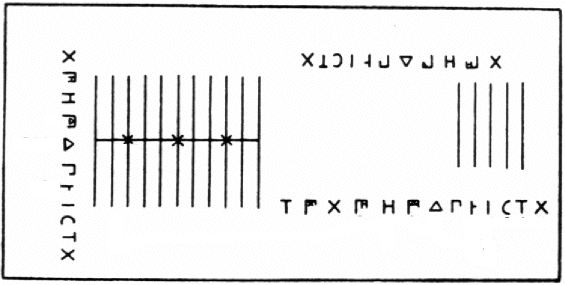
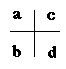
Considérons le tableau suivant :
En écrivant le coefficient des puissances de l'inconnue dans les colonnes correspondantes, on peut écrire une expression comme 3x2 + 5 + 1/x, ainsi :
Dans ce contexte, la règle des exposants, correspondant à xnxm = xn+m, s'énonce ainsi :
« Si les deux puissances sont de part et d'autre de l'unité, à partir de l'une d'elles nous comptons en direction de l'unité, le nombre des éléments du tableau qui séparent l'autre puissance de l'unité, et le nombre est du côté de l'unité. Si les deux puissances sont du même côté de l'unité, nous comptons en direction opposée à l'unité. »
La dernière section du traité est consacrée à cette nouvelle forme de calcul. Elle est intitulée :
« Au sujet de la position d'un principe unique par lequel on peut déterminer toutes les opérations de la partition (al-Tafriq) qui sont la division, l'extraction de la racine carrée, l'extraction d'un côté par toutes les puissances, et la correction de toutes les fractions qui apparaissent dans ces opérations, indéfiniment. »En identifiant les unités la puissance zéro de l'inconnue, as-Samawal peut énoncer cette règle et même l'étendre au cas où x n'est pas une inconnue mais une valeur numérique… comme 10. Par le transfert des règles comme celle-ci des polynômes aux tableaux à base 10, il obtient un système permettant de calculer avec les décimaux.
0 : parties des unités
1 (à droite) : parties des dizaines
1 (à gauche) : parties des dizaines (en fait les dixièmes)Voici la racine carré de 10 :
Pour prononcer les fractions, il les ramène à une fraction sur le dénominateur de la plus petite fractions décimale. Ainsi, la racine carré de 10 se lit 3 unités plus 162277 parties de 1 000 000 parties. (À la façon habituelle de nommer les fractions chez les Arabes). Dans la notation, il sépare la partie décimale de la partie entière par un signe, comme une barre verticale.
On voit donc que les fractions décimales viennent de la pratique des opérations sur les polynômes exprimés sous forme de tableaux.
Après as-Samawal, vers al-Kashi (1436-7)
Il est difficile de savoir quel a été l'influence des fractions décimales d'as-Samawal. On sait toutefois qu'elles étaient utilisée par les comptables des administrations de Tunis, probablement au XIVe siècle ou au début du XVe siècle.. C'est toutefois un exemple documenté unique. En était-il de même dans d'autres administration ? D'ailleurs, il n'est pas certain que l'usage des fractions décimales aient été fait avec les même outils que ceux d'as-Samawal et al-Kashi. (Djebbar, A., Le traitement des fractions dans la tradition mathématique médiévale du Maghreb, Prébublications, Université de Paris-Sud, Mathématiques, 90-04, p. 28-29)
Toutefois, dans le livre Clé d'Arithmétique (1436-7) d'al-Kashi , les fractions décimales sont non seulement abordées, elles sont aussi nommées (al-Kusur al a'shariyya), ce que n'avait pas fait explicitement as-Samawal. Al-Kashi se sert aussi des fractions décimales dans sont Traité sur la circonférence du cercle pour approximer Pi, à 16 décimales près. Au-delà du noms données à ces fractions, deux nouveautés, par rapport à as-Samawal, marque le travail d'al-Kashi :
- Une analogie explicite et détaillée est faite avec les fractions sexagésimales
- Les fractions décimales ne servent plus simplement à approximer les racines, mais aussi les nombres réels, comme Pi.
Le transfert vers l'Occident
On a peu d'infomations précises sur le transfert de ces connaissances des fractions décimales vers l'Occident chrétien. Un manuscrit byzantin apportéà vienne en 1562, indique tout de même que les Turcs employaient les fractions décimales pour la multiplication et la division. Selon ce manuscrit, les calcul se faisaient ainsi:
Énoncé du problème : Calculer le prix de 153 1/2 mesures de sel, le prix de chacune étant de 16 1/4 aspra. C'est-à-dire 153 1/2 • 16 1/4.
Voici le calcul :
Dans cet exemple, les lettres grecques ont été remplacée (par moi) par nos chiffres. Remarquons la barre, qui sépare la partie entière de la partie fractionnaire, et le point, pour le zéro. La fraction décimale est aussi réécrite en fraction ordinaire.
L'usage des fraction décimales en Europe précède l'époque de ce manuscrit. (Rudolff, Cardan par exemple. Voir la prochaine leçon)
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |