|
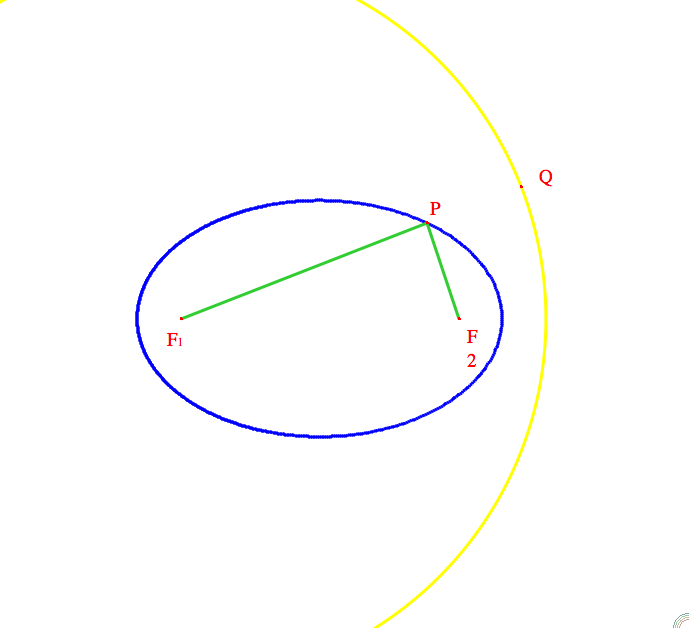
Les lieux géométriques : ellipses et hyperbolesOn peut définir une ellipse en tant que lieu géométrique comme suit. Dans un plan donné, nous avons besoin de deux points F1 et F2 (qui seront appelés les foyers de l'effipse) et aussi d'un nombre c qui est supérieur à la distance entre les deux foyers. L'ellipse sera la courbe formée par l'ensemble de tous les points P du plan vérifiant la propriété suivante:distance(P,F1)
+ distance(P,F2) = c.
Cette
situation est représentée dynamiquement par la
figure Cabri
ci-dessous,
où les deux distances aux foyers sont
représentées par des segments et
où le nombre c
correspond au rayon du cercle pâle (dont on ne voit
initialement qu'un
arc).Via la souris, on peut déplacer les foyers et modifier le rayon du cercle. Par contre, on ne peut déplacer directement le point P sur la conique: il faut agir par l'intermédiaire du point Q sur le cercle pâle. On constate alors que le point P se trouve toujours à l'intersection de la conique et de la demi-droite issue de F1 et passant par Q. Que ce soit en
déplaçant le foyer F2
ou en changeant le rayon du cercle pâle, si le second
foyer
vient à
sortir du cercle pâle, l'ellipse semble se transformer en
hyperbole : on
peut en effet vérifier que | distance(P,F1)
- distance(P,F2) |
= c
puisque, par construction de
la figure Cabri,
on a toujours distance(P,Q) =
distance(P,F2).
Appendice technologiqueLa figure Cabri ci-dessus est, en fait, une image : un clic sur celle-ci permet de télécharger ladite figure. |