|
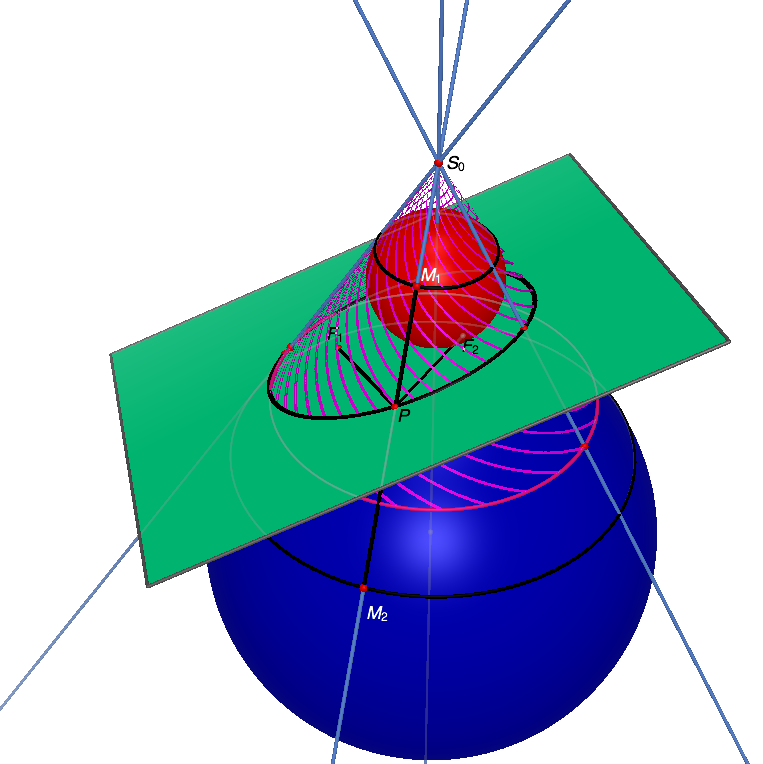
Passage des sections coniques aux lieux géométriquesÉtant donné une section de cône, comment passer au lieu géométrique correspondant ? Dans le cas de l'ellipse, par exemple, ceci nécessite tout d'abord de trouver les foyers F1 et F2 ainsi que la constante c, pour ensuite vérifier la propriété caractéristique d'une ellipse en tant que lieu géométrique : un point P est sur la courbe si et seulement distance(P,F1) + distance(P,F2) = c.Le mathématicien français Pierre Dandelin nous a légué une élégante approche géométrique pour résoudre ce problème. Elle repose sur l'utilisation de deux sphères, dites sphères de Dandelin, qui sont tangentes à la fois au cône et au plan secant (voir la figure Cabri 3D ci-dessous). Les foyers cherchés seront en fait les points de contacts des deux sphères avec le plan tangent, tandis que la constante c sera égale à la distante entre les deux cercles de tangence entre les sphères et le cône. Comment manipuler les éléments de la figure ?
Appendice technologiqueLa figure Cabri 3D ci-dessus est, en fait, une image : un clic sur celle-ci permet de télécharger ladite figure. |