Leonardo Bigollo, Leonard de Pise ou plus communément appelé Fibonacci fut un grand mathématicien du Moyen-Âge. Il est né à Pise en Italie vers 1170 et est mort, vers 1250.

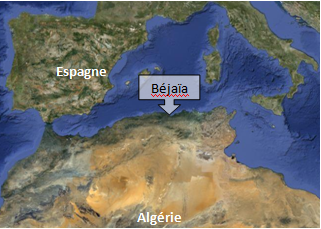
    Guilielmo Bonaccio, son père, était consul à Béjaïa, connue aussi sous son nom francisé : Bougie. Au Moyen-Âge, Bougie est une cité très prospère de la côte méditerranéenne. Elle est située sur les côtes de Kabylie en Algérie. Leonardo suivit donc son père en Algérie où il apprit l’arabe et découvrit les chiffres indo-arabes.

    Il apprécia grandement ces derniers et se fit propagandiste des avantages à les préférer aux chiffres romains. Il écrit à ces propos dans un de ses livres les plus connus, Liber abaci, le livre de l’abaque (boulier). Ce livre introduit les chiffres indo-arabes en Europe. En effet, on y découvre le zéro, le système positionnel et les critères de divisibilité par 2, par 3,… .

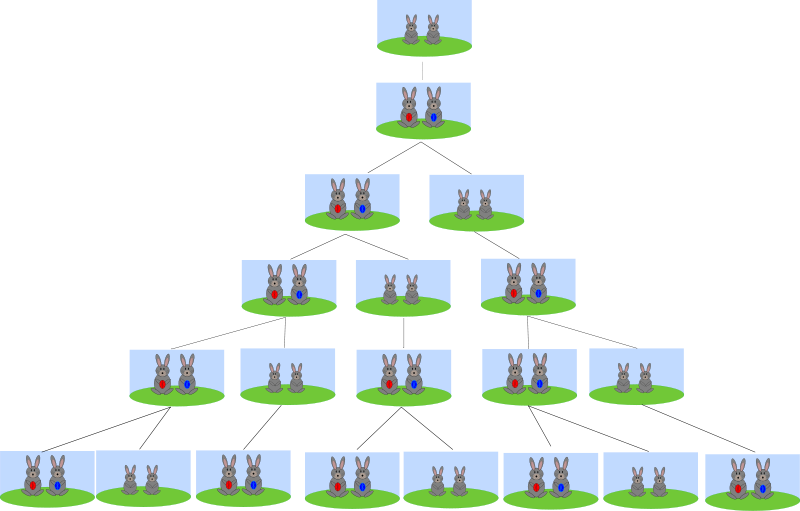
    Fibonacci fut celui qui inventa la notion mathématique de suite de nombres. Dans la troisième partie de son livre, Liber abaci, il pose un problème: « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du deuxième mois de son existence? ». La série obtenue est la suite de Fibonacci :

            1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…

    En effet, si on commence avec un couple de lapins au mois de janvier, au mois de février, ils sont prêts à engendrer. Au mois de mars, on a donc un nouveau couple de lapins plus le couple que nous avions au départ, on a deux couples. Au mois d’avril, le premier couple met au monde un nouveau couple. On obtient donc 3 couples de lapins. Et ainsi de suite.

 

    En seulement une année, un couple de lapins met au monde 233 couples de lapins! Si l’on porte attention à la suite, on s’aperçoit qu’on obtient les nombres qui suivent en additionnant les deux nombres précédents (1+1=2, 1+2=3…). Cette suite apparait dans beaucoup d’éléments des mathématiques et des sciences.

     Cette suite est la plus célèbre de Fibonacci. Elle est même utilisée dans le livre de Dan Brown, Da Vinci Code.