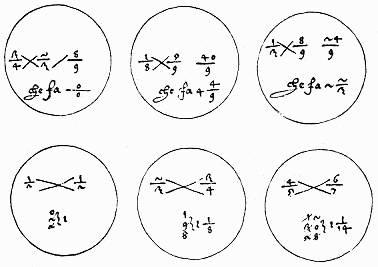MAT 6221

Bas de la page

Les fractions (2)

Les fractions en Europe

Les fractions ordinaires

Le symbolisme

Nous avons vu que les Arabes du Maghreb avaient introduit la notation de fraction avec le numérateur au-dessus du numérateur, avec une barre entre les deux. Cette pratique se répandra aussi en Europe au Moyen Âge. Lorsqu'apparaît l'imprimerie (1446, premier livre imprimé) la barre est parfois omise, à cause des difficultés techniques reliées à l'impression. Ce sont les même raisons qui ont pousser les auteurs à utiliser la notation avec la barre oblique (ex. 2/3). La barre horizontale est parfois utilisée avec des nombres romains.

(Smith, D.E., Hist. of Mathematics, t. 2, p. 217. Köbel, Rechen biechlin, 1514, ici éd. de 1518)

Remarquez la notation pour les centaines.

Dénomination

Le mot fraction réfère à l'idée de briser, fractionner. Cette idée remonte aux Égyptiens. En Europe, on a utilisé ce terme, en latin, dès le XII^e siècle. Auparavant, on rencontre le terme Minutiis ou Minuciae, minutes. Les deux termes seront employés indifféremment pendant le Moyen Âge. D'autres expressions sont aussi utilisées : nombres routz (Chuquet, 1484) par exemple, ou nombre rompu.

Séquence pour l'enseignement des opérations sur les fractions

Au Moyen Âge et à la Renaissance, souvent on suit l'ordre suivant : Numération (des fractions), multiplication, division, réduction, addition , soustraction.

Opérations sur les fractions

• Addition : Comme chez les Arabes, mettre sur un dénominateur commun qui est le produit des dénominateurs des deux fractions. Ce ne fut qu'au XVII^e siècle que l'usage de réduire au plus petit commun dénominateur s'est répandu.

  Voici un exemple (Smith, D.E., p. 224) : calculer 5/6 + 3/8 :
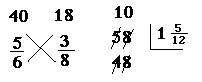
  (en fait 1 5/24). Cet exemple est tiré de l'édition de 1494 de la Summa de arithmetica, geometrica, proportioni e proportionalita de Pacioli (1445-1517)
  Exercice : Pouvez-vous interpréter l'exemple de Pacioli ?

• Multiplication : Notre méthode (multiplier les numérateurs et les dénominateurs) a été utilisée depuis les Arabes.
  Il y a eu des discussions sur le fait que, contrairement à la multiplication par un nombre, la multiplication par une fraction (inférieure à un) a un résultat inférieur au multiplicande. Par ailleurs, il y a peu de tentatives d'explication de la validité du processus de multiplication.

  Il est intéressant de noter l'influence des Grecs sur la perception qu'on avait en Europe de la façon de faire une division. Ainsi, au lieu de faire directement 3/5 ÷ 4, on calcule plutôt 3/5 x 1/4, de façon à opérer sur des objets de même nature, un fraction n'étant pas conçu de même nature qu'un nombre entier.

• Division :
  • Deux méthodes étaient principalement employées jusqu'à la fin de la Renaissance
    1. Celle des Arabes (réduire au même dénominateur puis diviser les numérateurs)
    2. La multiplication en croix (1545) :



(Smith. D.E., Hist. of Mathematics, t. 2, p. 227. Manuscrit anonyme datant de 1545.)

Exercices : Pouvez-vous reconnaître les nombres qui apparaissent dans ces exemples ? Quels rapprochements peut-on faire avec l'exemple de Pacioli ci-dessus ?

• Après la Renaissance : Multiplication par l'inverse

Déjà présente chez les Arabes du Maghreb, elle revendra en Europe avec Michael Stifel, en 1544, mais ne sera utilisée plus largement qu'à partir du XVII^e siècle.

Les fractions décimales

Les antécédents

Pour le commerce, les fractions ordinaires et leur notation semble avoir été suffisant au Moyen Âge et à la Renaissance. Les fractions impliquées n'étaient jamais très compliquées, numérateur et dénominateur à trois chiffres au maximum. Toutefois, les maîtres d'abaque de la Renaissance, avec leur besoin de se démarquer de leurs collègues, font référence dans leurs traités à des fractions de plus en plus complexes, avec des numérateurs et dénominateurs de plus de 10 chiffres parfois.

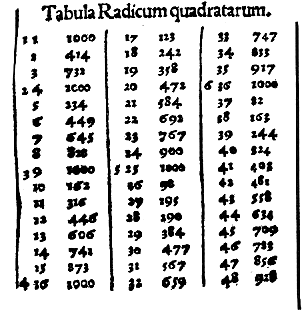
La règle des zéros : Comme chez les Arabes, on trouve des mathématiciens qui utilisent la règle des zéros pour extraire des racines (voir la règle des zéros), comme dans la table des racines carrées d'Adam Reise publiée en 1522, dont les valeurs des racines doivent être divisées par 1000 pour correspondre à la valeur véritable des racines. (Pouvez-vous interpréter la table ? ) :

(Smith, D.E., History of Mathematics, t. 2, p. 237)

Ce genre d'utilisation de la multiplication par 10 se retrouve aussi dans les tables de trigonométries calculer à partir de cercles de rayons de la forme 60 x 10^n.

La règle de division de Regiomontanus (1436-1476). Un règle pour diviser les nombres de la forme a x 10ⁿ. C'est en donnant des exemples de cette règle que Pellos, en 1492, utilise un point pour séparer la partie décimale de la partie entière. Mais ce n'est pour lui qu'un artifice qui n'aura pas de suite. D'ailleurs, les réponses ne sont pas données sous une forme de fractions décimales.

Exercice : en examinant la page illustrée ci-dessous, trouvez comment fonctionne la division de Regiomontanus.

(Smith, D.E., History of Mathematics, t. 2, p. 239)

L'introduction des fractions décimale en Europe

Nous avons vu règle des zéros que les Arabes ont inventé les fractions décimales. Un usage systématique des fractions décimales en Europe ne se présente qu'au XVI^e siècle, avec Christoff Rudolff (1499-1545), dans son Exempel Büchlin de 1530, où il traite de problèmes d'intérêt composé. Ici, la barre est utilisée pour séparer la partie entière de la partie fractionnaire. Mais son travail n'est très apprécié et l'usage des fractions décimale reste très marginal.

L'oeuvre maîtresse pour la popularisation de l'usage des fractions décimales est celui de Simon Stevin (1548-1620), La Disme, paru en 1585 d'abord en flamand puis, la même année, en français. En voici un extrait de la première page de la version française (version de 1634).

La notation de Stevin s'inspire de celle qu'il utilise en algèbre, comme on le constate dans l'extrait suivant (toujours de 1634) :

Ce symbolisme ne fut toutefois pas très populaire. On le trouve tout de même dans une traduction flamande de 1626 d'un livre de Napier.

Le point décimal commencent à être utilisé vers la toute fin du XVI^e siècle. Le point de Pellos (voir ci-haut) ne peut être considérer comme un véritable point décimal, n'étant pas intégré à une véritable pratique de la fraction décimale. Certains auteurs du XVII^e siècle attribuent le premier usage du point décimal à Joost Bürgi (1552-1632). Un de ses manuscrits de 1592 nous font voir un usage systématique du point décimal. Mais c'est avec le XVII^e siècle que son usage se répand. On le rencontre en 1612 dans les tables trigonométriques de Pitiscus (1561-1613), l'inventeur du mot trigonométrie. Napier sera celui par qui l'usage du point se répand, à cause de la dissémination des calculs à l'aide des logarithmes. Néanmoins, beaucoup d'autres symbolisme sont simultanément utilisés, particulièrement certains issus de la notation des fractions sexagésimales appliquée aux fractions décimales (ex. 314,1'5''9'''2''''6'''''5'''''', pour notre 314,159265. Johan Hartmann Beyer (1563-1625) en 1616 dans une lettre à Kepler).

Haut de la page