MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Géométrie (1)
Chapitre trois et quatre de Mankiesicz
Du nombre et de la géométrie
(Chapitres trois et quatre de Mankiesicz)
-
Deux exemples tirés du quotidien
-
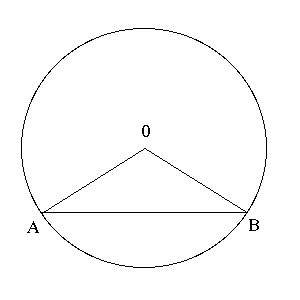
D'où vient que le cercle est divisé en
360º ?
-
D'où vient que la journée est divisée en
24 heures ?
Voir l'article en format pdf ici
(230 Kb)
Dans ces deux cas, il y a passage du
numérque au géométrique. Notez aussi le rôle
"homogénéisant" de la vision géométrique de notre
environnement.
-
L'aire du cercle chez les Égyptiens
Pour calculer l'aire, soustrais au
diamètre son neuvième et élève ce que tu obtiens au
carré
Commnet a-t-on trouver une telle méthode
?
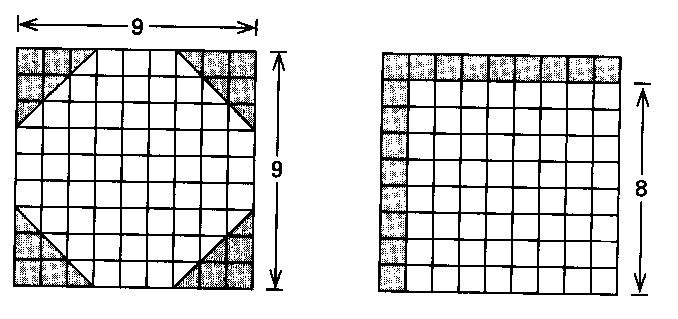
(Katz, V., history of Mathematics, Addison-Wesley,
1998, p. 21)
Du nombre et de la géométrie
(Chapitres trois et quatre de Mankiesicz)-
Deux exemples tirés du quotidien
-
D'où vient que le cercle est divisé en 360º ?
-
D'où vient que la journée est divisée en 24 heures ?
Voir l'article en format pdf ici (230 Kb)
Dans ces deux cas, il y a passage du numérque au géométrique. Notez aussi le rôle "homogénéisant" de la vision géométrique de notre environnement.
-
L'aire du cercle chez les Égyptiens
Pour calculer l'aire, soustrais au diamètre son neuvième et élève ce que tu obtiens au carré
Commnet a-t-on trouver une telle méthode ?

(Katz, V., history of Mathematics, Addison-Wesley, 1998, p. 21)
-
Les Babylonniens aiment les constantes : 0;30 et 0;5 !
L'air du cercle : Calcule le produit de la moitié du diamètre par la moitié de la circonférence

ou
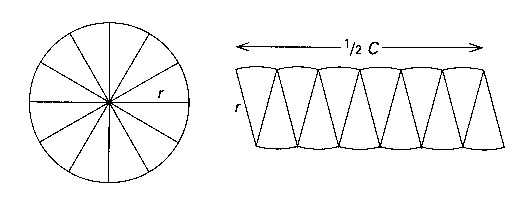
(Katz, V., History of Mathematics, Addison-Wesley, 1998, p. 22)
La géométrie en Grèce
-
La vision grecque du monde
-
Vision cyclique de l'histoire
-
La discussion et le combat
-
Dévalorisation de la pratique
-
Pythagore de Samos (582-497 ???), l'élève de Thalès de Milet (624-548 av. notre ère)
(Pour la section sur Pythagore et celle sur Platon et Aristote : un texte en format pdf (421 kb). Ce texte sera utile pour les questions d'astronomie que nous verrons lors des cours sur la trigonométrie)
-
Tout est nombre.
Le quadrivium (arithmétique, harmonie, géométrie, astronomie) -
Les nombres polygonaux, premières démonstrations ?
-
Découverte des irrationnels : la débandade des pythagoriciens.
-
Peut-on mesurer un angle ?
Le vocabulaire pythagoricien aujourd'hui :
Médecine : ton, tonique, tonus, tempérament
Religion : théorie
Arithmétique : "figure" (en anglais)
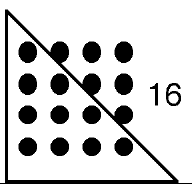
(Section basée sur un article dans le Bulletin AMQ, mars 1987, pp. 5-6 et 46: format pdf ici (280 Kb) )
Première mesure d'angles : confusion de l'espace et du temps, astronomie.
Angle figure : Classification des angles (avant Euclide... et après, Pappus (env. 300 de notre ère))
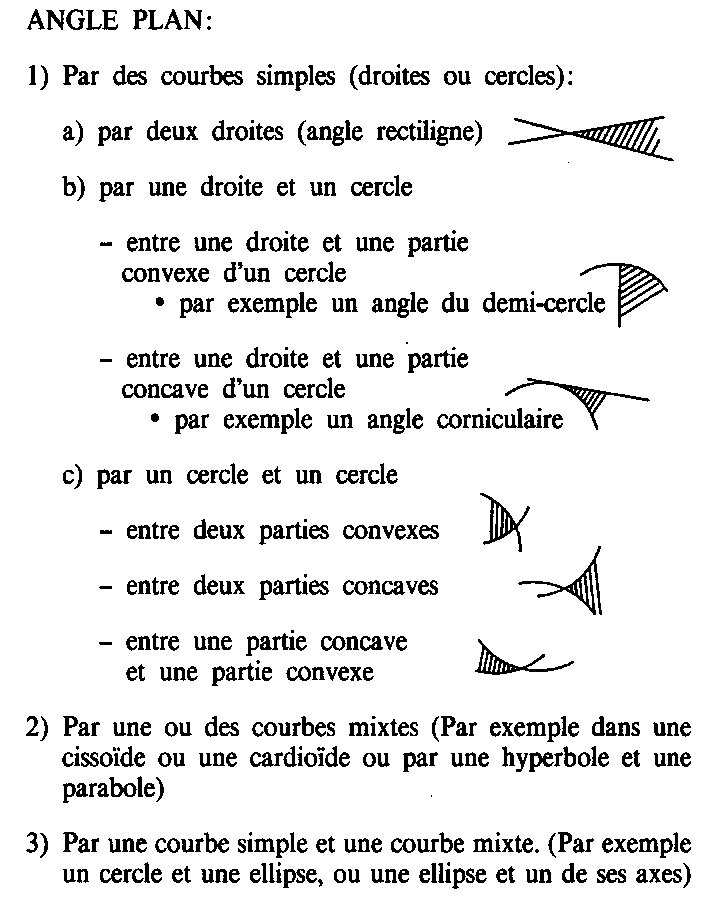
Difficultés relatives à l'angle corniculaire : il n'est pas archimédien.
Angle comme une brisure
Une démonstration d'Aristote :Dans un triangle isocèle, les angles à la base sont égaux.(Isocèle : du grec iso (égal) et skelos (jambes) )
Angle comme inclinaison de deux lignes
Euclide (v. 300 av. notre ère) : Éléments, livre 1, déf. 8 et 9Définition 8 : Un angle plan est l'inclinaison mutuelle de deux lignes qui se touchent dans un plan, et qui ne sont point placées dans la mêmee direction.
Définition 9 : Lorsque les lignes, qui comprennent ledit angle, sont des droites, l'angle se nomme rectiligne.
N.B. Un "angle" de 180º n'est pas un angle (cf. déf. 8) selon Euclide.
Angle comme une rotation
Möbius en 1846
Angle comme un ensemble de demi-droites
David Hilbert en 1899 : Soient h et k deux demi-droites différentes d'un plan A, issues d'un point O et appartenant à des droites différentes. L'ensemble des demi-droites h et k est appelé un angle.
Donc, définir un concept, en apparence aussi simple que l'angle, pose problème !
-
Vers Euclide :
Platon (427-347 av. notre ère) et son élève rebèle Aristote (384-382 av. notre ère), le précepteur d'Alexandre le Grand (356-323 av. notre ère)
(Pour la section sur Pythagore et celle sur Platon et Aristote : un texte en format pdf (421 kb). Ce texte sera utile pour les questions d'astronomie que nous verrons lors des cours sur la trigonométrie)
Platon : L'Académie (fondée en -387, fermée en 529 par l'empereur byzantin Justinien)
Le monde des idées (ou des formes), théorie de la réminiscence.
Aristote : l'expérience, l'homme crée ses idées.
-
Euclide (vers 300 de notre ère)
-
Structure des Éléments
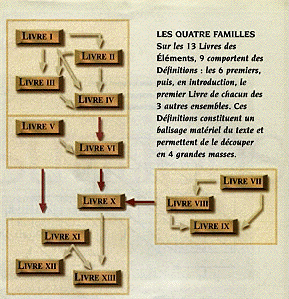 .
.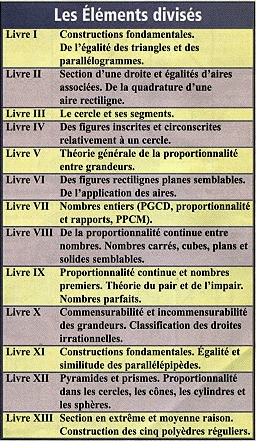
Tiré de l'article de Bernard Vitrac, Les treize Livres d'Euclide, dans Les Cahiers de Science & Vie, Mathématiques, Ce que les Grecs ont vraiment inventé, no 55, Février 2000, p. 50 à 56.
-
Les définitions, axiomes (Notions communes) et postulats (Demandes) :
Télécharger ici (495 Kb) le fichier pdf contenant les définitions, axiomes et postulats, et les premières propositions et le début du livre V et du livre XII. -
Le livre I
Proposition 1 Sur une droite donnée, construire un triangle équilatéral.
Proposition 2 Placer à un point donné un segment de droite égal à une droite donnée.
Proposition 3 Étant donné deux segments de droites inégaux, enlever du plus long un segment de droite égal au plus court.
Proposition 4 Si deux triangles ont deux côtés égaux à deux côtés respectivment, et ont leur angle contenu dans ces côtés égaux l'un à l'autre, le triangle sera égal au triangle et les autres angles seront égaux respectivement c'est-à-dire sous-tendant les côtés respectifs.
Proposition 5 Dans un triangle isocèle, les angles à la base sont égaux et si les côtés sont prolongés, les angles sous la base seront égaux l'un à l'autre.
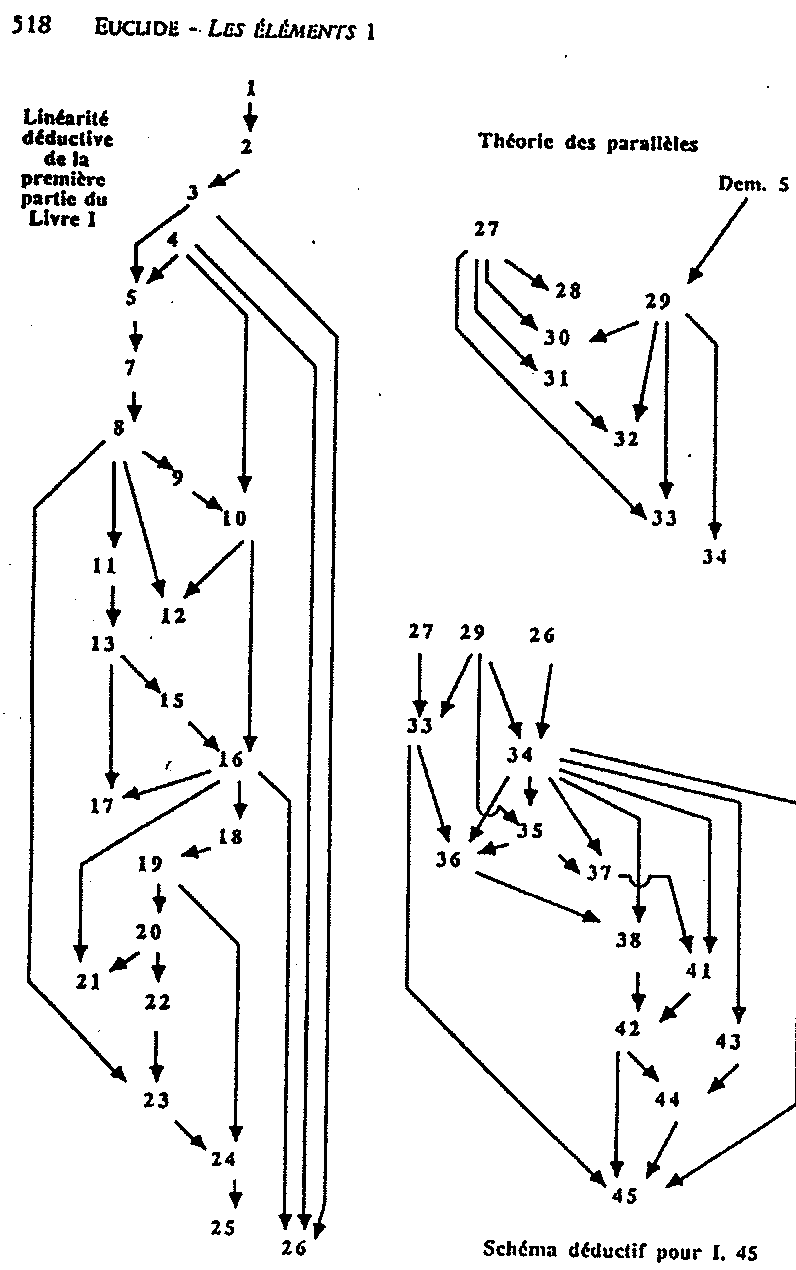
Tiré de Euclide, Les Éléments, vol. 1, Introduction générale, Livre I à IV, Introduction générale ar Maurice Caveing, trad. et comm. par Bernard vitrac, Paris : P.U.F., 1990, p. 518. Reproduit dans le recueil à la page 234.
-
Le livre II
Proposition 1 Étant donné deux segments de droites, si l'un d'eux est divisé en plusieurs segments, le rectangle contenu par les deux droites est égal aux rectangles contenu par le segment non coupé et chacun des autres segments. [a(b+c+d+ ...) = ab + ac + ad + ...]
Proposition 5 Si une droite est coupée en segmentts égaux et inégaux, le rectangle contenu dans les segments inégaux du tout avec le carré sur le segment entre les points de coupure sont égaux au carré sur la demi. [ ab + ((a-b)/2)2 = ((a+b)/2)2, x(d-x) = f2 ]
Proposition 6 Si une droite est coupée en deux parties égales et une droite est ajoutée, le rectangle contenu dans le segment total et le segment ajouté ensemble avec le carré sur la demie est égal au carré sur la demie ajoutée du segment. [ ab + ((a-b)/2)2 = ((a+b)/2)2, x(d+x) = f2 ]
-
Livre V : la théorie des proportions.(Voir les extraits à télécharger ci-haut)
Un site intéressant : Les Éléments, avec une vision "géométrique" avec des couleurs :
-
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |