MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
La trigonométrie (1)
Les systèmes du monde
La trigonométrie
Une ligne du temps
(par Claude Marsollais)
La trigonométrie
Une ligne du temps
(par Claude Marsollais)
(par Claude Marsollais)
-
Hipparque (v. 180-125)
-
Tables de cordese et utilisation d'identités. travaux perdus.
-
-
Ménélaus
-
Théorème sur les sécantes. Début de la trigonométrie sphérique.
-
-
Ptolémée (v. 100)
-
Auteur de l'Almagest : Tables de cordes et identités trigonométriques.
-
-
Théon d'Alexandrie (v. 400)
-
Commentaires d'Hipparque. tables de cordes.
-
-
En Inde
-
Définition du sinus à partir de la corde
-
-
Monde arabe (vers 900 et +)
-
Les "fonctions" trigonométriques, toujours à partir de la corde !
-
Nasir Eddin (1201-1274) : Premier traitié de trigonométrie, sans rapprot avec l'astronomie
-
-
Régiomontanus (en 1464)
-
Trigonométrie du triangle. Loi du sinus explicite, usage dans la trigonométrie sphérique.
-
-
Rhéticus (l'élève de Copernic) (1550)
-
Définition des rapports trigonométriques dans un triangle
-
-
Thomas Finche (1583)
-
Première utilisation du mot tangente
-
-
Pitiscus (1595)
-
Première utilisation du mot « trigonométrie » (en relation avec les triangles)
-
-
François Viète (1540-1603)
-
Redécouverte algébrique des identités
-
-
Edmound Gunter (1620)
-
Première utilisation des termes cosinus et cotangente
-
-
Vers 1700 et après
-
Fonction trigonométriques définies en termes de séries. Relation avec les nombres complexes et les logarithmes.
-
-
Joseph Fourier (1768-1830)
-
Représentation des fonctions par des série de Fourier (séries trigonométriques)
-
Les systèmes du monde
Les systèmes du monde
Avant les Grecs
Les modèles grecs
Le modèle de Ptolémée
(voir les notes de
FSM 3000 (format pdf, 420 kb))
Sauf mention contraire, dans cette section, toutes les
figures proviennent de
Thomas S. Kuhn, The Copernician Revolution, Planetary
Astronomy in the Development of Western Thought, Harvard
Un. Press, 1957.
1.5.1.a Mouvements apparents du Soleil,
des planètes et des étoiles.
i- Mouvements du
Soleil
Avant les Grecs
Les modèles grecs
Le modèle de Ptolémée
(voir les notes de FSM 3000 (format pdf, 420 kb))
Sauf mention contraire, dans cette section, toutes les
figures proviennent de
Thomas S. Kuhn, The Copernician Revolution, Planetary
Astronomy in the Development of Western Thought, Harvard
Un. Press, 1957.
1.5.1.a Mouvements apparents du Soleil, des planètes et des étoiles.
i- Mouvements du Soleil
-
Le Soleil traverse le ciel en 1/2 jour environ. L'hiver, il est visible moins longtemps que l'été
-
Il ne traverse pas toujours le ciel de la même façon. L'hiver, il monte moins haut au-dessus de l'horizon que l'été. Ainsi, l'ombre d'un gnomon à midi n'est pas la même tout au long de l'année (fig. 2 : l'ombre d'un gnomon change d'une saison à l'autre).
-
Cette variation de l'ombre diffère aussi selon la latitude où l'on se trouve.
ii- Mouvements des étoiles et du Soleil
-
Les étoiles se déplacent en bloc et reviennent à la même place toutes les 24 heures environ.
-
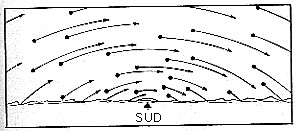
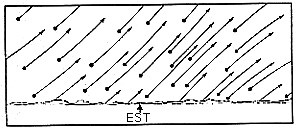
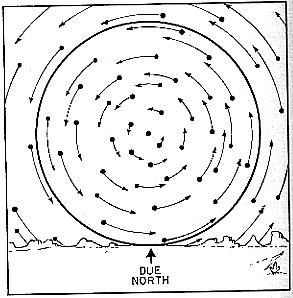
Leurs mouvements sont particuliers, selon qu'on regarde vers le nord, le sud, l'est ou l'ouest
 |
|
-
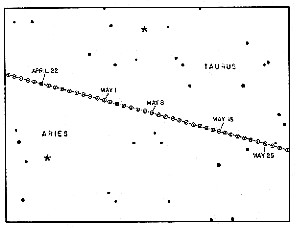
Au crépuscule et à l'aurore, on peut voir en même temps le Soleil et les étoiles les plus brillantes de la voûte étoilée. On peut alors situer le Soleil par rapport aux autres étoiles. Au cours de l'année, le Soleil n'est pas toujours à la même place sur ce fond. Il se déplace lentement vers l'est à travers les constellations du zodiaque.
iii- Mouvements apparents des planètes.
-
Sept étoiles mobiles : les planètes
-
Les orbites des planètes sont toutes approximativement dans le même plan
En examinant quotidiennement la voûte étoilée, on remarque 7 'étoiles' qui changent progressivement de position par rapport aux autres étoiles fixes. Ces 'étoiles' sont le Soleil, la Lune, Mercure, Vénus, Mars, Jupiter, Saturne.
-
Les temps de translation varient, mais ils sont en moyenne constants
Chaque planète parcourt le zodiaque en entier en un temps qui lui est propre. L'intervalle de temps mis par une planète pour revenir à une position donnée varie d'une fois à l'autre de façon presque imprévisible. Par ailleurs, la moyenne de ces intervalles de temps (temps de translation) est constante (Exemple : En moyenne, la lune revient à un même point du zodiaque tous les 29 1/3 jours, mais le temps entre chaque retour peut varier jusqu'à 7h. de cette moyenne en plus ou moins).
-
Les planètes inférieures: Mercure et Vénus
Mercure et Vénus ne s'éloignent jamais beaucoup du Soleil.
-
Le mouvement de rétrogradation des planètes
Les mouvements apparents des planètes, sauf ceux du Soleil et de la Lune, sont entachés d'une autre irrégularité, la rétrogradation.
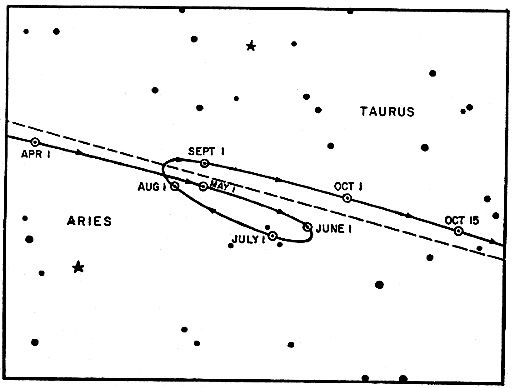
a) Les rétrogradations se font à des intervalles à peu près réguliers, mais pas toujours aux mêmes endroits dans le ciel.
b) Pour les planètes Mars, Jupiter et Saturne, elles se font lorsque
i) la planète est en opposition avec le Soleil (donc la planète, la Terre et le Soleil sont alignés, dans cet ordre),
ii) l'intensité lumineuse de la planète est alors à son maximum. Donc on peut croire qu'elle est plus près de la Terre qu'à d'autres moments.
Les planètes ne s'éloignent jamais de plus de 8° de l'écliptique (zodiaque).
iv- Le modèle des 2 sphères. (les sphères armillaires vues en classe)
1-Les étoiles sont placées sur la sphère extérieure. Celle-ci fait un tour complet en 24 heures environ.
2- Le Soleil se déplace entre la sphère des étoiles et la Terre (elle-même une petite sphère au centre de la sphère des étoiles). Vu de la Terre, le Soleil est perçu comme étant sur la sphère des étoiles.
3-L'image du Soleil sur le fond étoilé décrit en un an un grand cercle. Ce cercle est l'écliptique. Il fait un angle de 23 1/2° avec l'équateur de la sphère des étoiles.
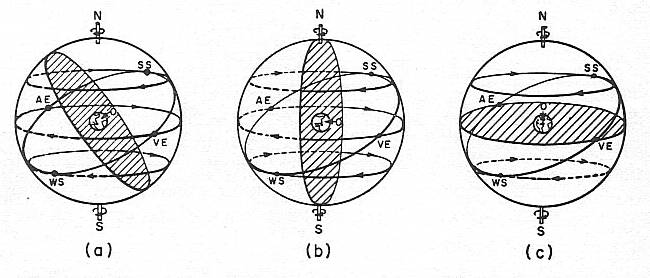
Ce modèle permet de prévoir les mouvements apparents du Soleil sur la sphère des étoiles : l'heure de son lever, sa course pour quelque jour que ce soit, sous quelque latitude que ce soit. (La démonstration faite en classe)
(a) Mouvement du Soleil à une latitude moyenne
(b) Mouvement du Soleil à l'équateur
(c) Mouvement du Soleil au Pôle Nord
Pour les mouvements des planètes, le modèle ne permet de faire aucune prédiction. Rappelons que la cosmologie aristotélicienne tente de retrouver approximativement ces mouvements par le frottement entre les sphères. Mais il ne réussit guère à reproduire la diversité des mouvements planétaires.
1523 : Raymond Lull, Practica compendiosa
artis.
Hugh Kearney, Science and Change, 1500-1700, New York :
McGraw-Hill, p. 31.
1.5.2 Les solutions proposées par Ptolémée
1.5.2.a Le modèle ptoléméen
i- Description du modèle
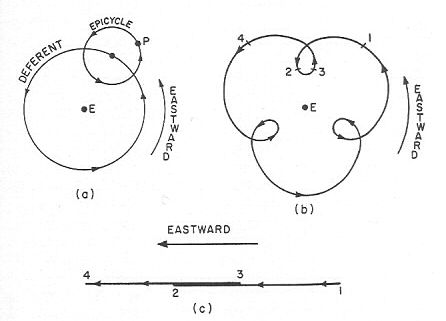
Le modèle de Ptolémée ne concerne véritablement que les planètes et le Soleil. En ce qui a trait aux étoiles, il s'en tient au modèle des deux sphères. Pour décrire le mouvement des planètes, il a recours à la combinaison à deux mouvements circulaires. Chaque planète est située sur un petit cercle, appelé épicycle, dont le centre est lui-même placé sur autre cercle, appelé déférent, centré près du centre de l'univers. Idéalement, les deux cercles ont chacun une vitesse angulaire constante. Selon les rapports des vitesses angulaires des deux cercles et selon les rapports des rayons des cercles, la planète décrira une trajectoire particulière. Dans ci-dessous, l'épicycle tourne à une vitesse angulaire trois fois plus grande que la vitesse angulaire du déférent.
Figure 19
On peut aussi voir deux films (Quicktime) provenant du cours FSM 3000 (sur internet) de l'UQAM:
Les épicycles d'Hipparque (1.35 meg) -- Les ajustements de Ptolémée (635 kb)
Ptolémée est assez clair sur les objectifs qu'il s'est donnés:
Nous croyons que le but que l'astronome doit s'efforcer d'atteindre est le suivant : démontrer que tous les phénomènes du ciel sont produits par des mouvements circulaires et uniformes. (... ) Nous étant fixé la tâche de prouver que les irrégularités apparentes des cinq planètes, du Soleil et de la Lune peuvent être toutes représentées au moyen de mouvements circulaires uniformes, parce que seuls ces mouvements sont appropriés à leur nature divine... nous sommes en droit de regarder l'accomplissement de cette tâche comme le but ultime de la science mathématique basée sur la philosophie.
L'on voit donc que Ptolémée fait sienne la dichotomie entre le monde terrestre et le monde céleste. L'influence platonicienne et aristotélicienne est claire. Aristote lui donne la structure globale du monde. Platon lui donne la justification de traiter purement idéalement les planètes. Il n'y a pas de physique impliquée ici. Les êtres célestes font partie du monde des idées. Nous pouvons les connaître par la géométrie. Mais leur nature nous est inaccessible.
ii- Explications des mouvements apparents des planètes ?
Les orbites des planètes sont toutes approximativement dans le même plan
Le système ne reproduit pas ce phénomène de lui-même. Cependant, on peut disposer les plans des orbites de sorte qu'ils forment avec le plan de l'écliptique un angle d'au plus 8°. Mais il s'agit là d'une décision de celui qui détermine les paramètres du système. Ce choix vise à faire en sorte que les prédictions du système correspondent aux observations. Cette correspondance est tributaire du degré de précision que s'impose celui qui fixe ces paramètres.
Les temps de translation varient, mais sont en moyenne constants
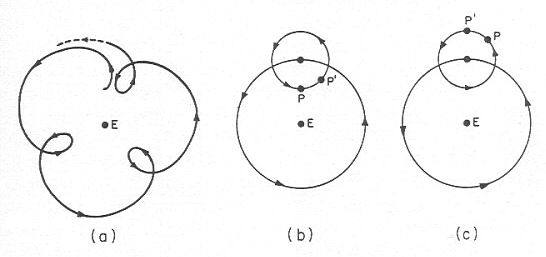
Voir les figures ci-dessous - 20 b) et c). Le système reproduit de lui-même une variation des temps de translation. La moyenne des temps de translation est le temps pris par le déférent pour faire un tour complet autour de la Terre. Il y a des paramètres à fixer pour chacune des planètes: rayons du déférent et de l'épicycle, rapport des vitesses angulaires, position du centre de l'univers.
Figure 20
Les planètes inférieures: Mercure et Vénus
Le système ne reproduit pas ce phénomène de lui-même. Il faut lui imposer que le centre de l'épicycle d'une planète inférieure, le centre de la Terre et celui du Soleil soient à tout moment colinéaires.
Figure 21
Le mouvement de rétrogradation des planètes
a) Intervalle entre les rétrogradations
Voir les figures précédentes b) pour l'avant dernière, et a) pour celle ci-dessus. Le système reproduit par lui-même le phénomène de rétrogradation. Toutefois, selon le système, le temps entre les rétrogradations est toujours le même. Le temps et la position entre deux rétrogradations sont déterminés par le rapport des vitesses de rotation de l'épicycle et du déférent. L'étalement de la rétrogradation est fonction du rapport des rayons du déférent et de l'épicycle.
b) Particularités pour les planètes Mars, Jupiter et Saturne:
i) Pour qu'au moment de la rétrogradation la planète soit nécessairement en opposition avec le Soleil, il faut imposer des contraintes aux paramètres de la planète.
ii) En choisissant adéquatement le sens de rotation de l'épicycle par rapport au sens de rotation du déférent, les boucles de l'orbite se font vers le centre du déférent, en l'occurrence la Terre. Alors, l'intensité lumineuse de la planète devrait sembler plus intense vue de la Terre. Dans la figure 19, si l'épicycle tournait dans l'autre sens, les boucles se feraient vers l'extérieur.
iii- Mouvements non décrits par le système ptoléméen
a) Comme nous l'avons dit ci-dessus, selon le système, les intervalles de temps entre les rétrogradations devraient être égaux. Ce n'est pas le cas en réalité.
b) En réalité, les planètes inférieures n'atteignent pas toujours la déviation maximale prévue par le système. (Voir la figure 21 a).
c) Le temps pris par le Soleil pour aller d'un équinoxe à l'autre (équinoxe: moment où le Soleil est à l'un des points communs à l'équateur céleste et à l'écliptique. Il y a deux équinoxes: l'équinoxe du printemps, l'équinoxe d'automne). La vitesse angulaire du Soleil est légèrement plus rapide en automne et en hiver qu'au printemps et en été. Autrement dit, le temps pris par le Soleil pour aller de l'équinoxe d'automne à l'équinoxe du printemps est moins long que celui pris pour aller de l'équinoxe du printemps à l'équinoxe d'automne. Or, puisque le Soleil n'a pas de rétrogradation, il ne devrait pas avoir besoin d'un épicycle. Dans ce cas les temps entre les équinoxes devraient être rigoureusement égaux.
iv- Mécanismes correctifs
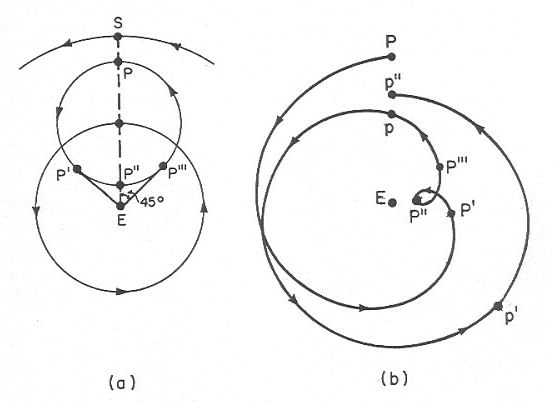
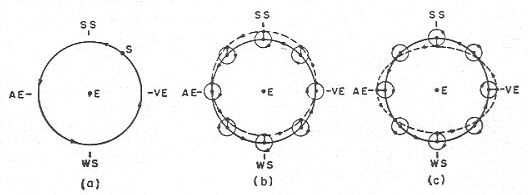
Des mécanismes correctifs ont dû être développés pour tenir compte de ces mouvements. Ils introduisent toutefois des incongruités dans le système. Par exemple, pour l'inégalité des temps entre les équinoxes, Ptolémée ajoute au Soleil un épicycle mineur dont le rayon est très petit par rapport au rayon du déférent. La figure 22 b montre qu'en égalant la vitesse angulaire de l'épicycle à celle du déférent, mais dans le sens opposé, le Soleil met plus de temps à aller de l'équinoxe d'automne à l'équinoxe du printemps que pour compléter son périple de l'équinoxe du printemps à l'équinoxe d'automne. De fait, l'orbite du Soleil est alors un cercle dont le centre est déplacé du côté de l'été.
Figure 22
La figure 24 illustre un autre mécanisme correctif. Il s'agit de déplacer légèrement le centre du déférent de sorte qu'il ne soit pas confondu avec le centre de la Terre, centre de l'univers. Le centre du déférent peut tourner si nécessaire autour de la Terre. (Voir l'illustration de l'orbite ovale de Mercure qui accompagne les figures des cosmologies égyptienne et grecques.) Ainsi, dans le modèle de Ptolémée, chaque planète tourne autour d'un centre qui lui est propre et qui est toujours différent du centre de la Terre qui se confond avec le centre de l'univers.
Figure 24
Le système de Copernic
3.2.1.b Son système
i- Description du système
Le système de Copernique repose, comme celui
de Ptolémée, sur le système des deux sphères. Il y a deux
différences essentielles toutefois.
D’abord, ce n’est plus la Terre qui est
immobile au centre, mais le Soleil. Toutes les planètes,
sauf la Lune, mais y compris la Terre, tournent autour du
Soleil. La Terre a trois mouvements:
i) mouvement diurne : rotation autour de
son axe en une journée,
ii) translation: mouvement annuel autour du
Soleil,
iii) mouvement annuel de rotation de l'axe
de la Terre ( voir la figure 31 b).
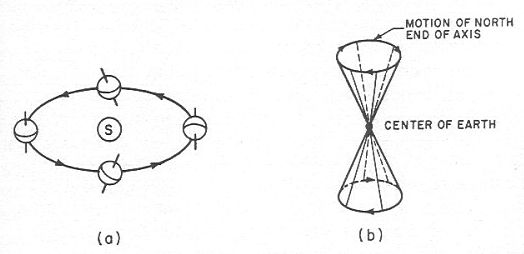
Figure 31
Le mouvement de rotation de l’axe de la Terre
vise à assurer que cet axe conserve toujours la même
orientation. Copernique croyait, en homme de son temps, que
la Terre se comportait, en tournant autour du Soleil, comme
si elle était reliée au Soleil par une tige de sorte que
l’orientation de l’axe de la Terre était toujours la même
par rapport au Soleil (voir la figure 31a). Dès lors, l’axe
de la Terre doit tourner en un mouvement annuel de façon à
ce que l’axe soit toujours dans la même direction absolue.
Ce n’est qu’à ce prix que les variations des mouvements
apparents du Soleil selon les saisons sont reproduites par
le système.
Deuxième différence, la sphère céleste est
immobile et très grande.
ii- Explication des mouvements apparents.
-
-
Le mouvement diurne du soleil et des
étoiles
La rotation journalière de la Terre sur son axe produit,
pour un observateur terrestre, un mouvement apparent de
rotation sur la sphère des étoiles. (Voir la figure 28)
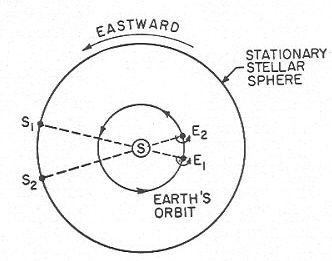
Figure 28
-
-
Les changements du mouvement diurne du
Soleil selon les saisons.
En assurant, par l’ajout du mouvement annuel de rotation
de l’axe de la Terre, que cet axe pointe toujours dans
la même direction absolue, le mouvement diurne du Soleil
change selon les saisons étant donné que, par rapport au
Soleil, l’axe change d’orientation. (Voir la figure 29.)
Il est à noter que, la Terre se déplaçant autour du
Soleil, la position des étoiles à un moment de l’année
devrait être affectée par la position de la Terre. Ce
phénomène s’appelle la parallaxe. (Voir la figure 30)
Ainsi, l’étoile polaire, que l’on voit toute l’année, ne
serait pas à la même hauteur angulaire toute l’année. Or
de tels changements, pour quelque étoile que ce soit,
n’ont jamais été observés. Il s’ensuit que les étoiles
doivent être très éloignées de la Terre.
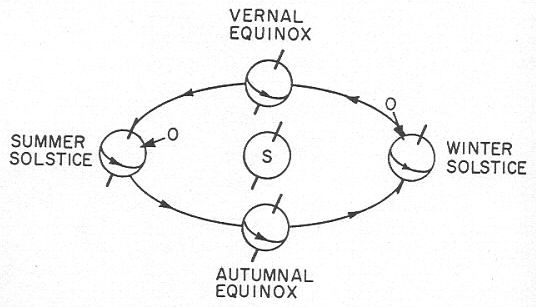
Figure 29
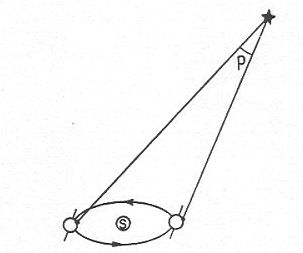
Figure 30
Le système de Copernic
3.2.1.b Son système
i- Description du système
Le système de Copernique repose, comme celui de Ptolémée, sur le système des deux sphères. Il y a deux différences essentielles toutefois.
D’abord, ce n’est plus la Terre qui est immobile au centre, mais le Soleil. Toutes les planètes, sauf la Lune, mais y compris la Terre, tournent autour du Soleil. La Terre a trois mouvements:
i) mouvement diurne : rotation autour de son axe en une journée,
ii) translation: mouvement annuel autour du Soleil,
iii) mouvement annuel de rotation de l'axe de la Terre ( voir la figure 31 b).
Figure 31
Le mouvement de rotation de l’axe de la Terre vise à assurer que cet axe conserve toujours la même orientation. Copernique croyait, en homme de son temps, que la Terre se comportait, en tournant autour du Soleil, comme si elle était reliée au Soleil par une tige de sorte que l’orientation de l’axe de la Terre était toujours la même par rapport au Soleil (voir la figure 31a). Dès lors, l’axe de la Terre doit tourner en un mouvement annuel de façon à ce que l’axe soit toujours dans la même direction absolue. Ce n’est qu’à ce prix que les variations des mouvements apparents du Soleil selon les saisons sont reproduites par le système.
Deuxième différence, la sphère céleste est immobile et très grande.
ii- Explication des mouvements apparents.
-
Le mouvement diurne du soleil et des étoiles
La rotation journalière de la Terre sur son axe produit, pour un observateur terrestre, un mouvement apparent de rotation sur la sphère des étoiles. (Voir la figure 28)

Figure 28
-
Les changements du mouvement diurne du Soleil selon les saisons.
En assurant, par l’ajout du mouvement annuel de rotation de l’axe de la Terre, que cet axe pointe toujours dans la même direction absolue, le mouvement diurne du Soleil change selon les saisons étant donné que, par rapport au Soleil, l’axe change d’orientation. (Voir la figure 29.) Il est à noter que, la Terre se déplaçant autour du Soleil, la position des étoiles à un moment de l’année devrait être affectée par la position de la Terre. Ce phénomène s’appelle la parallaxe. (Voir la figure 30) Ainsi, l’étoile polaire, que l’on voit toute l’année, ne serait pas à la même hauteur angulaire toute l’année. Or de tels changements, pour quelque étoile que ce soit, n’ont jamais été observés. Il s’ensuit que les étoiles doivent être très éloignées de la Terre.

Figure 29
Figure 30
-
Les orbites des planètes sont toutes
approximativement dans le même plan
De manière similaire à ce qui était fait dans le système
de Ptolémée, il suffit de placer le plan de l’orbite de
chacune des planètes de façon à ce qu’il soit incliné à
peu près comme celui de l’orbite de la Terre.
-
Les temps de translation varient, mais
sont en moyenne constants
Le temps mis par la Terre pour faire un tour complet du
Soleil et celui mis par une planète pour faire elle
aussi un tel tour sont différents. On peut voir, figure
33, que si on suppose qu’alors que la planète fait un
tour complet, la Terre fait un tour et un quart, la
planète peut prendre trois positions apparentes
différentes alors qu’elle revient à la même position
absolue. Le temps entre les retours à une même position
apparente varie donc. La moyenne de ces temps est égale
au temps pris par la planète pour revenir à la même
position absolue.
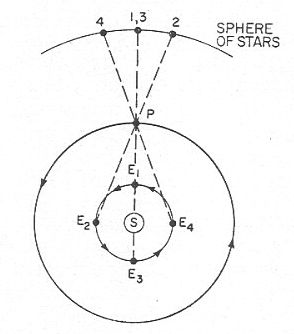
Figure 33
-
Les planètes inférieures: Mercure et
Vénus
Vues de la Terre, les planètes inférieures tournant
autour du Soleil ne s’en éloignent jamais. Le système
reproduit donc naturellement ce mouvement apparent.
-
Le mouvement de rétrogradation des
planètes
a) Intervalle entre les
rétrogradationsComme pour le système de Ptolémée, le
système de Copernique reproduit par lui-même le
phénomène de rétrogradation. Toutefois, alors que
Ptolémée avait dû introduire un élément particulier,
les épicycles, pour que le système génère les
rétrogradations, Copernique n'a qu'à laisser
fonctionner son système pour que les rétrogradations
se produisent. (Voir la figure 32) Qu’en est-il du
temps prévu entre chaque rétrogradation ? Est-il
rigoureusement le même ? Oui.
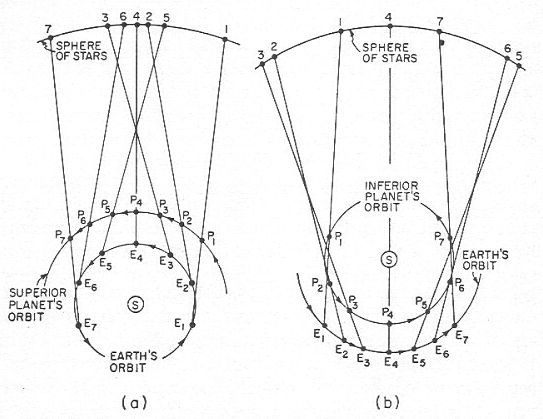
Figure 32
b) Particularités pour les planètes
Mars, Jupiter et Saturne:
i) Dans le système, la
rétrogradation se produit nécessairement au moment
où la Terre et la planète sont le plus proche.
Puisque les orbites sont des cercles
concentriques, la distance minimum entre deux
points de ces cercles est celle qui correspondant
au segment du rayon du cercle extérieur qui se
trouve entre les deux cercles. [C’est le moment où
les directions instantanées des deux planètes sont
parallèles.] (Voir la figure 32)
ii) On a indiqué, en i), que la rétrogradation se
produisait précisément lorsque la Terre se
trouvait le plus près de la planète. La planète
apparaît alors, vue de la Terre, plus lumineuse
qu'en tout autre temps.
iii- Mouvements non décrits par le système
copernicien
a) Les intervalles de temps entre les
rétrogradations devraient être égaux selon le système de
Copernique. Ce n’est pas le cas en réalité. Par rapport
à cette irrégularité, le système de Copernique n'est
donc pas supérieur à celui de Ptolémée.
b) Selon le système de Copernique, les
planètes inférieures devraient toujours atteindre leur
déviation maximale par rapport au Soleil. Encore là, en
réalité, les planètes n’atteignent pas toujours leur
déviation maximale.
c) Le temps pris par le Soleil pour aller
de l’équinoxe d’automne à l’équinoxe du printemps est
moins long que celui pris pour aller de l’équinoxe du
printemps à l’équinoxe d’automne. La Terre tournant sur
un cercle centré au Soleil, le système ne reproduit pas
cette inégalité.
iv- Mécanismes correctifs.
Les mêmes que ceux utilisés par Ptolémée.
(Voir les figures 34)
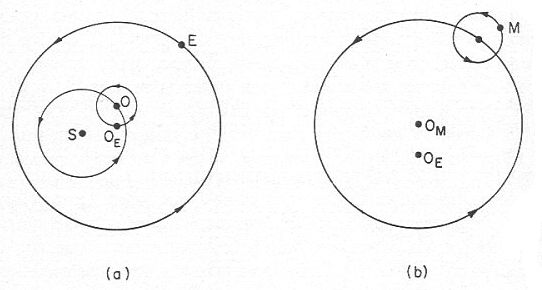
Figure 34
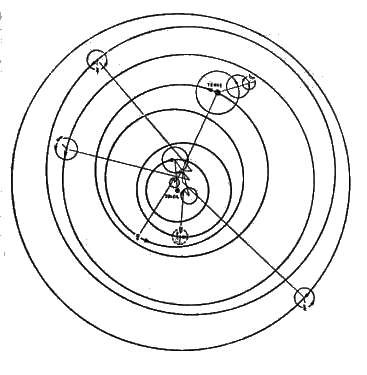
Le modèle de Copernic
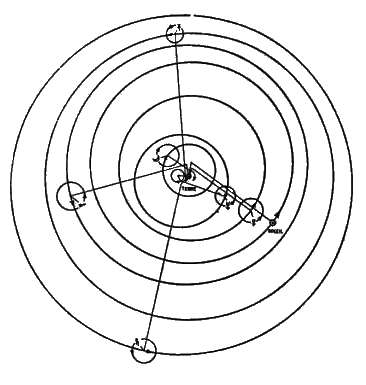
Le modèle de Ptolémée
v- Système de Copernique versus système de
Ptolémée
Le système de Copernique reproduit avec
beaucoup d’économie les phénomènes de rétrogradation et
ses caractéristiques (luminosité, opposition avec le
Soleil). Le fait que les planètes Mercure et Vénus soient
toujours en apparence près du Soleil découle aussi de la
configuration du système. Par ailleurs, la translation de
Vénus autour du Soleil a pour conséquence que Vénus
devrait avoir, comme la Lune, des phases lorsque vue de la
Terre.
Dans le système copernicien, le temps entre
deux rétrogradations permet de calculer l'année
planétaire.
Dans le système de Copernique, il est
possible de calculer la distance entre une planète et le
Soleil. (Voir la figure 36.) Dans le système de Ptolémée,
il n’y a pas moyen de faire un tel type de calcul.
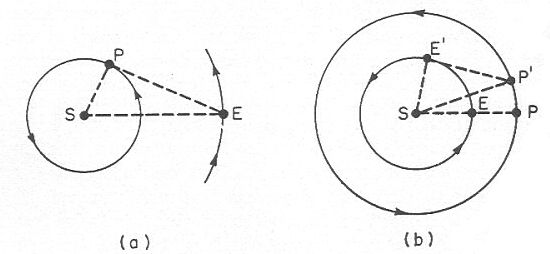
Figure 36
Ce sont là des avantages du système
copernicien. Mais ces avantages sont plus qualitatifs que
quantitatifs. Lorsqu’il s’agit d’ajuster les prédictions
du système aux observations, les mêmes problèmes que ceux
rencontrés par Ptolémée se manifestent. Copernique n’a
alors pas d’autres choix que d’utiliser les artifices mis
au point par Ptolémée (comme de petits épicycles
additionnels). De fait, le système complet de Copernique
comporte 48 cercles alors que celui de Ptolémée n’en
comporte que 40. Au niveau des principes, le système
héliocentrique est nettement plus simple que le système
géocentrique. Au niveau des calculs toutefois, cette
économie s’évapore dans les tentatives d’ajuster le
système aux observations.
N’oublions pas une différence majeure entre
les deux systèmes. Alors que dans le système de Ptolémée
la sphère des étoiles occupe un espace relativement
limité, dans celui de Copernique elle est nécessairement
très grande par rapport à l'orbite de la Terre.
3.2.1.c Les a priori philosophiques
Nous avons signalé, au début de cette
section 3.2.1, quelques difficultés qu’engendre la
cosmologie copernicienne pour les tenants de la cosmologie
d’Aristote. Copernique montre donc une certaine
indépendance d’esprit. Toutefois, il ne peut renier
complètement l’époque dans laquelle il vit. De fait, des
influences aristotéliciennes et néoplatoniciennes sont
nettement décelables chez lui.
Ainsi, pour contrer Aristote , Copernique
argumente de façon aristotélicienne.
a) Les objets tombent sur la Terre (et
non au centre de l’univers où est le Soleil) parce que
les objets ont par nature tendance à former des corps
parfaits.
b) Les objets lancés vers le haut
retombent à la même place que celle d’où ils ont été
lancés parce que la rotation est un mouvement naturel.
Un objet lancé continue donc, une fois laissé à
lui-même, à se mouvoir suivant le mouvement naturel de
rotation de la Terre. De plus, les vents que prévoit
Aristote dans l’éventualité d’un mouvement de rotation
de la Terre ne sauraient se produire car l’air qui
entoure la Terre contient aussi de la terre et de l’eau.
L’air est donc mis en mouvement par le mouvement naturel
de la terre. Le mouvement circulaire naturel de la Terre
devient donc un mouvement naturel pour l’air.
Par ailleurs, nous pouvons percevoir une
référence directe au mouvement néoplatonicien dans un
texte de Copernique. (Voir le texte) De fait, la référence
à Trimegiste suggère aussi un public auquel le livre
s’adresse. Tout ce texte est d’inspiration
néoplatonicienne. Certes Platon lui-même avait placé la
Terre au centre de l’univers et avait attribué à celle-ci
une nature différente de celle des astres célestes. Mais
les néoplatoniciens de la Renaissance retiennent
principalement, dans la foulée des pères de l’Église, que
le monde céleste, monde divin, agit sur nous. L’action du
Soleil est primordiale à la vie sur la Terre. Le Soleil
joue un rôle unique pour les planètes: 1) les planètes
inférieures ne s’en éloignent en apparence jamais, 2) lors
de leurs rétrogradations, les planètes supérieures sont en
opposition avec le Soleil. Comment alors ne pas lui donner
une place spéciale, centrale, dans l’univers?
Le nouveau système intrigue les
contemporains de Copernique. Sur le plan qualitatif, il
est plus économique que celui de Ptolémée. Mais, sur le
plan des calculs, il n’est pas plus efficace, ni plus
conforme aux observations. Toutefois, il plaît aux
néoplatoniciens et en particulier à celui qui est le plus
néoplatonicien de tous, Kepler.
Le modèle de Tycho Brahé
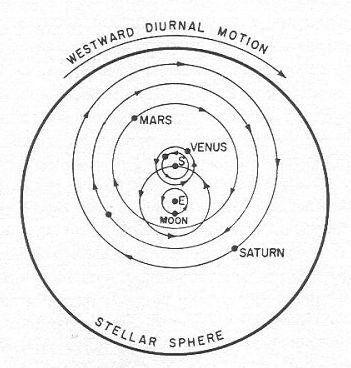
Figure 37
-
Les orbites des planètes sont toutes approximativement dans le même plan
De manière similaire à ce qui était fait dans le système de Ptolémée, il suffit de placer le plan de l’orbite de chacune des planètes de façon à ce qu’il soit incliné à peu près comme celui de l’orbite de la Terre. -
Les temps de translation varient, mais sont en moyenne constants
Le temps mis par la Terre pour faire un tour complet du Soleil et celui mis par une planète pour faire elle aussi un tel tour sont différents. On peut voir, figure 33, que si on suppose qu’alors que la planète fait un tour complet, la Terre fait un tour et un quart, la planète peut prendre trois positions apparentes différentes alors qu’elle revient à la même position absolue. Le temps entre les retours à une même position apparente varie donc. La moyenne de ces temps est égale au temps pris par la planète pour revenir à la même position absolue.Figure 33
-
Les planètes inférieures: Mercure et Vénus
Vues de la Terre, les planètes inférieures tournant autour du Soleil ne s’en éloignent jamais. Le système reproduit donc naturellement ce mouvement apparent. -
Le mouvement de rétrogradation des planètes
a) Intervalle entre les rétrogradationsComme pour le système de Ptolémée, le système de Copernique reproduit par lui-même le phénomène de rétrogradation. Toutefois, alors que Ptolémée avait dû introduire un élément particulier, les épicycles, pour que le système génère les rétrogradations, Copernique n'a qu'à laisser fonctionner son système pour que les rétrogradations se produisent. (Voir la figure 32) Qu’en est-il du temps prévu entre chaque rétrogradation ? Est-il rigoureusement le même ? Oui.
Figure 32
b) Particularités pour les planètes Mars, Jupiter et Saturne:
i) Dans le système, la rétrogradation se produit nécessairement au moment où la Terre et la planète sont le plus proche. Puisque les orbites sont des cercles concentriques, la distance minimum entre deux points de ces cercles est celle qui correspondant au segment du rayon du cercle extérieur qui se trouve entre les deux cercles. [C’est le moment où les directions instantanées des deux planètes sont parallèles.] (Voir la figure 32)
ii) On a indiqué, en i), que la rétrogradation se produisait précisément lorsque la Terre se trouvait le plus près de la planète. La planète apparaît alors, vue de la Terre, plus lumineuse qu'en tout autre temps.
iii- Mouvements non décrits par le système copernicien
a) Les intervalles de temps entre les rétrogradations devraient être égaux selon le système de Copernique. Ce n’est pas le cas en réalité. Par rapport à cette irrégularité, le système de Copernique n'est donc pas supérieur à celui de Ptolémée.
b) Selon le système de Copernique, les planètes inférieures devraient toujours atteindre leur déviation maximale par rapport au Soleil. Encore là, en réalité, les planètes n’atteignent pas toujours leur déviation maximale.
c) Le temps pris par le Soleil pour aller de l’équinoxe d’automne à l’équinoxe du printemps est moins long que celui pris pour aller de l’équinoxe du printemps à l’équinoxe d’automne. La Terre tournant sur un cercle centré au Soleil, le système ne reproduit pas cette inégalité.
iv- Mécanismes correctifs.
Les mêmes que ceux utilisés par Ptolémée. (Voir les figures 34)
Figure 34
Le modèle de Copernic
Le modèle de Ptolémée
v- Système de Copernique versus système de Ptolémée
Le système de Copernique reproduit avec beaucoup d’économie les phénomènes de rétrogradation et ses caractéristiques (luminosité, opposition avec le Soleil). Le fait que les planètes Mercure et Vénus soient toujours en apparence près du Soleil découle aussi de la configuration du système. Par ailleurs, la translation de Vénus autour du Soleil a pour conséquence que Vénus devrait avoir, comme la Lune, des phases lorsque vue de la Terre.
Dans le système copernicien, le temps entre deux rétrogradations permet de calculer l'année planétaire.
Dans le système de Copernique, il est possible de calculer la distance entre une planète et le Soleil. (Voir la figure 36.) Dans le système de Ptolémée, il n’y a pas moyen de faire un tel type de calcul.
Figure 36
Ce sont là des avantages du système copernicien. Mais ces avantages sont plus qualitatifs que quantitatifs. Lorsqu’il s’agit d’ajuster les prédictions du système aux observations, les mêmes problèmes que ceux rencontrés par Ptolémée se manifestent. Copernique n’a alors pas d’autres choix que d’utiliser les artifices mis au point par Ptolémée (comme de petits épicycles additionnels). De fait, le système complet de Copernique comporte 48 cercles alors que celui de Ptolémée n’en comporte que 40. Au niveau des principes, le système héliocentrique est nettement plus simple que le système géocentrique. Au niveau des calculs toutefois, cette économie s’évapore dans les tentatives d’ajuster le système aux observations.
N’oublions pas une différence majeure entre les deux systèmes. Alors que dans le système de Ptolémée la sphère des étoiles occupe un espace relativement limité, dans celui de Copernique elle est nécessairement très grande par rapport à l'orbite de la Terre.
3.2.1.c Les a priori philosophiques
Nous avons signalé, au début de cette section 3.2.1, quelques difficultés qu’engendre la cosmologie copernicienne pour les tenants de la cosmologie d’Aristote. Copernique montre donc une certaine indépendance d’esprit. Toutefois, il ne peut renier complètement l’époque dans laquelle il vit. De fait, des influences aristotéliciennes et néoplatoniciennes sont nettement décelables chez lui.
Ainsi, pour contrer Aristote , Copernique argumente de façon aristotélicienne.
a) Les objets tombent sur la Terre (et non au centre de l’univers où est le Soleil) parce que les objets ont par nature tendance à former des corps parfaits.
b) Les objets lancés vers le haut retombent à la même place que celle d’où ils ont été lancés parce que la rotation est un mouvement naturel. Un objet lancé continue donc, une fois laissé à lui-même, à se mouvoir suivant le mouvement naturel de rotation de la Terre. De plus, les vents que prévoit Aristote dans l’éventualité d’un mouvement de rotation de la Terre ne sauraient se produire car l’air qui entoure la Terre contient aussi de la terre et de l’eau. L’air est donc mis en mouvement par le mouvement naturel de la terre. Le mouvement circulaire naturel de la Terre devient donc un mouvement naturel pour l’air.
Par ailleurs, nous pouvons percevoir une référence directe au mouvement néoplatonicien dans un texte de Copernique. (Voir le texte) De fait, la référence à Trimegiste suggère aussi un public auquel le livre s’adresse. Tout ce texte est d’inspiration néoplatonicienne. Certes Platon lui-même avait placé la Terre au centre de l’univers et avait attribué à celle-ci une nature différente de celle des astres célestes. Mais les néoplatoniciens de la Renaissance retiennent principalement, dans la foulée des pères de l’Église, que le monde céleste, monde divin, agit sur nous. L’action du Soleil est primordiale à la vie sur la Terre. Le Soleil joue un rôle unique pour les planètes: 1) les planètes inférieures ne s’en éloignent en apparence jamais, 2) lors de leurs rétrogradations, les planètes supérieures sont en opposition avec le Soleil. Comment alors ne pas lui donner une place spéciale, centrale, dans l’univers?
Le nouveau système intrigue les contemporains de Copernique. Sur le plan qualitatif, il est plus économique que celui de Ptolémée. Mais, sur le plan des calculs, il n’est pas plus efficace, ni plus conforme aux observations. Toutefois, il plaît aux néoplatoniciens et en particulier à celui qui est le plus néoplatonicien de tous, Kepler.
Le modèle de Tycho Brahé
Figure 37
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |