MAT 6221

Bas de la page

prof. Louis Charbonneau
UQAM

Algèbre (2)


 

6. Vers un symbolisme fonctionnel : La Renaissance

  • Multiplicité des symboles

  • La résolution des équations du 3e degré : Cardan (1501-1576) et les nombres complexes

 

7. François Viète (1542-1603) : l'algèbre obtient ses lettres de noblesses

Extraits de textes de Viète (pdf, 5 Mo)

    Activité : comparez le Zététique IIII, du second livre des Cinq livres des zététiques (Voir les pages ci-dessus). au problème I-XXVII de Diophante.

 

 

 

    Un exemple de l'approche analytique de Viète chez l'un de ses disciples :
    Marino Ghetaldi, De Resolutione et Compositione Mathematica, 1630, Problème VIII

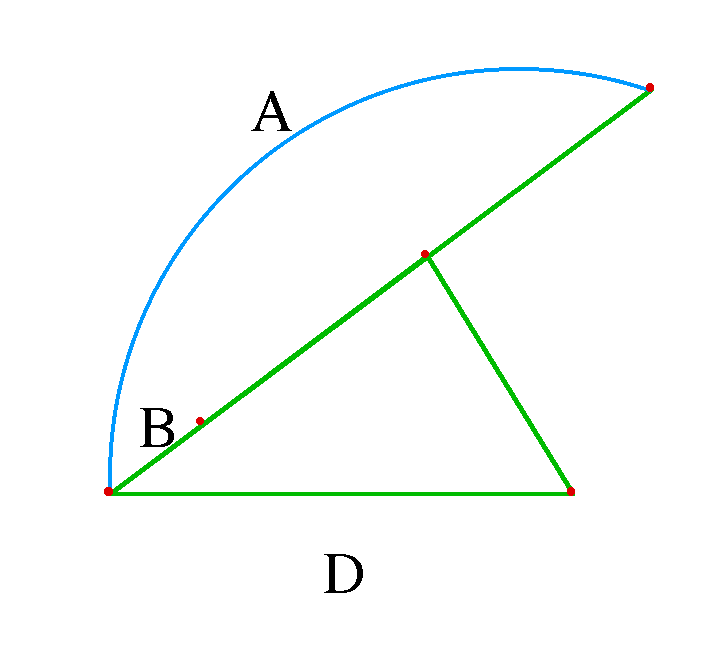
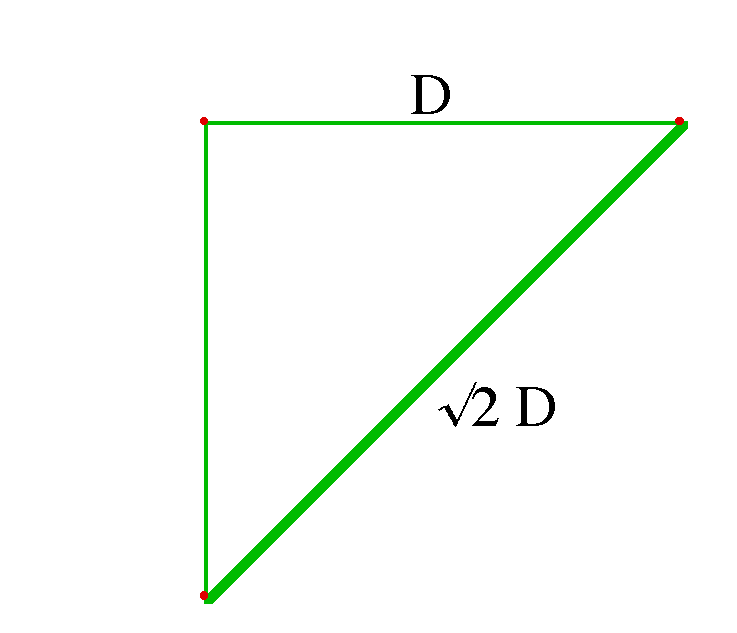
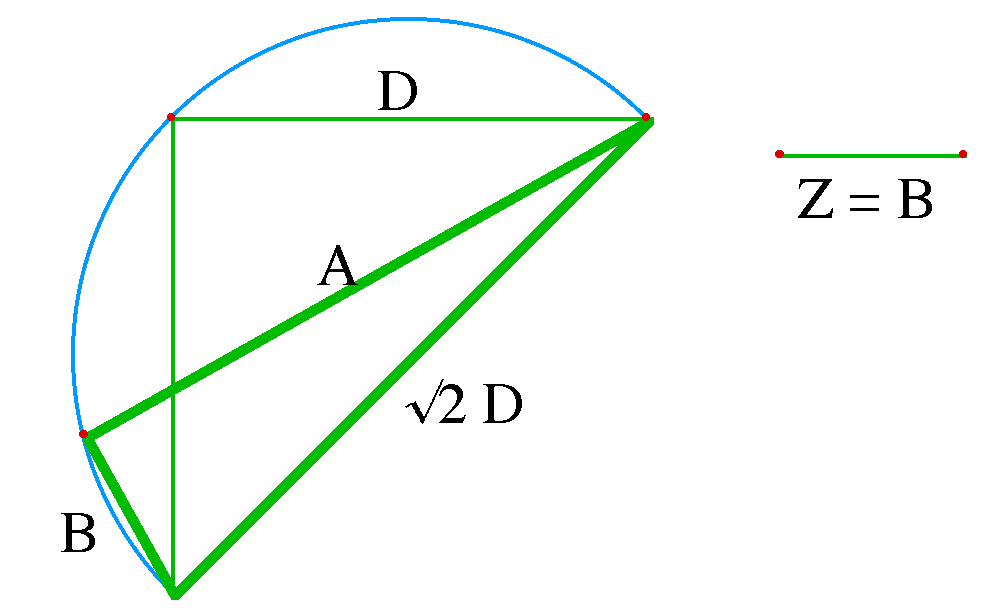
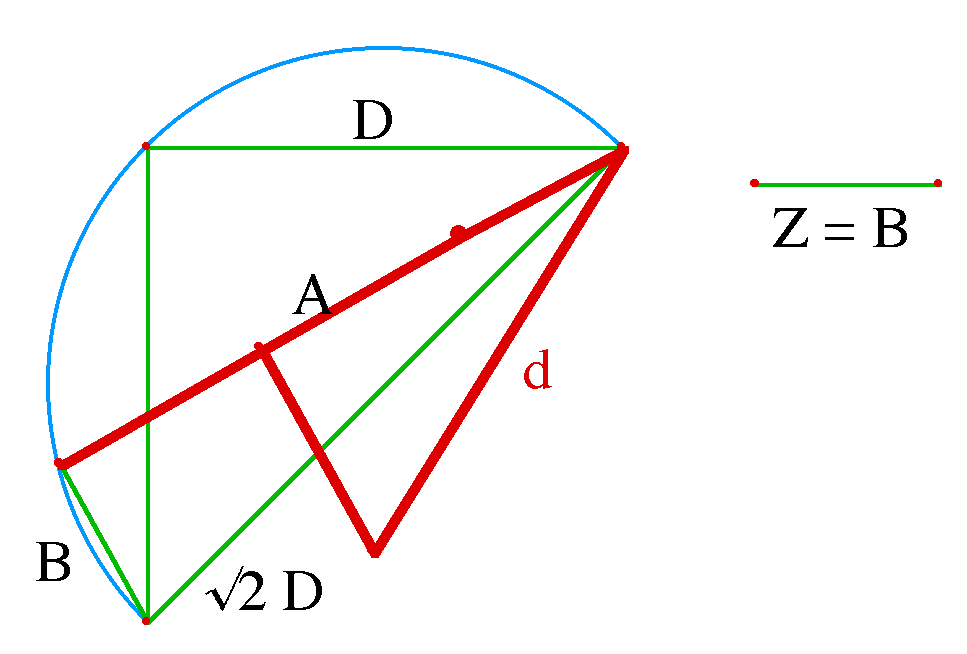
    Étant donné la base d’un triangle, sous-tendant l’angle droit, et la différence des cathètes. Trouver le triangle.

Résolution
Soit cela fait, avec D, la base et B la différence des cathètes.

A +B = 2 (grande cathète)
A - B = 2(petite cathète)
Or
la somme des carrés des cathètes = D2,
donc A2 + B2 = 2D2
ou A2 = 2D2 - B2 (le porisme)

 

 

 

 

(Suite de la composition)

Par construction, on a
A2 = 2D2 - B2,
donc, par l’équivalence des propositions de la résolution,
A+B = 2 (grande cathète)
A-B = 2 (petite cathète)
et, par calcul,
d2 = la somme des carrés des cathètes = ((A+B)/2)2 + ((A-B)/2)2
= (A2 + B2)/2 = (Racine2 D)2
= D2.

On a donc d2 = D2, d’où d = D.

Composition
[Construction : reproduire le porisme]

A satisfait le porisme.
Connaissant la somme A et la différence B, construire le triangle.

Le triangle d’hypoténuse d satisfait le porisme. Reste à montrer que d = D
Cela se fait par l’inverse de la résolution.
(suite colonne de gauche)

 

8. Albert Girard (1595-1632) Popularisation de la théorie des équations

    1629 : Invention nouvelle en l'algèbre

    Théorème fondamental de l'algèbre

    Exposants fractionnaires

    Accepte les solutions complexes (dites impossibles), mais aussi les solutions négatives, interprétant ces dernières géométriquement.

    Énonce clairement la relation entre les racines d'une équation polynomiale et les coefficients du polynôme.
    (Première apparition des fonctions symétriques des coefficients)

    1626 : introduit la notation sin, cos, tan en trigonométrie.

       

      9. Le retour à la géométrie :
      René Descartes       (1596-1650) et la « géométrie analytique »

    Extraits de La Géométrie (1 Mo)

     

    Activité 1: Comparez l'approche géométrique de Descartes pour résoudre l'équation z^2 = az - bb ( p. 303 de La Géométrie de Descartes) à celle d'al-Khwarizmi pour montrer la justesse de la résolution de la x^2 + 21 = 10x (p.70 du recueil)

    Activité 2 : Comparez l'approche de Viète et celle de Descartes.

Haut de la page