MAT 6221

Bas de la page

Trigonométrie (2)

Les tables d'Hipparque
et de Ptolémée

Les tables de cordes

Cette page s'inpire de Victor Katz, History of Mathematics, An introduction, 2ième édition, Addison-Wesley, 1998, 137 à 152.

Les tables d'Hipparque (190-120 av. notre ère)

• Hipparque utilise pour la première fois, semble-t-il, les degrés (360° pour un cercle complet)

• Les outils d'Hipparque :
  • La corde ( notée crd(a) [crd(a) = 2Rsin(a/2)] )
  • L'uniformisation des unités de mesures : pour l'angle et le rayon.

    Choix d'une unité telle que le rayon mesure 3438 = 57;18 telles unités , de sorte qu'un arc d'une minute a la même longueur qu'une unité sur le diamètre du cercle.

• Le calcul des tables (reconstruction à partir de l'Almageste de Ptolémée)
  • Les angles dont on connait les cordes
    • 60° : crd(60°) = le rayon = R = 3438
    • 90° : crd(90°) = Racine de 2 = 81;2
  • Les identités nécessaires (R = 3438)
    • crd(180° - a) = Racine[(2R)² - crd²(a)] [= 2Rcos(a/2)] ¶ (preuve)
    • crd²(a/2) = R(2R - crd(180° - a)) ¶ (preuve)
      • [sin²(b/2) = (1-cos(b))/2 (traduction directe)]
    • Utilisant l'identité du demi-angle, on ajoute à la liste des cordes : 45°, 30°, 22° 1/2, 15°; 7° 1/2.
    • Utilisant l'identité du supplément d'un angle, on ajoute à la liste :
      172° 1/2, 165° (puis 82; 1/2), 157° 1/2, 150° (puis 75° et 37° 1/2, et de 75° on a 105° et 52° 1/2), 142° 1/2, 135° (puis 67° 1/2), 120°.
    • On a ainsi les cordes des angles de 7° 1/2 à 180°, par sauts de 7° 1/2.

Les tables de Ptolémée (100-178)

• L'Almagest : Titre original Composition mathématique (Matematike syntaxe) qu'on a pris l'habitude d'appeler le Magesti syntaxis (grande composition). Les arabes ont « arabisé » ce titre commun en al-Magesti. Ce titre arabisé a été par la suite latinisé en Almageste. C'est resté le livre de référence jusqu'à copernic au XVIe siècle.
• Table des cordes, de 1/2° à 180°, par sauts de 1/2°.
  • Choix du rayon : 60 au lieu du 57; 18 d'Hipparque.
  • Base du calcul : crd(36°), qui correspond au côté du décagone inscrit dans le cercle
    • Il réussit à calculer ce côté en utilisatn deux propositions des Éléments d'Euclide (II-6 et XIII-9)
      crd(36°) = 37;4,55
    • Or, par la proposition XIII-10 des Éléments (Si un pentagone équilatéral est inscrit dans un cercle, le carré sur le côté du pentagone est égal aux carrés sur le côté de l'exagone et sur celui du décagone inscrits dans el même cercle.), on a crd^2(72°) = crd^2(60°) + crd^2(36°). Donc, on peut calculer crd(72°). Crd(72°) = 70;32,3.
    • On connaît donc les cordes de 36°, 60°, 72°, 90° et leurs supppléments (par l'une des identités d'Hipparque).
  • 2Rcrd(a-b) = crd(180°-b)crd(a) - crd(180°-a)crd(b)
    • [sin(a-b) = cos(y)sin(x) - cos(x) - cos(x)sin(y) (traduction directe, R = 1)]
    • [cos(x+y) = cos(x)cos(y) - sin(x)sin(y) (posant 2a = 180°-2x, b = 2y, R = 1)]
    • Pour démontrer cette identité:
      • Théorème de Ptolémée : Si un quadrilatère est inscrit dans un cercle, le rectangle construit sur les diagonales du quadrilatère est égal aux (à la somme des) rectangles sur les côtés opposés du quadrilatère.(Si ABCD est le quadrilatère, on a AC•BD = AD•BC + AB•DC).
      • L'identité découle de l'application du théorème dans le cas de figure suivant

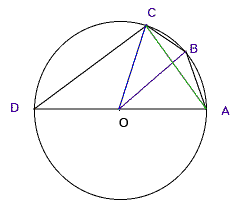      l'angle a est l'angle COA
      l'angle b est l'angle BOA.

  • En appliquant l'identité à la différence des angles de 72° et 60°, on obtient:

    crd(72°-60°) = crd(12°).
    Puis, par divisions par deux successives, on obtient finalement crd(3/4°).
    On pourrait donc avoir une table par sauts de 3/4°.

  • Mais Ptolémée veut, semble-t-il, une table par sauts de 1/2°.
    • Lemme : si a<b alors crd(b)/crd(a) < b/a.[Preuve]
    • De ce lemme on tire que
      (2/3)crd(3/2°) < crd(1°) et crd(1°) < (4/3)crd(3/4°).
    • Or, par le calcul précédant, on a (2/3)crd(3/2) = 1;2,50 et (4/3)crd(3/4) = 1;2,50 (à la deuxième position près, ce qui est la précision habituelle).
    • Donc, crd(1°) = 1;2,50, d'où crd(1/2°) = 0;31,25.
  • Ptolémée peut donc maintenant calculer tout sa table de 1/2° à 180°, par sauts de 1/2°.

Exemples de problèmes astronomiques

• Problème 1 : 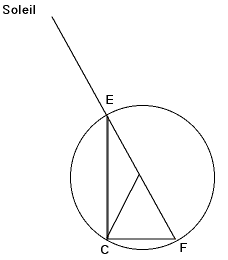Calculer la longueur CF de l'ombre d'un bâton CE, de longugeur 60, à midi à Rhodes (latitude 36°), lors de l'équinoxe du printemps.

  • À l'équinoxe du printemps, à midi, le soleil forme avec le zénith un angle égal à la latitutde.

  Donc l'angle en E est 36° et la corde CF correspond à un angle de 72°.

  • Si le cercle était un cercle de rayon 60, alors on pourrait trouver par les tables la corde CF. Mais ce n'est pas le cas. Tout ce que l'on sait c'est que le baton CE mesure 60. Or la corde CE correspond à une corde de l'angle 180°-72°. Dans le cercle de rayon 60, les tables nous donne que crd(180°-72°) = 97;4;54. Par ailleurs, dans le cercle ici, on a 60 comme longueur. Donc, on peut calculer CF. CF = crd(72°) x(60/crd(180°-72°) = 43;36.

• Problème 2 : Calculer de déplacement du centre de l'équant de l'orbitre du soleil.

  • Les données :
    - La vitesse angulaire constante v de rotation de l'équant est 360°/(365 1/4 j.) = 0° 59'8"/j.
    - Le temps pour le soleil d'aller de l'équinoxe du printemps au solstice d'été : 94 1/2 jours.
    - Le temps pour le soleil d'aller du solstice d'été à l,équinoxe d'automne : 92 1/2 jours.
  • Il faut résoudre le triangle TLD dans la figure ci-contre.
    • Calcul des angles a et b
      on a, du printemps à l'été, 90° + a + b = 94j.1/2xv
      et, de l'été à l'automne, 90 - b + a = 92j.1/2 x v, ou v = 0° 59' 8"/j.
      On a donc a = 2°10' et b = 0° 59'.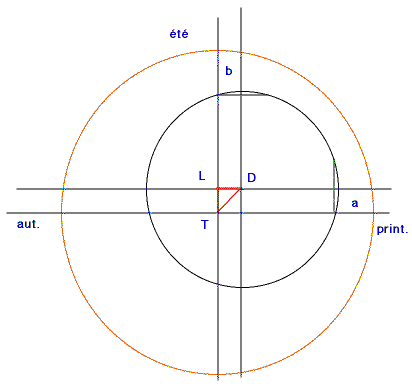
    • Calcul des demi-cordes, ce qui me donnera TL et LD, et donc aussi TD.

    TL = (1/2)crd(2a) = 2;16

    LD = (1/2)crd(2b) = 1;2

    TD = 2;29,30

    L'orbitre du soleil est de rayon 60 dans ces calculs, ce qui permet d'utiliser les tables.

    • Résolution du triangle TLD (trouver les angles). Cherchons l'angle en T.

    Inscrivons le triangle TLD dans un cercle centré sur le centre de l'hypothénuse.

    

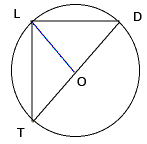
    Ce cercle a un diamètre de 2;29,30. La corde de l'angle LOD est de longueur 1;2. Pour trouver ce dernier angle, il suffit de comparer à un cercle de rayon 60 (diamètre 120). Dans ce cercle, la corde correspondant à l'angle LOD sera de longueur 1;2 x 120 / 2;29,30 = 49;46.
    En utilisant à l'enver la table des cordes, on a que l'angle LOD est 49°, d'où l'angle en T est 24° 30'.

    • Remarques : Notez que dans le calcul, ce sont les demi-cordes qui sont importantes et non les cordes elles-mêmes.
    • Remarques : On utilise ici l'idée d'une fonction inverse (en fait corde inverse).

     

• Problème 3 Résoudre le triangle scalène KLM sachant que l'angle BKL = c > 90° et que KL = B et MK = A sont donnés.

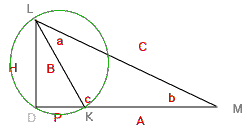
  • Prolongeons KM à D pour obtenir un triangle rectangle DLM.
  • Dans le triangle DLK, on a (R = 60)
    P = crd(2(c - 90°)) x b/2R
    H = crd(2(180°-c)) x b/2R
  • Dans le triangle DLM,
    C² = H² + (P+A)² = H² +P² + 2AP + A²
    = B² + A² + 2AP = A² + B² + 2Acrd(2(c - 90°)) x B/2R = A² + B² + 2A2Rsin(c-90°) x B/2R = A² + B² - 2ABcos(c)
    C'est la loi du cosinus (qui est une extension du théorème de Pythagore)

  On a donc trouver C.

  • Pour trouver l'angle b,
    il suffit de remarquer que crd(2b) = 2R(H/C) puis d'utiliser les tables de cordes pour détermienr la valeur de l'angle b.

  L'égalité utilisée correspond à sin(b) = (H/C) = (Bsin(c))/C, ce qui est la loi des sinus.

La trigonométrie en Inde

• Époques concernées

  La période de Kushan (1er siècle de notre ère) et des Gupta (4-6e siècles).

• Influence en ce qui a trait à la trigonométrie et l'astronomie : principalement Hipparque.

• Premier ouvrage : Paitamahasiddhanta (5e siècle)

  • On y retrouve une table de demis-cordes plutôt qu'une table de cordes (Voir problème 2 de Ptolémée)
  • Table basée sur un cercle de rayon 3438, comme Hipparque.

 

• Le Aryabhatiya d'Aryabhata (466-550)

• Écritàen 499, alros que l'auteur a 33 ans.
• Il écrit souvent simplenent Jya ou Jiva au lieu de jya-ardha (corde-demi)
• 33 énoncés mathématiques sur 123 dans le livre.
• Calcul de la table, par sauts de 3°45'.

 

Stenza I-10 Les vingt-quatre demi-arc [différences] calculées en minutes d'arc sont 225, 224, 222, 219, 215, 210, 205, 199, 191, 183, 174, 164, 154, 143, 131, 119, 106, 93, 79, 65, 51, 37, 22, 7

Stenza II-12 De combien la deuxième [différence des ] sinus est moins que le premier et par le quotient obtenu en divisant la somme des [différences] des sinus précédentes par le premier sinus, par la somme de ces deux quantités la [différence] des sinus suivants sont moins que le premier sinus.

Formule sous-jacente à ce dernier énoncé :

s_n = s_n-1 + (s₁ - (s₁ + ... + s_n-1)/s₁)

On peut penser que les tables ont été calculées un peu comme celle d'Hipparque et que cette méthode en a été déduite. On peut retrouver ce genre de formule en remarquant que la seconde différence est proportionnelle à la valeur du sinus (coefficient de proportionnalité : 225, le s₁. En effet, on a alors d²s_i = s_i/s₁. Or ds_n-1 = s₁ - d²s₁ - d²s2 - ... - d²s_n-1, en remarquant que ds₁ = s_1.

• Remarquez l'approche purement numérique
• Le sinus est vu ici, et jusqu'au début XVIIe siècle, d'abord comme un segment dans un cercle.

 

• Origine du mot sinus

  Aryabhata écrit souvent simplenent Jya ou Jiva au lieu de jya-ardha (corde-demi). Losque les Arabes traduiront les textes indiens, il utiliseront à nouveau le terme indien courant Jiva, qui ne veut par ailleurs rien dire en arabe. Toutefois, en arabe, on n'écrit souvent que les consonnes. Dès lors, le mot Jiva va s,écrire Jb et sera lu plutôt comme Jaïb, qui signifie poitrine ou col. Lors de la traduction en latin des livres arabes, les Européens emploieront le mot sinus qui veut précisément dire poitrine, col, ou baie. On rencontre le mot Sinus sur les cartes géographiques de la Renaissance et du XVIIe siècle pour les baies (Sinus Mexicanus par exemple sur des globes terrestres anciens du Musée Stewart de l'Ile St-Hélène)

• Tables de sinus et cosinus (demi-corde perpendiculaire)

  • Par Varahamihira (6e siècle)
  • Dans le Surya-siddhanta (7e siècle)
    • Indice de l'utilisation de la sécante (1/ccos) et de la tangente (sin/cos) dans l'étude des ombres.

• Les tables ne deviennent pas plus précises jusqu'au 12e siècle, donc besoin d'approximations

• L'importance des talbes de sinus dans l'histoire de la numération indienne

  (B.L. van der Waerden, Science Awakening, New York : Oxford Un. Press, 1961, pp. 53-58.)

  L'invention de la numération positionnelle indienne date probablement de vers 600. D'abord utilisée par les astronomes puis, après de nombeuses années, par les gens ordinaires.

  Les nombres poétiques : la mémorisation des tables de sinus.

  Vers 500, pour apprendre les tables de sinus, les astronomes associaient à chaque chiffre un mot qui le rappelait (ex. 1 : lune, bouche; 2: ailes, oreilles, yeux; 0: trou; etc.) de façon à transformer les tables en poèmes rimés. On rencontre cela dans le Surya-siddhanta (7e siècle) mentionné ci-dessus.

  Aryabhata avait développé un système de syllables qui exprimait à la fois les chiffres et l'ordre de grandeur de ce dernier (ex. ca voulait dire 6 unités (le a indiquant les unités ou les dizaines, le c signifiant 6), gi signifie 3 centaines (g: 3, i: centaines) etc.)
  ainsi cayagiyinusuchlr signifie 63335775 (du plus petit au plus grand de gauche à droite), pour nous : 57753336.

  Son disciple Bhaskara simplifie en enlevant les lettres pour les ordres de grandeurs. Il utilise un zéro. C'est un système positionnel.

• Méthodes d'approximation

• Brahmagupta (598-670), vers 650
  • Pour trouver le sinus d'un angle x, on détermine d'abord la valeur d'un angle x_i inférieur à x, qui est dans la table et le plus proche de x. Si D_{i est la ième différence (voir la Stenza I-10 plus haut) et si on note h comme étant les sauts de la table (3° 45'), Brahmagupta utilise la règle suivante :}

  sin(x) = sin(x_i +e) = sin(x_i) + (e/2h)(D_i + D_i+1) + (e²/2h²)(D_i - D_i+1).

  • Cette règle est donnée sans preuve.
  • Appliquée à x = 20° (e = 1° 1/4, x_i = 18°3/4, donc i = 5, D₅ = 215° et D₆ = 210°) on obtient sin(20°) = 1176. (En réalité 1175,87)

   

• Bhaskara (600-680 ??)
  • Sa règle est la suivante :

  Rsin(x) = (4Rx(180°-x))/(40 500 - x(180° - x))

  • Si x = 20°, Rsin(20°) = 1180 alors que le calcul plus exact donne 1179,80.
  • D'où vient cette règle ? (Hypothèse)
    • La fonction quadratiquee P(x) = Rx(180°-x)/8100 a les même valeurs que Rsin(x) pour x = 0°, 90° et 180°.
    • Ajustons-là pour que ce soit le cas pour 30° aussi.

    Rsin(30°) = R/2 alors que P(30°) = (5/9)R.
    Peut-être ont-ils eu l'idée de coincer le sinus entre P(x) et P(x)sin(x), car alors, à x = 30°, on a

    (P(x) - Rsin(x))/(Rsin(x) - P(x)sin9x)) = 1/4

    d'où on tire que Rsin(x) = 4P(x)/5-(P(x)/R) qui est de fait la règle de Bhaskara.

• Ces règles et leur utilisation plutôt que la recherche de tables plus précises, montre l'importance de la tradition dans l'usage des modes de calculs.
• Cela me fait aussi penser à Ramanujan (1887-1920), le génial calculateur ami de Hardy.
• Illustre aussi ce qui se passe lorsqu'il n'y a pas de recherche systématique de démonstrations.

La trigonométrie en Chine

• Liu Hui (3e siècle)

  • Manuel mathématiques sur les îles en mer.(9 problème d'arpentage)
  • Premier problème à propos d'une île, sa distance et la hauteur du sommet.
  • Quatrième problème : la profondeur et la distance d'un point dans une vallée. (Présence implicite de la tangente)

   

• Chutan Hsita (718) Neuf planètes (Ouvrage sur les éclipses)

  • Table de sinus par sauts de 3°45'. Influence indienne sans doute, car des bouddhistes indiens sont en Chine et amène avec eux les connaissances indiennes.

 

• Yi Xing (683-727)

• 724 : étude par l'empire des ombres d'un gnomon de 8', entre le 29° et 52° de latitude, le long d'un méridien (114° est)
• Table d'ombres de 1°à 79° d'angle zénithal. s(a) =8tan(a) = 8 (sin(a)/sin(90-a) (première table des tangentes, par les tables de sinus)

Haut de la page