
MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Trigonométrie (3)
La trigonométrie
après les Grecs
La trigonométrie après les Grecs
La trigonométrie après les Grecs
-
La mouvance numérique : L'Inde
-
La corde est délaissée pour être remplacée par le sinus et origine du mot sinus
-
Première table de cosinus, aussi peut-être tangente et sécante.
-
L'approximation plutôt qu'une plus grande précision des tables.
-
-
Détails sur l'Inde et la Chine :
-
Époques concernées
La période de Kushan (1er siècle de notre ère) et des Gupta (4-6e siècles).
-
Influence en ce qui a trait à la trigonométrie et l'astronomie : principalement Hipparque.
-
Premier ouvrage : Paitamahasiddhanta (5e siècle)
- On y retrouve une table de demis-cordes plutôt qu'une table de cordes (Voir problème 2 de Ptolémée)
- Table basée sur un cercle de rayon
3438, comme Hipparque.
-
Le Aryabhatiya d'Aryabhata (466-550)
-
- Écrit en 499, alors que l'auteur a 33 ans.
- Il écrit souvent simplement Jya ou Jiva au lieu de jya-ardha (corde-demi)
- 33 énoncés mathématiques sur 123 dans le livre.
- Calcul de la table, par sauts de 3°45'
(la moitié du saut de 7°1/2 d'Hipparque)
Stenza I-10 Les vingt-quatre demi-arc [différences] calculées en minutes d'arc sont 225, 224, 222, 219, 215, 210, 205, 199, 191, 183, 174, 164, 154, 143, 131, 119, 106, 93, 79, 65, 51, 37, 22, 7
Stenza II-12 De combien la deuxième [différence des ] sinus est moins que le premier et par le quotient obtenu en divisant la somme des [différences] des sinus précédentes par le premier sinus, par la somme de ces deux quantités la [différence] des sinus suivants sont moins que le premier sinus.
Formule sous-jacente à ce dernier énoncé :
sn = sn-1 + (s1 - (s1 + ... + sn-1)/s1)
On peut penser que les tables ont été calculées un peu comme celle d'Hipparque et que cette méthode en a été déduite. On peut retrouver ce genre de formule en remarquant que la seconde différence est proportionnelle à la valeur du sinus (coefficient de proportionnalité : 225, le s1. En effet, on a alors d2si = si/s1. Or dsn-1 = s1 - d2s1 - d2s2 - ... - d2sn-1, en remarquant que ds1 = s1.
- Remarquez l'approche purement numérique
- Le sinus est vu ici, et jusqu'au début XVIIe siècle, d'abord comme un segment dans un cercle.
-
Origine du mot sinus
Aryabhata écrit souvent simplement Jya ou Jiva au lieu de jya-ardha (corde-demi). Lorsque les Arabes traduiront les textes indiens, il utiliseront à nouveau le terme indien courant Jiva, qui ne veut par ailleurs rien dire en arabe. Toutefois, en arabe, on n'écrit souvent que les consonnes. Dès lors, le mot Jiva va s,écrire Jb et sera lu plutôt comme Jaïb, qui signifie poitrine ou col. Lors de la traduction en latin des livres arabes, les Européens emploieront le mot sinus qui veut précisément dire poitrine, col, ou baie. On rencontre le mot Sinus sur les cartes géographiques de la Renaissance et du XVIIe siècle pour les baies (Sinus Mexicanus par exemple sur des globes terrestres anciens du Musée Stewart de l'Ile St-Hélène)
-
Tables de sinus et cosinus (demi-corde perpendiculaire)
- Par Varahamihira (6e siècle)
- Dans le Surya-siddhanta (7e
siècle)
- Indice de l'utilisation de la sécante (1/cos) et de la tangente (sin/cos) dans l'étude des ombres.
- Les tables ne deviennent pas plus précises jusqu'au 12e siècle, donc besoin d'approximations
-
L'importance des tables de sinus dans l'histoire de la numération indienne
(B.L. van der Waerden, Science Awakening, New York : Oxford Un. Press, 1961, pp. 53-58.)
L'invention de la numération positionnelle indienne date probablement de vers 600. D'abord utilisée par les astronomes puis, après de nombreuses années, par les gens ordinaires.
Les nombres poétiques : la mémorisation des tables de sinus.
Vers 500, pour apprendre les tables de sinus, les astronomes associaient à chaque chiffre un mot qui le rappelait (ex. 1 : lune, bouche; 2: ailes, oreilles, yeux; 0: trou; etc.) de façon à transformer les tables en poèmes rimés. On rencontre cela dans le Surya-siddhanta (7e siècle) mentionné ci-dessus.
Aryabhata avait développé un système de syllabes qui exprimait à la fois les chiffres et l'ordre de grandeur de ce dernier (ex. ca voulait dire 6 unités (le a indiquant les unités ou les dizaines, le c signifiant 6), gi signifie 3 centaines (g: 3, i: centaines) etc.)
ainsi cayagiyinusuchlr signifie 63335775 (du plus petit au plus grand de gauche à droite), pour nous : 57753336.Son disciple Bhaskara simplifie en enlevant les lettres pour les ordres de grandeurs. Il utilise un zéro. C'est un système positionnel.
Méthodes d'approximation
- Brahmagupta (598-670), vers 650
- Pour trouver le sinus d'un angle x, on détermine d'abord la valeur d'un angle xi inférieur à x, qui est dans la table et le plus proche de x. Si Di est la ième différence (voir la Stenza I-10 plus haut) et si on note h comme étant les sauts de la table (3° 45'), Brahmagupta utilise la règle suivante :
sin(x) = sin(xi +e) = sin(xi) + (e/2h)(Di + Di+1) + (e2/2h2)(Di - Di+1).
- Cette règle est donnée sans preuve.
- Appliquée à x = 20° (e = 1° 1/4, xi = 18°3/4, donc i = 5, D5 = 215° et D6 = 210°) on obtient sin(20°) = 1176. (En réalité 1175,87)
- Bhaskara (600-680 ??)
- Sa règle est la suivante :
Rsin(x) = (4Rx(180°-x))/(40 500 - x(180° - x))
- Si x = 20°, Rsin(20°) = 1180 alors que le calcul plus exact donne 1179,80.
- D'où vient cette règle ? (Hypothèse)
- La fonction quadratique P(x) = Rx(180°-x)/8100 a les même valeurs que Rsin(x) pour x = 0°, 90° et 180°.
- Ajustons-la pour que ce soit le cas pour 30° aussi.
Rsin(30°) = R/2 alors que P(30°) = (5/9)R.
Peut-être ont-ils eu l'idée de coincer le sinus entre P(x) et P(x)sin(x), car alors, à x = 30°, on a(P(x) - Rsin(x))/(Rsin(x) - P(x)sin9x)) = 1/4
d'où on tire que Rsin(x) = 4P(x)/5-(P(x)/R) qui est de fait la règle de Bhaskara.
- Ces règles et leur utilisation plutôt que la recherche de tables plus précises, montre l'importance de la tradition dans l'usage des modes de calculs.
- Cela me fait aussi penser à Ramanujan (1887-1920), le génial calculateur ami de Hardy.
- Illustre aussi ce qui se passe lorsqu'il n'y a pas de recherche systématique de démonstrations.
La trigonométrie en Chine
-
Liu Hui (3e siècle)
- Manuel mathématiques sur les îles en mer.(9 problème d'arpentage)
- Premier problème à propos d'une île, sa distance et la hauteur du sommet.
- Quatrième problème : la profondeur et la distance d'un point dans une vallée. (Présence implicite de la tangente)
-
Chutan Hsita (718) Neuf planètes (Ouvrage sur les éclipses)
- Table de sinus par sauts de 3°45'. Influence indienne sans doute, car des bouddhistes indiens sont en Chine et amène avec eux les connaissances indiennes.
-
Yi Xing (683-727)
- 724 : étude par l'empire des ombres d'un gnomon de 8', entre le 29° et 52° de latitude, le long d'un méridien (114° est)
- Table d'ombres de 1°à 79° d'angle zénithal. s(a) =8tan(a) = 8 (sin(a)/sin(90-a) (première table des tangentes, par les tables de sinus)
-
La mouvance géométrico-numérique : les Arabes
- Source religieuse de l'intérêt pour les
calculs trigonométriques
- La qibla (orientation vers La Mecque)
- La détermination de l'heure des cinq prières quotidiennes
- Définition de toutes les « fonctions
»trigonométriques
- cosinus : al-Battani (v. 855-929) utilise le complément à 90° du sinus d'un angle de moins de 90°. Pour les angles plus grand, il utilise le versinus(a) = R + Rsin(a-90°). Remarquons que cela remplace nos négatifs dans ce cas.
- Les quatre autres « fonctions »
Chez al-Hasib (v. 770-870) et surtout al-Biruni (973--1055), ces fonctions sont définies en termes de l'ombre d'un bâton d'une longueur donnée :
ombre directe (cotangente) GE
hypoténuse de l'ombre directe (cosécante) BE
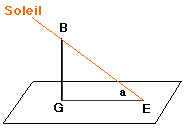
ombre renversée (tangente) GE
hypoténuse de l'ombre renversée (sécante) BE
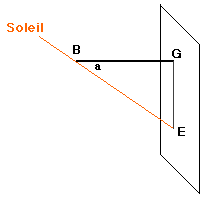
À partir de là on a aussi directement les formules reliant ces fonctions:
cot2(a) + 1 = csc2(a)
tan2(a) + 1 = sec2(a)
tan(a) = sin(a) /cos(a). Notez que c'est une identité ici et non une définition. - Vers l'utilisation dans la mesure :
Jal-Qabisi (10e siècle)
Calcul de la hauteur à partir de deux positions.x = y sin(90°-a)/sin(a)
y (à vous de le calculer)
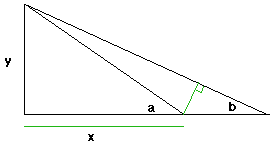
- Source religieuse de l'intérêt pour les
calculs trigonométriques
- Précision accrue des tables : al-Kashi (né
429)
- calcul à quatre positions sexagésimales
en remarquant que sin(1°) satisfait l'équation
3x + 4x3 = sin(3°). il trouve que 60sin(1°) = 3;8, 24, 33, 59, 34, 28, 15.
- calcul à quatre positions sexagésimales
en remarquant que sin(1°) satisfait l'équation
- Amélioration de la trigonométrie sphérique car nécessaire pour résoudre la qibla et le problème des prières quotidiennes.
-
Vers la trigonométrie du Triangle : l'Europe du Moyen Âge et de la Renaissance
- Remarque : première traduction de
l'Alamageste de Ptolémée
 :
1175, puis des livres arabes.
:
1175, puis des livres arabes. - Premières manifestations de la mesure :
les secteurs de cercle
- Abraham bar Hiyya (mort 1136)
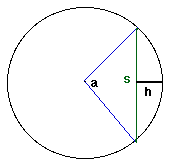
Table d'arcs de corde (arcsin) : R = 14 (pour C = 88 avec pi= 22/7) pour pouvoir mesurer des secteurs de cercle connaissant la longueur de la corde s et la distance maximale h de la corde à l'arc, selon la méthode suivante :
- diamètre = d = s2/4h + h
- calculer s x 28/diamètre, pour pouvoir utiliser la table
- utiliser la table pour trouver la longueur de l'arc
- arc trouvé x d/28, pour revenir dans notre cercle
- le secteur a pour aire (d x arc)/4. - Leonard de Pise (Fibonacci) (1175-1240)
Table de corde dans son Practica Geometriae (1220), R = 21 (C = 66)
- Abraham bar Hiyya (mort 1136)
- Deuxième manifestation de la mesure : les
rapports

Hugues de St-Vicor (1096-1141)
Introduction de l'alidade sur l'astrolabe (illustration provenant de Oxford museum of Science:
http://www.mhs.ox.ac.uk/).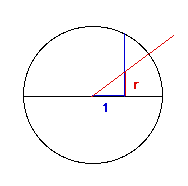
La mesure r nous donne le rapport de la hauteur de l'objet visé à la distance de cet objet.
Dès lors, pour calculer la distance d'un objet à partir de deux mesure avec l'astrolabe, il suffit d'utiliser la règle suivante
x = d/((r1/r2)-1)
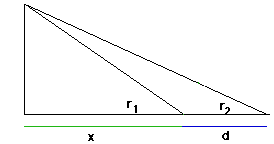
- L'héritage gréco-arabe au Moyen Âge
- Richard de Wallingford (1291-1336), un moine anglais
Reprend Ptolémée, mais à la Euclide, avec un intérêt pour les rapport et l'utilisation du sinus surtout, et non seulement la corde.
- Levi ben Gerson (1288-1344) un juif français
Dans son traité de philosophie Sefer Milhanot Adonai (Les guerres du Seigneur), il systématise la résolution des triangles plans et énonce clairement les lois du sinus et du cosinus. Tout cela pour un usage en astronomie.
- Les grands explorateurs : importance accrue des calculs
Besoin de déterminer la latitude et la longitude d'un bateau. Déterminer la longitude est particulièrement difficile. La latitude est déterminé par l'élévation du pôle (étoile polaire) au-dessus de l'horizon.
- La naissance de la trigonométrie du
triangle
- Regiomontanus (Johannes Muller de Kömigsberg (1436-1476) )
De triangulis omnimudis (1464), un livre très influent.
- Notion de grandeur et de rapport
- Table du sinus, R = 60 000
- Distingue clairement la trigonométrie dans un triangle plan et la trigonométrie sphérique.
- Utilisation de l'algèbre dans quelques problèmes.
- Par la suite, tables où R = 60 x 10n ou R = 10n à cause de l'absence de fraction s décimales.
- Le passage au triangle rectangle
- Georg Joachim Rheticus (1514-1574) le disciple de Copernic.
Il introduit les noms sinus et cosinus et les voit dans un triangle rectangle d'hypoténuse donnée, très grande (donc pas vraiment encore rapport).
- Thomas Finck (1561-1656), introduit en 1583 les termes tangente et sécante, et complément de sinus, complément de tangente et complément de sécante.
- La trigonométrie acquiert son nom : B.
Pitiscus(1561-1613) Trigonometriae sive, de
dimnesione triangulis, Liber (1595)
- Calcul des hauteurs avec un
quadrant
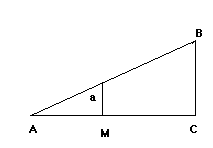 (Illustration : Oxford Museum of History of
Sciences : http://www.mhs.ox.ac.uk/).
(Illustration : Oxford Museum of History of
Sciences : http://www.mhs.ox.ac.uk/).
Deux méthodes
1) BC/AC = sin(90° -a)/sin(a)
2) Par la table des ombres (tangentes dans un triangle dont la base est 100 000)
AC/100 000 = BC/tan(90°-a)

- Calcul des hauteurs avec un
quadrant
- Remarque : première traduction de
l'Alamageste de Ptolémée
-
Vers de véritables fonctions trigonométriques
- 1614 : Napier et les logarithmes, pour le
calcul avec les sinus, pour chaque minute :
anglesin(a)log sin(a)log tan(a)log sin(90°-a)cos(a)90°-a34° 40'5688011564224236878721954370822475155°20'
- 1637 : Roberval trace, dans son étude de la cycloïde, la courbe d'équation y = a(1-cos(x/a)) et y = sin(x)
- 1657 Pascal, Traité du sinus du cercle, calcul l'aire sous la courbe rsin(x)
- 1668 James Gregory (1638-1675) développe la fonction arcsin (x) en une série. (Résultat connu en Inde en 1530)
- 1693 Leibniz caractrise le sinus par d2y/dx2 = -y.
- !730-1748 : Euler, le véritable inventeur des fonctions trigonométriques. Le cercle de rayon 1 devint la norme en trigonométrie.
- 1807 Fourier utilise les séries
trigonométriques pour représenter des fonctions.
- Au cours du siècle : définition d'ensembles, étude de l'intégrale comme une mesure de surface, notion générale de fonction.
- 1614 : Napier et les logarithmes, pour le
calcul avec les sinus, pour chaque minute :
-
Le radian :
- Première fois par James T. Thomson en 1873 dans un examen. Première publication vraiment publique en 1874, Alexander J. Ellis, Algebra Identified with Geometry.
- Le terme radian n'a pas été utilisétout de suite. Plutôt on employait radial, ou pi-measure, un circulaire.
- Le but de l'utilisation d'une nouvelle mesure : simplifier les calculs, spécialement en calcul différentiel et intégral des fonctions trigonométriques et pour les calcul de vitesses et d'accélération de mouvements curviligne. (Un exercice pour vous faire penser : calculer la dérivée de la fonction sinus défini pour un angle mesuré en degrés et non en radians. De même, calculer la limite du rapport de sin(x) /x, si x est en degrés.)
-
Quelques considérations didactiques sur l'histoire de la trigonométrie.
- Pour le sinus et le cosinus, passer d'abord par le triangle rectangle n'est pas nécessaire a priori. D'ailleurs, l'approche directement par le cercle enlève la difficulté de traiter du sinus de 90° ou de 0° par exemple.
- Le fait de commencer par la trigonométrie du triangle dans l'enseignement oblige, lorsque l'on passe à la trigonométrie du cercle, à étendre la nation de sinus, et des autres rapports trigonométriques, à des angles plus grands que 90°. Historiquement, ce qu'on a fait ce n'est pas d'étendre ces notions mais bien de restreindre au triangle ce que l'on faisait dans le cercle. Mathématiquement, c'est plus simple de restreindre que d'étendre.
- La notion de « fonction trigonométrique » a précédé celle de « rapport trigonométrique ». cela a été possible par l'usage des tables de valeurs.
- Ces tables ont aussi permis l'utilisation des « fonctions inverses ».
- La trigonométrie n'est pas nécessaire pour résoudre la très grande majorité des problèmes pratiques d'arpentage ou de mesure. On peut éviter la trigonométrie par l'emploi des similitudes.
- On peut travailler avec les fonctions
trigonométriques sans utiliser les radians.
- Hipparque : de l'arc au rayon
- Ptolémée : indépendance du rayon et de l'arc (R = 60 et arc mesuré en degrés (°))
- Euler : indépendance du rayon et de l'arc ((R = 1, arc en degrés)
- Radians : du rayon à l'arc. Mais sait-on ce qu'est un radian ?
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |