
MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Trigonométrie (4)
La trigonométrie après la Renaissance
De 1600 à 1900
De 1600 à 1900
-
Copernic (1473-1543)
- Il reste très près de Ptolémée : sans profiter du travail des Arabes ni même de celui de Regiomontanus : toujours les cordes et non le sinus. Mais R = 1000 000 et les tables donne la demi-corde du double de l'arc. N'utilise pas la loi du sinus, il se ramène toujours à des triangles rectangles.
-
Kepler (1571-1630)
Bibliographie :
Alexandre Koyré, La révolution astronomique, Copernic, Kepler, Borelli, Paris : Herman, 1961, chap. VIII et IX.
Kepler, Le musicien du ciel, Pour la Science, Les génies de la science, n° 8, août-novembre 2001, pp. pp. 44-51.
Victor Katz, History of Mathematics, p. 409-416.
Eric j. Aiton, How Kepler Discoverd the Elliptical Orbit, The Mathematical Gazette, vol. 59, December 1975, n° 410, pp. 250-260.Les première et deuxième lois de Kepler pour les orbites des corps célestes.
- Par les mesures de Tycho Brahé et les siennes, Kepler constate que l'orbite de la Terre et de Mars ont une excentricité e (distance entre le Soleil et le centre de l'orbite) supérieure à la marge d'erreur des mesures. Cette excentricité (e) existe donc vraiment. Il se rend aussi compte que la vitesse linéaire des planètes varie en fonction de la distance au Soleil, et que le minimum et le maximum se produisent à l'aphélie et au périhélie. Cela est en accord avec son principe que le force du soleil est inversement proportionnelle à la distance au soleil. À ces points, la vitesse est inversement proportionnelle à la distance au soleil.
- Il étend cette règle de vitesse inversement proportionnelle à tous les points de l'orbite (D'abord en divisant son cercle en 180 parties, puis en considérant une infinité de parties). Dans chacune de ces parties on a donc v = k/PS, où PS est la distance Terre-Soleil (ou planète-Soleil). donc, vitesse x PS = k. Supposant tout constant pour cette partie du cercle, et que cela prend un temps t, toujours le même pour parcourir une de ces parties (car la vitesse angulaire autour d'un certain point est constante), on a que vitesse x t x PS = k x t. Or vitesse x t = distance parcourue. De plus, vitesse x PS est proportionnel à l'aire du triangle très petit formé par le secteur d'orbite délimité par les positions extrêmes de la planète pour la partie d'orbite. Donc, dans le temps t nécessaire pour parcourir chacune de ces parties, l'air balayée par le rayon PS est la même; d'où la première loi : le rayon vecteur PS balaie des aires égales en des temps égaux. (1602). Cette loi (qui est en fait la première découverte par Kepler) lui servira par la suite pour déterminer l'orbite de Mars.
- Question : déterminer la position de la
planète à un instant donné. (Réponse dans le Astronomia
Nova, 1609)
- Il constate que 2 ensembles de trois points de l'orbite de mars déterminent des cercles égaux. Donc l'orbite ne peut être circulaire.
- De plus, si on prend la demi-distance entre l'aphélie et le périhélie comme le rayon d'un cercle, la deuxième loi ne se vérifie pas.
- Il essaie avec un déférent (à vitesse non constante) et un épicycle. Cela lui donne un oeuf. Pour vérifier sa deuxième loi, il approxime l'oeuf par une ellipse, car la mesure des aires d'une ellipse a été étudié par Archimède et les Grecs, alors que rien n'a été fait pour son « oeuf ». Mais le grand axe de l'ellipse est trop long par rapport au calcul. Il doute de sa seconde loi.
- À partir de 22 observations précises de mars, il voit que l'orbite s'approche d'une ellipse parfaite.
- Il remarque alors qu'à la mi-chemin
entre les absides, la distance AR entre l'orbite et le
cercle dans lequel l'orbite est inscrit est 0,00429 du
rayon et que cela est égal à (e2)/2.
Il fait alors le calcul suivant : CA/CR = 1,00430, ce qui est très prêt de 1,00429. - Lui
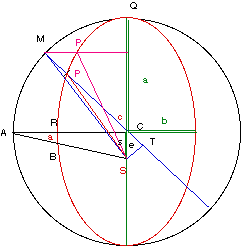 vient
alors à l'esprit que 1,00429 est la sécante de l'angle
a, à la mi-chemin entre les absides. Il tire de là que
SA/CA étant la sécante de a et que CA/CR étant égale à
peu près à SA/SB, on a SA/SB = SA/CA. Il généralise en
remarquant que CA est la projection de SA sur le rayon
du cercle et conjecture, en écrivant SP pour la distance
entre le soleil et la planète, qu'on a la proportion
vient
alors à l'esprit que 1,00429 est la sécante de l'angle
a, à la mi-chemin entre les absides. Il tire de là que
SA/CA étant la sécante de a et que CA/CR étant égale à
peu près à SA/SB, on a SA/SB = SA/CA. Il généralise en
remarquant que CA est la projection de SA sur le rayon
du cercle et conjecture, en écrivant SP pour la distance
entre le soleil et la planète, qu'on a la proportion
SM/SP = SM/MT.
D'où, SP = MT et donc SP = MC + ecos(c).
Reste à savoir où est véritablement la planète, puisque cette conjecture permet simplement de calculer la distance planéte-soleil à chaque instant et non la position exacte de la planète.
- Il choisit dans une première tentative
de prendre le point à distance MC + ecos(c) qui se
trouve sur le rayon MC.
Mais il constate que même si la courbe ainsi obtenue, qui n'est pas une ellipse, protège la distance par rapport à l'observation, elle ne protèges pas les angles. Il y a une erreur de 5' avec les observations. - Il revient au déférent et à l'épicycle, sans succès.
- Il reprend les calculs avec sa formule pour la distance au soleil, en gardant la distance SP = MC +ecos(c), mais il place le point sur la perpendiculaire abaissé sur le rayon entre les absides depuis le point M d'intersection de l'angle c avec le cercle circonscrit. Alors, reprenant les calculs en tenant compte de l'angle s, au Soleil, il montre que la courbe obtenue est une ellipse, qu'elle correspond aux observations et qu'elle satisfait sa deuxième loi.
On peut montrer qu'il s'agit bien d'une ellipse, si on pose a = 1 et b = 1-(e2)/2, et en considérant que le segment se terminant à P perpendiculaire au rayon des absides est toujours b fois celui se terminant à M, ce qui une propriété des ellipses :
Notant SP par R, on a R cos(s) = e + cos(c) et Rsin(s) = bsin(c). Calculant par là la valeur de R, en élevant les deux égalités au carré, on a R2 = e2 + 2ecos(c) + 1 - e2sin2(c) + (e4sin2(c))/4.
En négligeant le terme de degré 4, on obtient R = 1 + e2 cos(c). De plus l'excentricité de l'ellipse (la racine carré de la différence des carrés des axes) est 1 - b2 = e2, si le terme de degré 4 est ignoré. Depuis ce temps, l'excentricité est utilisée pour distinguer les différentes coniques.
-
Viète (1640-1603)
[François Viète, Oeuvres Mathématiques, Deuxième partie : Oeuvres géométriques, trigonométrie, suivie de la relation du calendrier véritablement grégorien, trad. par Jean Peyroux, Paris, 1992, p. 204.]
Vocabulaire :sinus total (le rayon de la table trigonométrique), sinus, sinus du restant à un droit (sinui reliqui è recto : cosinus pour nous), prosinus (tangente), transinus (sécante), prosinus du restant d'un droit (cotangente), transinus du restant d'un droit (cosécante).
- Exemple :
-
Napier (1550-1617) et les logarithmes
Étant donné les angles d'un triangle rectangle plan, les côtés sont donnés dans les parties de la Table.
En effet :
D'après la première série tabulaire :
La perpendiculaire sera faite semblable au sinus de l'angle aigu. La base, au sinus du restant à un droit. L'hypoténuse, au sinus total.Ou,
D'après la seconde série :
La perpendiculaire sera faite semblable au sinus total. La base, au prosinus de l'angle aigu. La base, au sinus total. L'hypoténuse, au transinus de l'angle aigu.
1614 : Napier et les logarithmes, pour le calcul avec les sinus, pour chaque minute, R = 10 000 000 :
Les calculs trigonométriques facilités par ce genre de table.
- Première utilisation systématiques des fractions décimales en mathématiques supérieures
- Règles de Napier : notation Nlog
- Nlog(R) = 0
- si a/b = c/d alors Nlog(a) - Nlog(b) = Nlog(c) - Nlog(d)
- d'où x/y = y/z ==> 2 Nlog(y) = Nlog(x) + Nlog(y)
- et x/y = z/w ==> Nlog(x) + Nlog(w) = Nlog(y) + Nlog(z)
- NB : on n'a pas Nlog(xy) = Nlog(x) + Nlog(y)
- Un exemple : Dans un triangle rectangle, si on connaît deux côtés, A et C, C étant l'hypoténuse, on peut trouver l'angle a opposé au côté A connu de l'angle droit :
sin(a)/R = A/C. Donc Nlog(sin(a)) = log(A) - log(C) + Nlog(R), où Nlog(R) = 0.- Un autre exemple : Dans un triangle quelconque, A et B, des côtés connus et a, l'angle opposé à A, connu. Résoudre par la loi des sinus. Les Nlog permettent de faire le calcul. Il y a deux solutions, l'une inférieure à 90°, l'autre, supérieure.
- Le Nlog de la fonction sécante s'obtient en changeant le signe de Nlogcos.
- 1637 : Roberval (1602-1675) trace, dans son étude de la cycloïde, la courbe d'équation y = a(1-cos(x/a)) et y = sin(x). (Voir le cours 10 pour le tracé de (1-cos(x)).)
- 1657 Pascal (1623-1662) , Traité du sinus du cercle, calcul l'aire sous la courbe rsin(x). On voit une relation entre le calcul de l'aire sous le sinus et le cosinus.
[ Pascal, Oeuvres complètes, Macmillan company, 1963. p. 157.
Fragment du Traité des sinus du quart de cercle In Geodefroy-Guillaume Leibniz, Oeuvre concernant le calcul infinitésimal, trad. Jean Peyroux, Paris : Blanchard, n.d., p. 123-127. UQAM QA302 L452]
- 1668 James Gregory (1638-1675) développe la fonction arcsin (x) en une série. Il fait de même pour arctan (Résultat connu en Inde en 1530).
- 1693 Leibniz
(1646-1716)
 caractérise le sinus par d2y/dx2 = -y.
caractérise le sinus par d2y/dx2 = -y.
[Katz, Victor, History of Mathematics, pp. 529-530.]
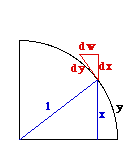
Dans le cadre de son étude sur la fonction sinus, Leibniz est amené à choisir une notation pour la dérivée seconde qui correspond à notre notation actuelle. Voici les calculs qui le mène à cette notation (Voir la figure)
Leibniz étudie la fonction sin(y) = x, où y est un arc du cercle de rayon 1.On a que le triangle différentiel (dx, dy, dw) est semblable au triangle dans le cercle [les côtés sont respectivement prenpendicuaires]. De cette similitude on a
dw/dx = x/Racine(1-x2), d'où dw = x dx/Racine(1-x2).
Or dx2 + dw2 = dy2, et donc dy2 - dx2 = dw2 = x dx2 / Racine(1-x2). En calculant et simplifiant, on obtient
dy2 = dx2 + x2dy2.
En considérant que dy est constant (le pas de la différentiation), il applique d, comme opérateur et obtient
d(dy2) = d(dx2 + x2dy2), soit 0 = d(dx2 + x2dy2).
Ainsi, 0 = 2(dx)d(dx) + 2xdxdy2, et donc dx d2x + x dx dy2 = 0. D'où l'expression d2x /dy2 = -x.
- Leibniz, 1694 : Actes des Savants de Leipzig de l'an 1694 : description du tracé de la ligne des sinus. [In Godefroy-Guillaume Leibniz, Oeuvre concernant le calcul infinitésimal, trad. Jean Peyroux, Paris : Blanchard, n.d., p. 35.]
- Marquis de l'Hôpital
(1661-1704), Analyse des infiniments petits, Pour
l'intelligence des lignes courbes, Paris, 1696.
On n'y retrouve aucune fonction trigonométrique.
- 1730-1748 : Euler (1707-1783), le véritable inventeur des fonctions trigonométriques. Le cercle de rayon 1 devint la norme en trigonométrie.
[Léonard Euler, Introduction à l'Analyse infinitésimale, trad. J.B. Labey, tome premier, Paris 1796. Chap. VIII, Des Quantités transcendantes qui naissent du Cercle. Première publication 1748, Lausanne.
D.J. Struik, A Source Book in Mathematics, 1200-1800, Cambridge, Mass : Harvard univ. Press, 1969, pp. 345-351.]
- Qu'advient-il des méthodes d'arpentage pendant
les XVIIe et XVIIIe siècle ?
Pour le savoir voir : Xavier Lefort, Arpentage et mathématiques au XVIIème, dans Evelyne arbin et al., Mathématiques arts et techniques au XVIIème siècle, Publications de l'Université du Maine, N° 4, 1987, pp. 255à 274.
- 1807 Fourier (1768-1830) utilise les séries trigonométriques pour représenter des fonctions.
- Au cours du siècle : définition d'ensembles, étude de l'intégrale comme une mesure de surface, notion générale de fonction. (Voir le tableau des liens historiques de l'évolution de la notion de fonction)
- Pour plus de détails,voir les articles de Louis Charbonneau dans le recueil de textes (pp. 4-7 à 4-15).
- Pour l'utilisation de l'analyse de Fourier : Bracewell, Jean-Baptiste Fourier, dans Les mathématiciens, Paris : Belin, 1996, pp. 86 à 95. Dans le même livre, il y a aussi un article sur Cantor, par Joseph Dauben, qui est intéressant (pp. 182-195).
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |