Atteindre l'inaccessible : Les mathématiques dans l'histoire

Le collège de Québec fondé en 1635 (avant 1878, date de sa démolition)

La chaire royale de mathématiques et d'hydrographie (1678-1759)

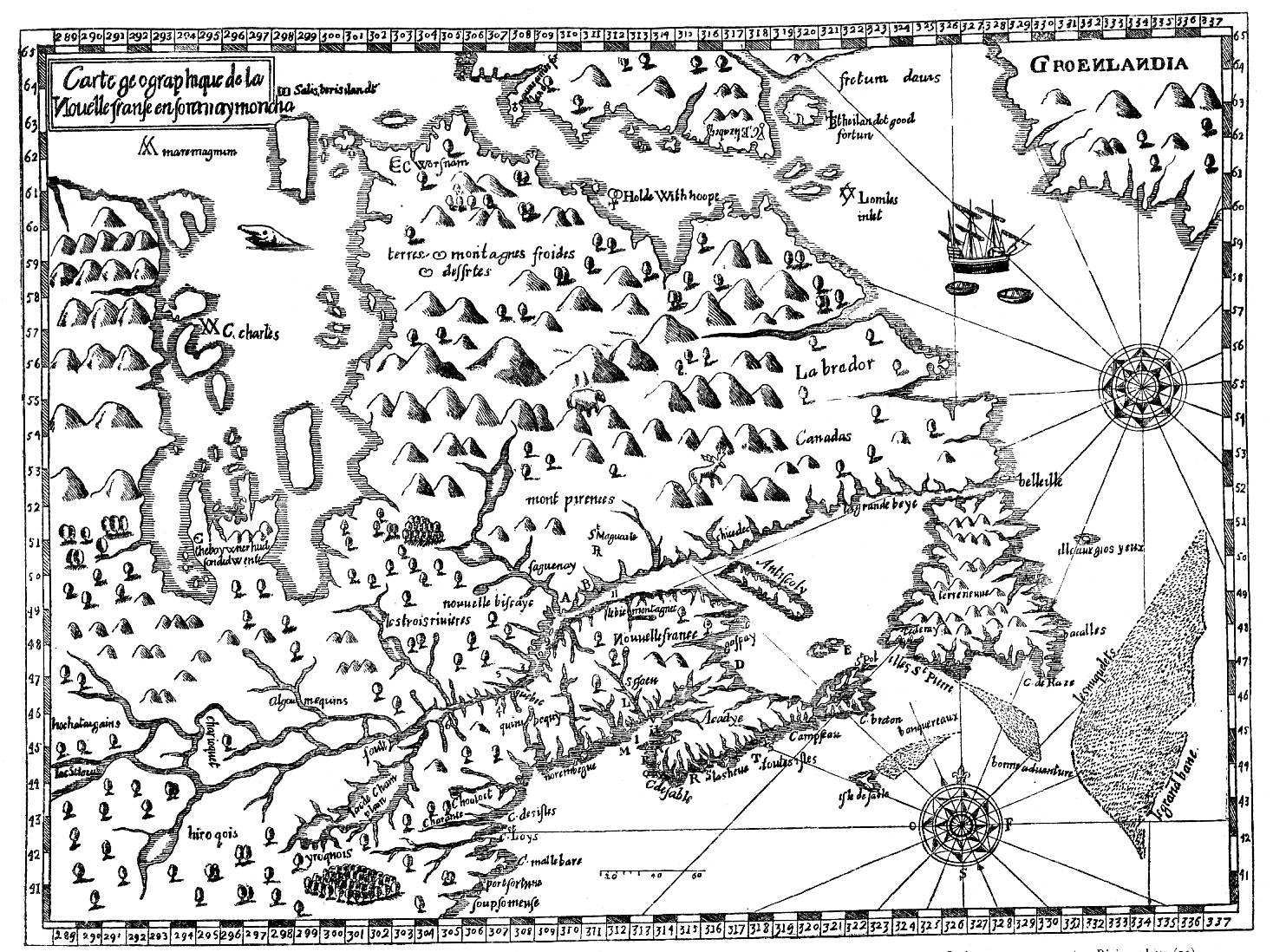
• Jean Bourdon (1601-1668)
• Martin Boutet de Saint-Martin (1616-1683) Premier titulaire [1678]
• Jean-Baptistie-Louis Franquelin (1652-1718), [1687-1692]
• Louis Jolliet (1645-1700), [1697]
• Jean Deshayes (?-1707), [1703-1706]
• Les jésuites de Québec : 1709-1759

Le collège de Québec (fondé en 1635, fermé en 1757)

• Le programme au XVII^e siècle (selon ce qu'on faisait en France)

Les humanités (6 ans)

• Mathématiques pures :

  • arithmétiques, algèbre, géométrie, trigonométrie rectiligne

• Mathématiques mixtes :

  • géométrie pratique : longimétrie, planimétrie, stéréométrie
  • mécanique : science des forces et de l'action des corps
  • hydrostatique
  • astronomie sphérique (mathématiques reliées aux globes célestes)
  • gnomonique
  • optique : perspective, dioptrique, catoptrique
  • traité de fortification (parfois)
  • pyrotechnie (parfois)
  
  

Recommandations de l'Abbé Sauri : Je conseillerois encore à Messieurs les professeurs de philosophie d'enseigner mes institutions au commencement du Cours, ou du moins, d'enseigner l'Arithmétique, les quatre premières règles de l'algèbre, avec les notions de Géométrie contenue dans le n° 1, p. 141 jusqu'au n° 7 p. 147 inclusivement. Cette attention mettra leurs écoliers en état de mieux entendre la Logique et la Métaphysique. Dans la Logique même, on parle souvent  de triangles, de cercles, &c. À de jeunes gens qui n'ont aucunes connoissances de ces figures; comment veut-on qu'ils entendent quelques choses aux explications du Professeur?