|
Autres représentations: définition en termes d'eccentricitéOn définit parfois les coniques comme des lieux géométriques, mais en utilisant le concept d'eccentricité e (qui est un nombre réel positif) : étant donné un point F (appelé foyer) et une droite d (appelée directrice), la conique sera l'ensemble des points P tels que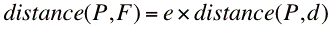 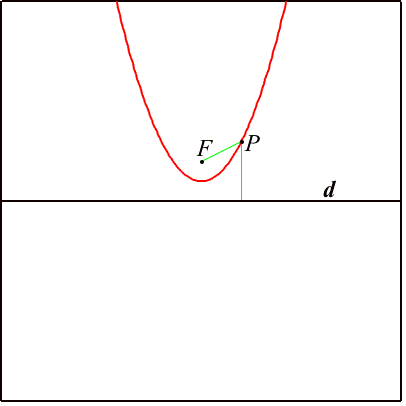 Remarquons que, lorsque e = 1, on retrouve la définition usuelle de la parabole en tant que lieu géométrique. On peut voir ci-dessous le résultat obtenu en faisant varier cycliquement l'eccentricité. 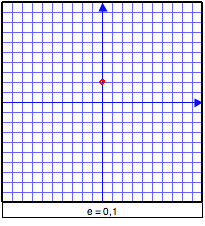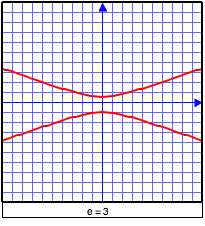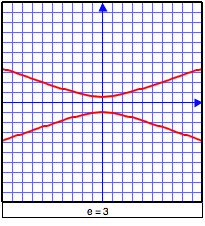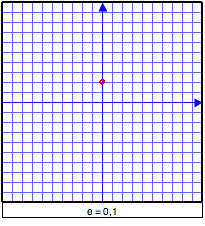 Notons ici que,
si P
= (x, y),
F = (0, a) et d est
l’axe des x,
la relation
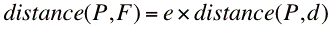 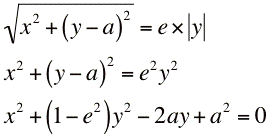 On se ramène donc à un cas particulier de l'équation générale des coniques: 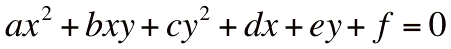 Appendice technologiqueComme d'habitude, les équations ont été formées dans l'éditeur d'équations de Word, puis enregistrées sous forme de fichier GIF. L'image du haut a été engendrée par une liste d'instructions dans Langage Graphique.Le GIF animé ci-dessus a été créé à partir d'images produites par une animation Langage Graphique, que nous avons assemblées dans un logiciel permettant de créer des fichiers GIF animés (par exemple Graphic Converter sur Macintosh, UnFREEz sur Windows, ou GIMP sur les deux plates-formes). |
