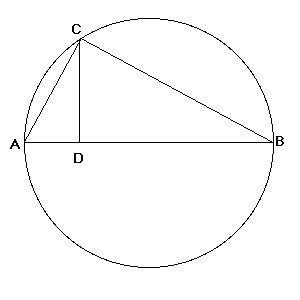MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Géométrie (2)
Au-delà du cercle et du compas
-
Pourquoi se limiter au cercle et au compas ?
Quatre raisons (selon Jean-CLaude Carrega, théorie des corps, La règle et le compas, Nouvelle édition, Paris : Herman, collection Formation des enseignants et formation continue, 1989, chap. I. Voir aussi Joëlle Delattre, Rudolf Bkouche, Pourquoi la règle et le compas ?, dans Historie de problèmes, histoire des mathématiques, Commission inter-IREM, Épistémologie et histoire des mathématiques, IREM de Lyon, 1992 (Pour ICME - Québec 92), pp.79-102.
-
Les courbes les plus simples, et les plus élégantes et parfaites, sont la droite et le cercle.
-
Influence de Platon et de son école, l'Académie.
-
Besoin de figures claires pour que les démonstrations soient convaincantes.
-
La découverte des incommensurables (irrationnels) : tracer l'hypothénuse d'un triangle rectangle isocèle peut se faire avec la règle et le compas.
-
-
Les quatre problèmes grecs : la règles et le compas sont insuffisants.
-
La quadrature du cercle
(Voir Euclide (format pdf,) livre douzième, prop. 1)
-
La duplication du cube (La légende de son origine)
-
Hippocrates de Chios (v. 470-410) : le problème se ramène à trouver deux moyennes proportionnelles entre 1 et 2, 1/x = x/y = y/2 => (1/x)3 = 1/2, donc x est le côté du cube qui a un volume double du cube de côté 1.
- AJOUT : Équerre de Platon (ne fonctionne pas)
- AJOUT : Mésolabe d'Ératosthène (ne fonctionne pas)
-
-
La trisection de l'angle
- Hippias (v. 460-400 av. notre ère) : la quadratrice :
-
La construction des polygones réguliers
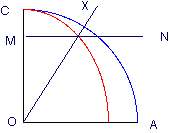
arcCOX / arcCOA = CM / CO
Cliquez ici pour une image dynamique (ne fonctionne pas)
Ces problèmes sont-ils résolubles par la règle et le compas ?
- La quadrature du cercle : NON - 1882 par Ferdinand Lindeman (1852-1939)... car pi est transcendant.
- La duplication du cube : NON - 1837 Pierre-Laurent Wantzel (1814-1848)... caractérisation algébrique des coordonnées des pints constructible à l'aide de la règle et du compas (suite aux travaux de Gauss et Descartes (1595-1650))
- La trisection de l'angle : NON - idem.
- La construction des polygones réguliers : conditions de constructibilité données par Gauss (1777-1855) (condition suffisante) en 1796, et Wantzel en 1837 (condition nécessaire).
-
Les coniques
-
Menechme (v. 380-320 av. notre ère) : cône à sommet droit.
-
Apollonius de Perga (v. 280-180 av. notre ère)
-
La parabole à partir du cône.
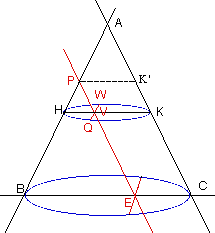 Considérons
un cône droit à base circulaire. La trace dans le plan
vertical (écran) est ABC. Coupons ce cône par un plan pour
lequel w = a
(C,est-à-dire que le plan de coupe est parralèle au côté du
cône). (P et E sont dans ce plan tout en étant dans le plan
vertical ABC).
Considérons
un cône droit à base circulaire. La trace dans le plan
vertical (écran) est ABC. Coupons ce cône par un plan pour
lequel w = a
(C,est-à-dire que le plan de coupe est parralèle au côté du
cône). (P et E sont dans ce plan tout en étant dans le plan
vertical ABC). 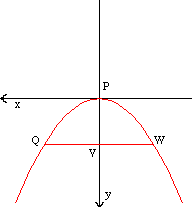 La
trace du cône dans le plan sécant est la courbe passant
passant par les point P, Q, W. Si, par ailleurs, on coupe le
cône par un plan parallèle à la base du cône et si ce plan
horizontal coupe le plan sécant sous le point P, la trace du
cône dans ce plan horizontal est un cercle. Le segment QW
est dans l'intersection de ce plan horizontal et du plan
sécant. Par ailleurs, les points Q et W sont aussi sur le
cône. Ils sont donc aussi sur la courbe qui est la trace du
cône dans le plan sécant. (Q et W sont des points de la
parabole).
La
trace du cône dans le plan sécant est la courbe passant
passant par les point P, Q, W. Si, par ailleurs, on coupe le
cône par un plan parallèle à la base du cône et si ce plan
horizontal coupe le plan sécant sous le point P, la trace du
cône dans ce plan horizontal est un cercle. Le segment QW
est dans l'intersection de ce plan horizontal et du plan
sécant. Par ailleurs, les points Q et W sont aussi sur le
cône. Ils sont donc aussi sur la courbe qui est la trace du
cône dans le plan sécant. (Q et W sont des points de la
parabole). Nous cherchons à déterminer une relation qui nous permette d'affirmer que la trace du cône dans le plan sécant est bien une parabole. Pour faire cela, étant donné un point Q quelconque de cette trace, il suffit d'établir une relation entre le segment QV et le segment PV, car ces deux segments sont orthogonaux (car les segments PQ et PV sont dans le plan sécant et perpendiculaires l'un à l'autre, étant donné que le cercle HWKQ et que le plan sécant sont perpendiculaires au plan vertical [par construction, voir le cours Géométrie II]) et donc que l'un peut jouer le rôle de x et l'autre le rôle de y. C'est comme si on placait dans le plan sécant un plan cartésien orthogonal d'origine P et orienté comme le montre la figure à gauche. Alors PV joue le rôle de y et QV joue le rôle de x. Nous cherchons donc une relation entre PV et QV qui soit de la forme mQV2 = a x mPV, où a est une constante qu'il nous faudra exprimer en termes géométriques.
Remarquons d'abord que si on regarde le cercle HQKW d'en haut, on voit la figure suivante.

 Dans
cette figure, dans le cercle HQKW, on a la relation
suivant :
Dans
cette figure, dans le cercle HQKW, on a la relation
suivant :
mQV2 = mHV x mVK. (*)
(Car les points H, Q, et K forment un triangle rectangle, HK étant le diamère du cercle. Or, dans un traingle rectangle , la hauteur élevée sur l'hypothénuse est moyenne proportionnelle entre les deux segments déteminés par la hauteur sur l'hypothénuse.)Il nous faut maintenant faire apparaître PV dans la partie de droite de cette équation.
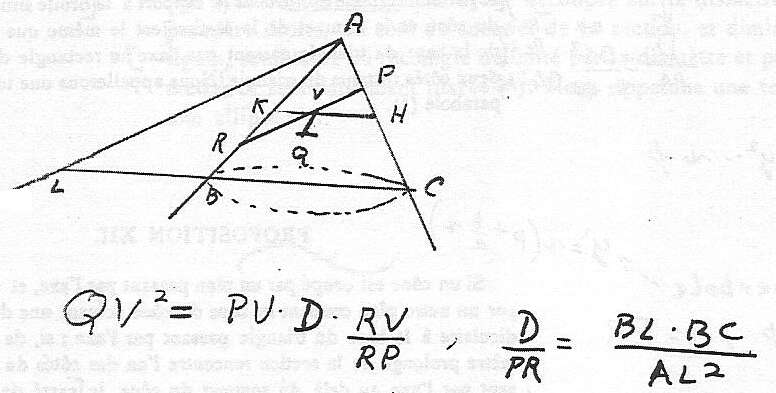
- Considérons les triangles semblables dans le plan vertical ABC:
- Le triangle PHV est semblable au triangle ABC. On a donc :
- Le triangle PAK' est semblable au triangle ABC, où K' est la point d'intersection de la parallèle à la droite dBC passant par P et de la génératrice du cône dAC. On a donc :
- En utilisant les deux proportions trouvées en 2, on peut
exprimer mHV et mVK
(mVK = mPK', car le quadrilatère PK'KV est un parallélogramme) comme suit : - mHV = mBC x mPV / mAC
- mPK' = mVK = mBC x mAP / mBA.
- En remplaçant dans (*), on obtient :
mQV2 = mBC x mPV x mBC x mAP / (mAC x mBA).
En réorganisant cet expression, pour mettre en évidence le segment PV, on a
mQV2 = mPV x [mBC x mBC x mAP / (mAC x mBA)] = mPV x [mBC2 / (mAC x mBA)] x [ mAP]. (**)
- L'expression (**) correspond à ce que je cherche. En effet, si je note mQV par x et mPV par y, j'ai comme expression
HV/PV = BC/AC.
PK'/AP = BC/BA.
x2 = y x [mBC2 / (mAC x mBA)] x [ mAP] = y x k, où on aimerait que k soit une constante.
Voyons donc si k est effectivement une constante, c'est-à-dire qu'il a une valeur qui ne dépend pas de la position de Q sur la parabole. D'abord notons que k est le produit de deux facteurs.
- Le premier facteur, [mBC2 / (mAC x mBA)], est formé de segments qui sont en fait caractéristiques du cône. En effet, les segments AB, AC et BC dépendent simplement de l'ouverture du cône au sommet A. Donc ce facteur change de valeur avec la plus ou moins grande ouverture du cône en A. C'est donc une constante qui ne dépend pas de la position de Q sur la parabole, mais qui dépend du cône.
- Le second facteur, [mAP], ne dépend pas du cône comme tel, mais plutôt de la position du plan sécant puisqu'il donne la distance entre le sommet du cône et le point où le plan « commence » à couper le cône. Il caractérise donc la position de plan sécant par rapport au cône.
k est donc vraiment une constante, qui contient de l'information à la fois sur le cône et le plan sécant.
Exemple : la cas du cône « équilatéral »
Afin de fixer les idées, considérons un cône qui simplifiera au moins un des deux facteurs de la constante k. Ainsi, un cône qui ferait en sorte que le premier facteur , [mBC2 / (mAC x mBA)], soit 1 serait un avantage pour voir ce qui se passe. Pour cela, il faut que mBC2 = (mAC x mBA). Pour cela, il suffit de prendre un cône dont la trace dans le plan écran soit telle que mAB = mBC = mCA. Il suffit donc de prendre un cône dont la trace dans le plan écran avec un cercle de base soit un triangle équilatérale. Alors, dans ce cas,
k = mAP.
Autrement dit, la constance k égale précisément la distance entre le sommet du cône et le point qui est à l'intersection de la droite qui est la trace du plan sécant dans le plan écran et la trace du cône dans le plan écran.
On peut conclure de là que la parabole d'équation y = x2, pour lequel donc k = 1, correspond exactement à la trace d'un cône « équilatéral » dans un plan sécant, tel que w = a, qui coupe le cône « équilatéral » à une unité du sommet du cône.
Remarque : Les unités de mesure utilisées dans le plan cartésien où on trace la parabole d'équation y = x2 doivent être les mêmes que celles utilisées pour la mesure du cône. Autrement, on aurait pas exactement la même parabole (avec les même mesures) dans les deux cas, mais deux paraboles semblables.
-
Décrire les coniques : Les Coniques
Parabole (Livre I proposition XI)
QV2 = PV x D, où D est tel que D : PA = BC2 : AC x AB

Texte d'Apollonius
Si un cône est coupé par un plan passant par l'axe [plan ABC], et s'il est coupé par un autre plan coupant la base du cône suivant une droite perpendiculaire à la base du triangle passant par l'axe [plan PVQ]; si, de plus, le diamètre [PE] de la section est parallèle à l'un des côtés du triangle passant par l'axe, le carré de toute droite menée de la section du cône, parallèlement à la section commune du plan sécant et de la base du cône, jusqu'au diamètre de la section, équivaut au rectangle délimité par la droite qu'elle découpe sur le diamètre, du côté du sommet de la section, et par une certaine droite dont le rapport à la droite située entre l'angle du cône et le sommet de la section est le même que celui du carré de la base du triangle passant par l'axe au rectangle délimité par les deux côtés restants du triangle. Nous appelleronts une telle section une parabole.
-
L'ellipse
L'hyperbole

N.B. Asymtote et symptôme ont la même étymologie : du grec sun (avec) et pitein (tomber). Le a est un privatif.
Comment découvrir : l'analyse des anciens
Pappus
d'Alexandrie (290-350),
La Collection Mathématique, Trad. Paul ver Eecke, Paris 1933, p.
477.
Livre VII
Le champ de l'analyse, tel que je le conçois, mon fils Hermodore, est la matière particulière dont disposent ceux qui, après avoir acquis les éléments vulgaires, veulent puiser dans les lignes la puissance de trouver les problèmes qui leurs sont proposés. C'est en suivant la voie de l'analyse [analusiV, la résolution] et de la synthèse [suntesiV, la construction] que cette matière a été traitée par trois hommes : Euclide, auteur des Éléments, Apollonius de Perge et Aristée l'Ancien. L'analyse est donc la voie qui part de la chose cherchée, considérée comme étant concédée, pour aboutir, au moyen des conséquences qui en découlent, à la synthèse de ce qui a été concédée. En effet, supposant, dans l'analyse, que la chose cherchée est obtenue, on considère ce qui dérive de cette chose et ce dont elle est précédée, jusqu'à ce que, revenant sur ses pas, on aboutissent à une chose déjà connue ou qui rentre dans l'ordre des principes ; et l'on nomme cette voie l'analyse en tant qu'elle constitue un renversement de la solution. Dans la synthèse, au contraire, supposant la chose finalement perçue par l'analyse comme étant déjà obtenue, et disposant dès lors ses conséquences et ses causes dans leur ordre naturel, puis, les rattachant les unes au autres, on aboutit en dernier ressort à construire la chose cherchée ; et c'est ce que nous appelons la synthèse.
Exemple 1
(Trouver une démonstration d'une propriété)
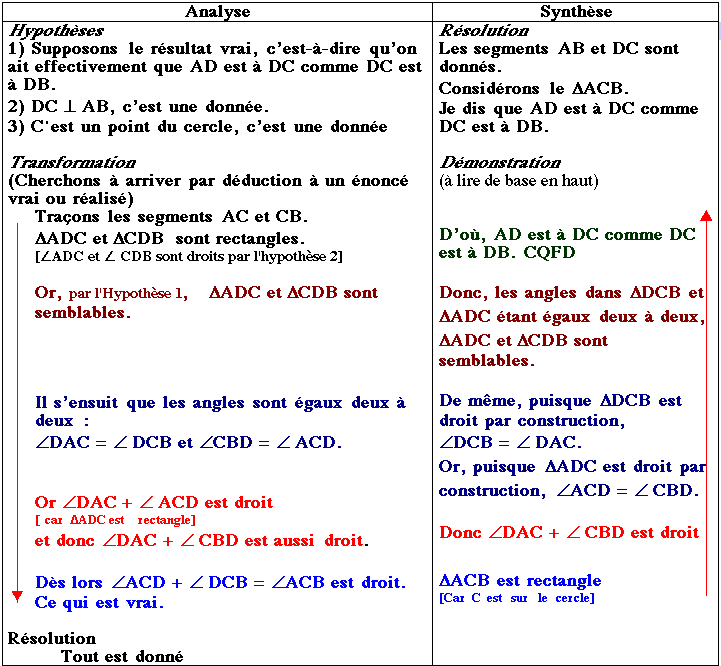
Soit un cercle de diamètre AB. Soit DC, une perpendiculaire abaissée du point C du cercle sur AB. Alors, AD est à DC comme DC est à DB.
Exemple 2
(Trouver une construction)
Pappus, Collection mathématique, Livre VII, proposition
105
Pappus d'Alexandrie, La collection mathématique, trad. de
Paul ver Eecke, Paris, Bruges, 1933, t. II, p. 640-642.
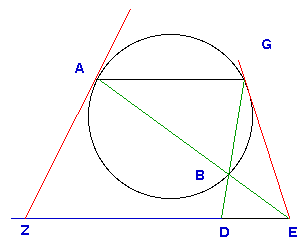
Le cercle ABG étant donné de position, et deux points D, E étant donnés extérieurs au cercle. Trouver un point B sur le cercle tel que EB prolongé coupe le cercle en A et DB prolongé coupe le cercle en G, de telle sorte que le segment AG soit parallèle à DE.
Analyse |
Synthèse |
Hypothèses
Transformation
Résolution
|
(Lire de bas en haut) |
Archimède (287-212) et l'usage de la mécanique
La méthode relative aux théorèmes mécaniques
Rappel préliminaire Le principe du levier : Fd = F'd' ou F est à F' comme d' est à d.
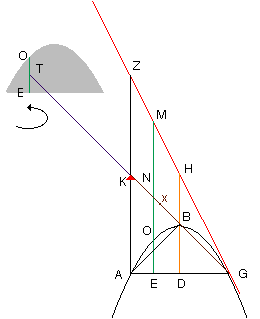
Énoncé : Soit AG la base d'une parabole. Trois fois le secteur de parabole ABG et quatre fois le triangle ABG ont la même aire, où AD = DG et BD est | | au diamètre de la parabole.
|
Démonstration : Soient GZ tangent à la parabole en G et AZ | | au diamètre.
1) Par des théorèmes sur les paraboles, on a DB = BH Et donc l'aire du triangle AZG est égal à quatre (4) fois l'aire du triangle ABG.
2) Par un théorème sur les paraboles, si O est un point quelconque de la parabole, on a ME est à EO comme GA est à AE (ME:EO :: GA:AE) Par ailleurs, par les triangles semblables, GA est à AE comme GK est à KN (GA:AE ::GK:KN) Donc, ME est à EO comme GK est à KN (ME:EO :: GK:KN) (Pensons au levier ici).
3) Prolongeons le segment GK au delà de K jusqu'à un point T tel que GK = KT. On a alors, par le point 2), que ME est à EO comme KT est à KN.
4) On peut interpréter cette proportion, par le principe du levier, comme voulant dire que le segment OE placé à T équilibre le segment ME placé à N, avec pour pignon le point K.
5) Prenant alors successivement tous les points "O" de la parabole délimitant le secteur et considérant que le secteur ABG est composé des segments "OE" accolés les uns aux autres et que le triangle AZG est de même composés des segments "ME" accolés les uns aux autres, on peut dire que le secteur ABG placé à T, perpendiculaire au plan du secteur (donc perpendiculaire à l'écran) équilibre le triangle AZG, autour du pignon K. Autrement dit, si x est le centre de gravité du triangle AZG, on a que le triangle AZG est au secteur ABG comme TK est à Kx.
6) Or le centre de gravité du triangle AZG se trouve sur GK à un point x tel que Kx soit le tiers de GK. Il en résulte donc que le triangle AZG est au secteur ABG comme TK est au tiers de KG, autrement dit comme 3 est à 1. Donc le secteur ABG est trois fois plus petit que le triangle AZG. Or, comme on l'a dit en 1), le triangle AZG vaut quatre fois le triangle ABG. Il en découle que trois fois le secteur de parabole ABG correspond à la même aire que quatre fois le triangle ABG. CQFD
|
|
Archimède continue en disant : « Ce que nous venons de dire ne démontre sans doute pas ce qui précède, mais donne jusqu'à un certain point l'idée que la conclusion est juste. C'est pourquoi, reconnnaissant nous-même que la conclusion n'est pas démontrée, mais ayant dans l'idée qu'elle est exacte, nous donnerons en son lieu la démonstration géométrique que nosu avons trouvée et déjà publiée.» (Preuve synthétique publiée dans le livre De la Quadrature de la Parabole.)
La fin des mathématiques grecques - Réfléxion à partir de la chronologie.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |