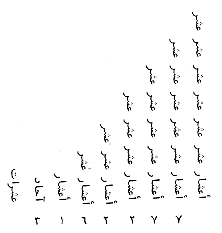Du monde arabo-musulman à la Renaissance : Religion et marchands
as-Samaw'al (v. 1130-1180) : Invention des fractions décimales
- As-Samawal, dans son traité Traité
d'arithmétique (1172), consacré à l'extraction des racines
et la résolution par approximation des équations algébriques.
Dans le cadre de l'étude des techniques d'approximation des racines d'un polynôme, là naîtront les fractions décimales.
Voyons d'abord comment les polynômes étaient représentés.
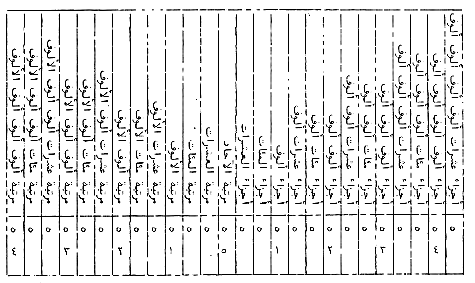
Considérons le tableau suivant :
En écrivant le coefficient des puissances de l'inconnue dans les colonnes correspondantes, on peut écrire une expression comme 3x2 + 5 + 1/x, ainsi :
Dans ce contexte, la règle des exposants, correspondant à xnxm = xn+m, s'énonce ainsi :
« Si les deux puissances sont de part et d'autre de l'unité, à partir de l'une d'elles nous comptons en direction de l'unité, le nombre des éléments du tableau qui séparent l'autre puissance de l'unité, et le nombre est du côté de l'unité. Si les deux puissances sont du même côté de l'unité, nous comptons en direction opposée à l'unité. »
La dernière section du traité est consacrée à cette nouvelle forme de calcul. Elle est intitulée :
« Au sujet de la position d'un principe unique par lequel on peut déterminer toutes les opérations de la partition (al-Tafriq) qui sont la division, l'extraction de la racine carrée, l'extraction d'un côté par toutes les puissances, et la correction de toutes les fractions qui apparaissent dans ces opérations, indéfiniment. »En identifiant les unités à la puissance zéro de l'inconnue, as-Samawal peut énoncer cette règle et même l'étendre au cas où x n'est pas une inconnue mais une valeur numérique… comme 10. Par le transfert des règles comme celle-ci des polynômes aux tableaux à base 10, il obtient un système permettant de calculer avec les décimaux.
0 : parties des unités
1 (à droite) : parties des dizaines
1 (à gauche) : parties des dizaines (en fait les dixièmes)Voici la racine carrée de 10 :
Pour prononcer les fraction, il les ramène à une fraction sur le dénominateur de la plus petite fractions décimale. Ainsi, la racine carrée de 10 se lit 3 unités plus 162277 parties de 1 000 000 parties. (À la façon habituelle de nommer les fractions chez les Arabes.) Dans la notation, il sépare la partie décimale de la partie entière par un signe, comme une barre verticale.
On voit donc que les fractions décimales viennent de la pratique des opérations sur les polynômes exprimés sous forme de tableaux.