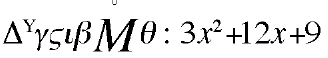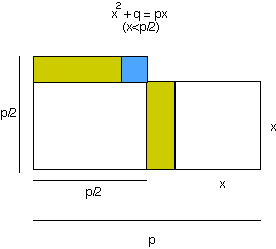MAT 6221
Bas de la page
prof. Louis Charbonneau
UQAM
Algèbre (1)
Jusqu'à la Renaissance
Un survol de l'histoire de l'algèbre
-
L'algèbre des règles non-explicites
- En Mésopotamie
- En Égypte
-
Les règles algébriques dans la géométrie grecque
-
Le retour du numérique : Diophantes (v. 200-284)
-
L'algèbre arabe
- Al-Khwarizmi (v. 780-850)
- Le courant arithmético-algébrique : al-Karagi (953-1029) et as-Samaw'al (1130-1180)
- Le courant gréométrico-algébrique : al-Khayyam (1048-1131)
-
L'algèbre des marchands au Moyen Âge
-
Vers un symbolisme fonctionnel : La Renaissance
- Multiplicité des symboles
- La résolution des équations du 3e degré : Cardan (1501-1576) et les nombres complexes
-
François Viète (1542-1603) : l'algèbre obtient ses lettres de noblesses
- Algèbre et analyse
- Un symbolisme en devenir
- Une théorie des équations
- Les lettres de noblesse
-
Le retour à la géométrie : René Descartes (1596-1650) et la « géométrie analytique »
1. L'algèbre des règles non-explicites
- Babylone Les équations du second degré
- Trois problèmes du second degré et leur
solution (Tiré de Dedron, Itard, Mathématique
et Mathématiciens)
Premier problème
J'ai additionné la surface et le côté de mon carré : 45'.
Tu poseras 1 l'unité. Tu fractionneras en deux 1 : 30'. Tu croiserass 30' et 30' : 15'. Tu ajouteras 15' à 45' : 1. C'est le carré de 1. Tu soustrairas 30', que tu as croisé, de 1 : 30', le côté du carré.
x2 + x = 45° (pour nous : x2 + bx = -c)
pour nous : x = -b/2 + RacCarré((b/2)2 - c)
Second problème
J'ai soustrait de la surface le côté de mon carré : 14`30°.
Tu poseras 1, l'unité. Tu fractionneras en deux 1 : 30'. Tu croiseras 30' et 30' : 15'. Tu ajouteras à 14`30° : 14`30° 15'. C'est le carré de 29°30'. Tu ajouteras 30', que tu as croisé, à 29°30' : 30°, le côté du carré.
x2 - x = 14`30° (pour nous : x2 + bx = -c)
pour nous : x = b/2 + RacCarré((b/2)2 - c)
Troisième problème
J'ai additionné sept fois le côté de mon carré et onze fois la surface : 6°15'.
Tu inscriras 7 et 11. Tu porteras 11 à 6°15' : 1`8°45'. Tu fractionneras en deux 7 : 3°30'. Tu croiseras 3°30' et 3°30' : 12°15'. Tu ajouteras à 1`8°45' : 1`21°. C'est le carré de 9. Tu soustrairas 3°30', que tu as croisé, de 9 : tu inscriras 5°30. L'inverse de 11 ne peut être dénoué. Que dois-je poser à 11 qui me donne 5°30' ? 30', son quotient. Le côté du carré est 30'.
Énoncé : 7x + 11x2 = 6°15'
(RacCarré((7/2)2 + 11•6°15') - 7/2) = 11x
11x = 5°30'
La division se fait en résolvant 11x = 5°30'
x = 30'
Pour nous : si bx + ax2 = -c
(RacCarré((b/2)2 - ac) - b/2) = 11x - Un autre exemple (*)
La somme est 32, l'aire est 252
Longueur 18, largeur 14
Prenez la demie de 32 : 16. !6 fois 16 est 256. 256 moins 252 est 4. La racine carré de 4 est 2. 16 et 2 font 18, largeur. 16 moins 2 est 14, largeur.
- Système d'équation du second degré.
- Trois problèmes du second degré et leur
solution (Tiré de Dedron, Itard, Mathématique
et Mathématiciens)
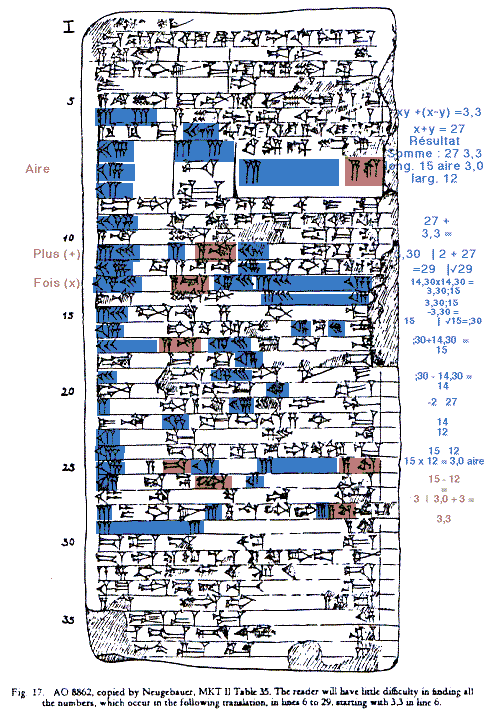
B. L. van der Waerden, Science Awakening, New York, : Oxford University Press, p. 64.
-
Égypte : La règle de fausse position (Voir le cours sur les fractions)
2. Les règles algébriques de la géométrie grecque
Un premier exemple : les Notions communes des Éléments d'Euclide
Un second exemple : les premières propositions du livre II des Éléments d'Euclide
Pour les textes ci-dessus, voir le premier cours sur la géométrie
Un autre exemple : la proposition III-35 des Éléments d'Euclide
Si deux cordes d'un cercle sont sécantes, le rectangle contenu par les segmens partiels de l'une est égal au rectangle contenu par les segments partiels de l'autre.
Demonstration :
( . . . )
[Utilisant nos notations, la fin de la démonstration va comme suit
: ]
a b + c2 = d2
Ajoutons aux deux membres l'aire e2 ; il vient :
a b + c2 + e2 = d2 + e2.
Mais c2 + e2= f2 and d2 + e2 = g2.
Donc a b + f2 = g2.
Et g2 = h2.
Donc a b + f2 = h2.
Pour les mêmes raisons nous avons de même : a' b' + f2 = h2.
Mais nous avons prouvé que a b + f2 = h2,
donc a' b' + f2 = a b + f22.
après élimination du terme commun f2 :
a' b' = a b. Q.E.D.
3. Le retour du numérique : Diophantes (v. 200-284)
Notation syncopée : des lettres pour une inconnue et pour les puissances
La règle des signes : elle est donnée, mais sans explicitation.
Activité : Comparer le problème (*) babylonien de la page 27 au problème I-XXVII de Diophante.
Livres arithmétiques. Livre I, problème XXVII
Trouver deux nombres tels que leur somme et leur produit forment des nombres donnés.
Il faut toutefois que le carré de la demi-somme des nombres à trouver excède d’un carré le produit de ses nombres : chose qui est d’ailleurs figurative.
Proposons donc que la somme des nombres forme 20 unités, et que leur produit forme 96 unités.
Que l’excédent des nombres soit 2 arithmes. Dès lors, puisque la somme des nombres est 20 unités, si nous la divisons en deux parties égales, chacune des parties sera la moitié de la somme, ou 10 unités. Donc, si nous ajoutons à l’une des parties, et si nous retranchons de l’autre partie, la moitié de l’excédent des nombres, c’est-à-dire 1 arithme, il s’établit de nouveau que la somme des nombres est 20 unités, et que leur excédent est 2 arithmes. En conséquence, posons que le plus grand nombre est 1 arithme augmenté des 10 unités qui sont la moitié de la somme des nombres; donc le plus petit nombre sera 10 unités moins 1 arithme, et il s’établit que la somme des nombres est 20 unités, et que leur excédent est 2 arithmes.
Il faut aussi que le produit des nombres forme 96 unités. Or leur produit est 100 unités moins 1 carré d’arithme; ce que nous égalons à 96 unités, et l’arithme devient 2 unités. En conséquence, le plus grand nombre sera 12 unités, le plus petit sera 8 unités, et ces nombres satisfont à la proposition.
Livres arithmétiques. Livre I, Problème XXVIII
Trouver deux nombres tels que leur somme et la somme de leurs carrés forment des nombres donnés.
Il faut toutefois que le double de la somme des carrés des nombres excède d’un carré le carré de la somme des nombres, chose qui est aussi figurative.
Proposons donc que la somme des nombres forme 20 unités, et que la somme de leurs carrés forme 208 unités.
Que la différence des nombres soit 2 arithmes. Que le plus grand nombre soit 1 arithme, augmenté de nouveau de la moitié de la somme des nombres, c’est-à-dire de 10 unités, et que le plus petit nombre soit 10 unités moins 1 arithme; ce qui établit de nouveau que la somme des nombres est 20 unités, et que leur différence est 2 arithmes.
Il faut encore que la somme des carrés des nombres forme 208 unités. Mais la somme de leurs carrés forme 2 carrés d’arithme plus 200 unités; ce que nous égalons à 208 unités, et l’arithme devient 2 unités.
Revenant à ce que nous avons posé, le plus grand nombre sera 12 unités, le plus petit nombre sera 8 unités, et ces nombres satisfont à la proposition.
Livres arithmétiques. Livre III, Problème XXVIII
Trouver trois nombres tels que le carré de la somme de ces trois nombres, retranché de chacun de ces nombres, forme un carré.
Posons que la somme des trois nombres est 1 arithme, et que le carré de cette somme est 1 carré d’arithme. Que les trois nombres soient 2 carrés d’arithme, 5 carrés d’arithme et 10 carrés d’arithme. On établit ainsi que chacun des nombres, diminué du carré de la somme des trois nombres, c’est-à-dire diminué de 1 carré d’arithme, forme un carré.
Dès lors, puisque le carré de la somme des trois nombres a évidemment comme racine la somme des trois nombres, il s’ensuit que la somme des trois nombres est 1 arithme. Or, cette somme est aussi 17 carrés d’arithme; donc, l’arithme devient 1/17, et le carré d’arithme 1/289. Le premier nombre sera 2/289; le second sera 5/289; le troisième 10/289, et ces nombres résolvent la proposition.
4. L'algèbre arabe
-
Al-Khwarizmi (v. 780-850) Carte Biographie
- La tradition du calcul des héritage:
- Le Coran, Sourate 4, v. 11 et 12 (du
site maintenant non disponible :
http://callisto.si.usherb.ca/~amus/coran/4.html)
11.
 Voici
ce qu'Allah vous enjoint au sujet de vos enfants :
au fils, une part équivalente à celle de deux
filles. S'il n'y a que des filles, même plus de
deux, à elles alors deux tiers de ce que le défunt
laisse. Et s'il n'y en a qu'une, à elle alors la
moitié. Quant aux père et mère du défunt, à chacun
d'eux le sixième de ce qu'il laisse, s'il a un
enfant. S'il n'a pas d'enfant et que ses père et
mère héritent de lui, à sa mère alors le tiers. Mais
s'il a des frères, à la mère alors le sixième, après
exécution du testament qu'il aurait fait ou paiement
d'une dette. De vos ascendants ou descendants, vous
ne savez pas qui est plus près de vous en utilité.
Ceci est un ordre obligatoire de la part d'Allah,
car Allah est, certes, Omniscient et Sage.
Voici
ce qu'Allah vous enjoint au sujet de vos enfants :
au fils, une part équivalente à celle de deux
filles. S'il n'y a que des filles, même plus de
deux, à elles alors deux tiers de ce que le défunt
laisse. Et s'il n'y en a qu'une, à elle alors la
moitié. Quant aux père et mère du défunt, à chacun
d'eux le sixième de ce qu'il laisse, s'il a un
enfant. S'il n'a pas d'enfant et que ses père et
mère héritent de lui, à sa mère alors le tiers. Mais
s'il a des frères, à la mère alors le sixième, après
exécution du testament qu'il aurait fait ou paiement
d'une dette. De vos ascendants ou descendants, vous
ne savez pas qui est plus près de vous en utilité.
Ceci est un ordre obligatoire de la part d'Allah,
car Allah est, certes, Omniscient et Sage. 12. Et à vous la moitié de ce laissent vos épouses, si elles n'ont pas d'enfants. Si elles ont un enfant, alors à vous le quart de ce qu'elles laissent, après exécution du testament qu'elles auraient fait ou paiement d'une dette. Et à elles un quart de ce que vous laissez, si vous n'avez pas d'enfant. Mais si vous avez un enfant, à elles alors le huitième de ce que vous laissez après exécution du testament que vous auriez fait ou paiement d'une dette. Et si un homme, ou une femme, meurt sans héritier direct, cependant qu'il laisse un frère ou une soeur §, à chacun de ceux-ci alors, un sixième. S'ils sont plus de deux, tous alors participeront au tiers, après exécution du testament ou paiement d'une dette, sans préjudice à quiconque. (Telle est l') Injonction d'Allah ! Et Allah est Omniscient et Indulgent.
- un problème et sa solution
- Le Coran, Sourate 4, v. 11 et 12 (du
site maintenant non disponible :
http://callisto.si.usherb.ca/~amus/coran/4.html)
- La résolution des équations : Précis
sur le calcul de al-jabr et al-muqabala

- Les six types canoniques pour résoudre les équations
- Exemple de problème du cinquième type ( A.P. Youschkevitch, Les mathématiques arabes (VIIIe - XVe siècles), Paris : Vrin, 1976.)
- Les démonstrations de la justesse des règles de résolution (cinquième type)
- Mots provenants d'al-Khwarizmi : algèbre, algorithme,
- Abu Kamil (v. 850-930), premier disciple
d'al-Khwarizmi
- Utilisation des irrationnels. Ex. ¯a ±¯b = ¯(a+b ± 2¯ab)
- Non respect de l'homogénéité des expressions
Un musulman décède en laissant sa femme et ses deux filles, ainsi que son père et sa mère. Selon les prescriptions du Coran, les biens du défunt devraient être réparti ainsi :
Épouse le huitième
Mère le sixième
Père le sixième
Les filles les deux tiers.
Mais la somme de ces fractions (27/24) dépasse l’unité. Que faire ?
Le compromis proposé est de diviser l’ensemble de l’héritage en 27 parts et de les répartir ainsi :
Épouse 3 parts
Mère 4 parts
Père 4 parts
Les filles 16 parts.Est-ce une bonne solution ?
Pour se ramener à une forme connue :
2x2 + 100 - 20x = 58
Donne par al-jabr (remplissage, restauration)
2x2 + 100 = 20x + 58puis par al-muqabala (balancement, comparaison)
2x2 + 42 = 20xet par division par deux x2 + 21 =10x
1) ax2 = bx 4) ax2 + bx = c 2) ax2 = c 5) ax2 + c = bx 3) bx = c 6) bx + c = ax2 Djebbar propose de parler plutôt, pour 6 par exemple, de
« b fois racine de x carré + c = ax »(Figure ci-contre : Ahmed Djebbar, Le nombre, la racine et le bien, in Cahier de Science & Vie, No 56, avril 2000, 45. )
Activité : Comparer la solution du problème I-XXVII de Diophante (p. 26) à la solution du premier problème d'al-Khwarizmi (p. 69).
Quel sera le montant d'argent (mal) qui lorsqu'on lui ajoute 21 dirhams équivaut à 10 racines de ce montant ?Divise en deux les racines, ce qui donne 5; multiplie 5 par lui-même, tu obtiens 25; retire les 21 qui sont ajoutés au carré; il reste 4; extrais la racine - cela donne 2 - et retire-la de la moitié de la racine, c’est-à-dire de 5; il reste 3; c’est la racine du carré que tu cherches et le carré est 9. Si tu le désires, ajoute cela à la moitié de la racine, ce qui donne 7, qui est la racine du carré que tu cherches et dont le carré est 49. Si tu rencontres un problème qui se ramène à ce cas, examine alors sa justesse à l’aide de l’addition; si tu ne le peux, tu obtiendras certainement (la solution) à l’aide de la soustraction. Parmi les trois cas dans lesquels on doit diviser en deux les racines, c’est le seul où l’on se serve de l’addition et de la soustraction. Sache en outre que si dans ce cas, tu divises en deux la racine, que tu la multiplies par elle-même et que le produit soit plus petit que les dirhams qui sont ajoutés au carré, alors le problème est impossible. Mais s’il est égal aux dirhams, la racine du carré est égale à la moitié de la racine, sans qu’on ajoute ou retire quoi que ce soit.
(p-x)x = q
q + carré bleu = (p/2)2,
d'où le côté du carré bleu est p/2 - x
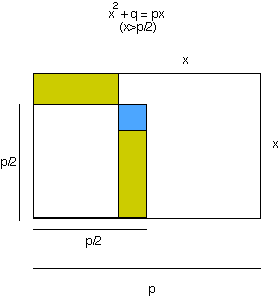
(p-x)x = q
q + carré bleu = (p/2)2,
d'où le côté du carré bleu est x - p/2Troisème cas : x = p/2.(Quoi faire avec ?)
-
Le courant arithmético-algébrique : Al-Karagi (953-1029) et as-Samaw'al (v. 1130-1180)
- Al-Karagi : développement d'une arithmétique de l'inconnue
- As-Samawal, un disciple d'al-Karagi(Illustrations tirées de R. Rashed, Entre artithmétique et algèbre, Recherches sur l'histoire des mathématiques arabes, Paris : Belles-Lettres, 1984, p. 143, 144 et 127.)
Depuis la représentation des polynômes à celle des fractions décimales
Les fractions décimales
« Au sujet de la position d'un principe unique par lequel on peut déterminer toutes les opérations de la partition (al-Tifriq) qui sont la division, l'extraction de la racine carrée, l'extraction d'un côté pour totues les puissances, et la correction de toutes les fractions qui apparaissent dans ces opértations indéfiniment. »
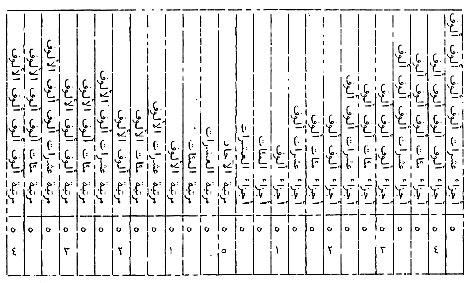
0 : parties des unités
1 (à droite) : parties des dizaines
1 (à gauche) : parties des dizaines (en fait les dizièmes)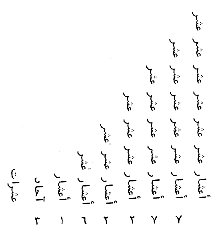

-
Le courant gréométrico-algébrique : al-Khayyam (1048-1131) carte
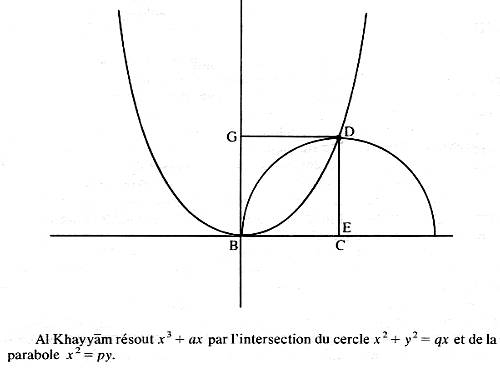
La résolution des équations du troisième degré par l'intersection de courbes.
Amy Dahan-Dalmedico, Jeanne Peiffer, Routes et Dédales, Paris, Montréal : Études Vivantes, 1982, p. 88.
Notation maghrébine (Le manuscrit mathématique de Jerba, par Mahdi Abdeljaouad)
5. L'algèbre des marchands au Moyen Âge
-
Les représentations au Bas Moyen Âge
-
À partir du XIIIe siècle : La floraison, l'abondance et l'efficacité des représentations (Ligne du temps)
-
-
Professionnalisation :
-
Musique :
Notation musicale, la polyphonie -
Abaquistes (math. des marchands) :
Nombres arabes, le calcul avec les nombres, mais surtout, la comptabilité à deux entrées -
Universités : classification et organisation des livres, rationalité
-
Navigateurs : cartes Portolani
-
Peintres : vers la perspective
Pour le praticien : Chercher à se démarquer des autres, en particulier en s'attaquant à des problèmes issus des nouvelles représentations.
-
-
Uniformisation et homogénéisation : Ce qui permet de mesurer
-
Le temps : l'heure (1270) et la musique (les temps (le rythme) et les silences)
-
Le travail : la monnaie
-
L'espace :
-
le plein et le vide
-
espace astronomique devenant infini, homogénéisation de l'espace astronomique
-
Le nombre, par l'intermédiaire d'une unité de mesure, est un outil de représentation qui dynamise le questionnement.
À la fin du Moyen Âge, le visuel et le quantitatif sont de plus en plus utilisés. Le terrain se prépare pour l'algèbre.
-
Qui sont les abaquistes ?
- Commerce international à partir de Venise, Gênes, Pise, Florence.
- D'aborde des succursales jusqu'à la grande peste noire (1348). La population de l'Europe diminue de moitié. Faillites des grandes compagnies.
- Développement par la suite des compagnies
à filiales, indépendantes de la maison mère.
Exemple : Les Médicis (après 1450), dpuis Florence, avec filiales à Londres, Bruges, Lyon, Rome, Milan, Avignon.
- Début de la comptabilité à double entrée.
- Les écoles de marchands :
- de 7 à 10 ans : école de lecture, écriture et grammaire
- après 10 ans : apprentissage de l'abaque et des algorithmes
- En 1338, à Florence (env. 1000 000 habitants), 6 écoles pour un totoal de 1000 à 2000 élèves.
- Les propriétaires de ces écoles sont parmi les plus riche de la classe moyenne.
- Que font-ils en algèbre ?
- Le livre Kadran aux marchans, (Voir les exemples ci-dessous)
- Ces livres contiennent des problèmes pratiques, mais à mesure de plus en plus de problèmes artificiels de nature algébrique, mais sans théorie.
- Multiplication des règles
- Dardi de Pise (v. 1350) en a 198
- Benedetto de Florence (v. 1460) en a 36.
- Difficile de savoir si une méthode est générale (voir le cas de Biagio il Vecchio, v. 1330), Voir les exemples ci-dessous. Sa méthode a été crue juste pendant 150 ans.
- Difficulté de bien choisir les inconnues. On peut choisir une inconnue menant à une équation difficile à résoudre. Difficulté de manipuler plusieurs inconnues simultanément
- Mais les règles mênent parfois à des choix surprenant : de 'Mazzinghi (v. 1370) passe par des nombres négatifs pour trouver une solution positive.
-
Exemples tirés de livres d'abaquistes
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |