École pythagoricienne : Tout est nombre (vers -500)
Pythagore de Samos (582 - 497 av. J.C.)[1], élève d’Anaximandre et peut-être même de Thalès, marqua profondément la pensée grecque, et, après elle, la pensée occidentale. Pourtant, il est loin d’être un démocrate. Après avoir quitté les côtes de la mer Égée, il s’installe à Crotone, au sud de l’Italie, où il fonde une secte qui s’entoure de mystères. La secte prenant parti pour les aristocrates et contre les démocrates, elle est chassée de Crotone avec son chef vers 510 av. J.C.. Elle est par la suite l’objet de persécutions et disparaît complètement comme entité politico-religieuse vers 350 av. J.C.Cosmologie : esthétisme, Zeus au centre de l'univers.
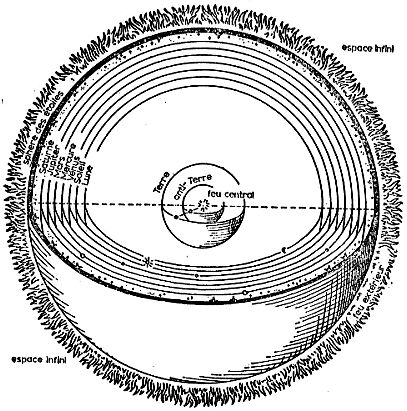
Système de Philolaos (-480, ?)
Comme pour Anaximandre, la pensée des pythagoriciens donne une importance fondamentale à la symétrie et plus généralement à l’esthétisme. Dans cette cosmologie, le principe de la symétrie est plus poussé que chez Anaximandre. Tout est organisé symétriquement autour du centre de l’univers. Il n’y a ni haut ni bas. Tout repose sur la figure parfaite par excellence, la sphère. La Terre elle-même est vue comme une sphère placée au centre de l’univers. Au centre de cette sphère brûle le feu central, résidence de Zeus, le premier parmi les dieux. Les planètes tournent autour de la Terre. Elles sont placées sur des sphères concentriques. La sphère extérieure est celle des étoiles. Au-delà brûle le feu extérieur. Dans la cosmologie des premiers pythagoriciens, les sphères émettent des sons qui sont en harmonie les uns avec les autres. La légende veut que seul Pythagore pût entendre cette musique des sphères. Ainsi il pouvait non seulement percevoir l’esthétisme géométrique de l’univers, mais aussi associer ce dernier à un esthétisme sonore, musical. Il y a là un message : lorsque perçus sous un certain angle, des phénomènes sans liens apparents peuvent de fait présenter des analogies. C’est le devoir du pythagoricien de rechercher ces analogies secrètes qui dévoilent la vraie nature de l’univers. Le nombre est l’outil fondamental qui permet de mettre en évidence ces analogies. C’est pourquoi, pour un pythagoricien, «tout est nombre». (N.B. Le «nombre» doit être compris ici comme un nombre naturel ou rapport de nombres naturels. De tels rapports sont ce que nous appelons aujourd'hui des nombres rationnels.)
Tout est nombre : musique, arithmétique, astronomie, médecine.
Le nombre apparaît en musique par le biais des cordes vibrantes. Le son émis par une corde tendue qui vibre est fonction de la longueur de la corde. Les pythagoriciens remarquèrent que, lorsque deux cordes ont des longueurs qui sont dans un rapport simple, leurs sons respectifs sont harmonieux pour l’oreille. Ainsi, le rapport de 2 à 1 des longueurs correspond en musique à un intervalle d’une octave, le rapport de 3 à 2 correspond à une quinte et celui de 4 à 3 à une quarte. La musique des sphères devrait aussi se ramener à des rapports simples.
Les figures elles-mêmes sont caractérisées numériquement. Ainsi les triangles sont associés à la suite des nombres 3, 6, 10, etc., appelés nombres triangulaires. Un coup d’oeil à la figure ci-dessous nous fait voir pourquoi. De même, la suite des nombres 4, 9, 16, etc. est associée au carré.
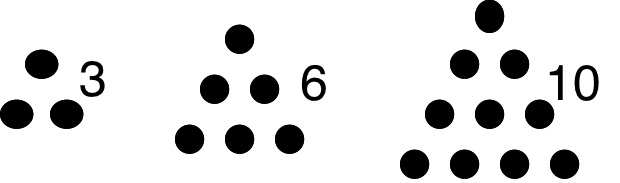

Les pythagoriciens ont ainsi développé une théorie des nombres figurés. Cette théorie est toutefois plus qu’une curiosité. Il semble que ce soit dans le cadre de celle-ci que furent faites les premières démonstrations mathématiques. Voyons un exemple. L’énoncé: Tout nombre carré est la somme de deux nombres triangulaires consécutifs. Un simple coup d’oeil sur la figure ci-dessous nous permet de nous rendre compte de la véracité de cet énoncé dans le cas du nombre carré 16 qui est la somme des nombres triangulaires 6 et 10. Mais il permet de voir qu’il est facile de généraliser le raisonnement à quelque nombre carré que ce soit.
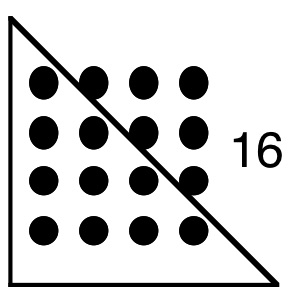
Il y a même des liens entre ces nombres figurés et la musique. Ainsi, les premiers nombres rectangulaires, 2, 6, 12 ont une correspondance avec les rapports consonants simples, car 2 est associé au rapport de 2 à 1, l’octave, 6 est associé au rapport de 3 à 2, la quinte, 12 est associé au rapport de 4 à 3, la quarte. [2]
Le vocabulaire pythagoricien aujourd'hui.
Plusieurs termes que nous utilisons aujourd’hui sont d’origine pythagoricienne. Ainsi en est-il du terme tonus. Il fut appliqué au corps lorsque les pythagoriciens établirent des analogies entre l’harmonie musicale et l’harmonie du corps. Un corps sain est un corps dont les différentes parties sont en harmonie les unes avec les autres. En musique, une pièce est habituellement écrite dans un certain ton, autrement dit dans une certaine gamme. Être dans le ton implique d’être en harmonie avec la pièce. Un corps qui a du tonus est un corps dont les différentes parties sont dans le ton les unes avec les autres. C’est un corps sain.
L’on pourrait établir des filiations similaires pour les mots tempérament et tonique. Pas surprenant que l’on croyait aux propriétés thérapeutiques de la musique.
Le mot anglais «figure», qui signifie chiffre, est aussi d’origine pythagoricienne. Il exprime simplement le lien entre les nombres et les figures géométriques discrètes.
Un autre mot d’usage courant mérite que l’on s’y arrête. Il s’agit du mot «théorie». Voici les explications données par Koestler (p. 33):
Extase et connaissances : Savons-nous encore les associer avec une telle ferveur?
L’extase provoquée par la découverte des analogies numériques entre des phénomènes en apparence différents constitue une première. En effet, pour la première fois, la recherche d’explications passe par la mesure. Associer un nombre à une grandeur devient un processus nécessaire pour pouvoir mettre en évidence les analogies cachées. Pour les pythagoriciens, l’explication d’un phénomène passe par l’arithmétique. Les rapports numériques et les proportions sont au coeur du discours explicatif.
La fin d’un rêve : Tout n’est pas nombre.
La secte des pythagoriciens fut chassée de Crotone par le parti démocratique. Elle se répandit dans tout le monde grec. Cet exil forcé eut un côté positif puisque les idées de la secte furent connues dans tout le bassin méditerranéen. Politiquement, elle disparaît vers 350 av. J.C. Cette disparition ne découle pas simplement d’actions politiques. Elle trouve aussi sa source dans une découverte qui vint saper les bases mêmes de leur système : «Tout n’est pas nombre».
Affirmer que «Tout est nombre» implique non seulement que tout est mesurable, mais aussi que des grandeurs de même nature peuvent être mises en rapport les unes avec les autres en comparant leurs mesures.
Prenons deux segments A et B comme exemple. Pour chacun de ces segments, je peux trouver des unités de mesure telles que, si je les mesure par rapport à ces unités, les segments auront chacun une mesure entière. Une règle d’un mètre mesure 1 si l’unité de mesure est le mètre. Elle mesure 100 si l’unité de mesure est le centimètre. Etc. Par ailleurs, si j’utilise le pouce comme unité de mesure, la règle n’aura pas de mesure entière. Pour les pythagoriciens, mesurer la règle d’un mètre en employant le pouce ne présente aucun intérêt. Il leur faut utiliser des mesures qui sont entières et donc choisir une unité de mesure en conséquence. Cela ne présente habituellement aucune difficulté. Cependant, lorsqu’il s’agit de comparer deux segments l’un à l’autre, le problème se complique. Les pythagoriciens croyaient qu’il était toujours possible de trouver une unité de mesure qui mesurerait exactement deux segments, c’est-à-dire qui entrerait un nombre exact de fois dans chacun des segments. Ainsi, le rapport de deux longueurs pourrait toujours s’exprimer comme rapport de deux nombres entiers. Or voici qu’un membre de la secte découvrit qu’il est impossible de trouver une unité de mesure qui mesure exactement à la fois le côté d’un carré et sa diagonale. Ces deux segments sont donc incommensurables. Pour les pythagoriciens, cette découverte est tragique. Le sol se dérobe sous leurs pieds.
La découverte de l’existence de segments incommensurables constitue non seulement un véritable cataclysme dans la secte, elle provoque la séparation complète de l’arithmétique et de la géométrie. Les Grecs n’arriveront jamais à transcender cette brisure. Certes l’arithmétique est comprise dans la géométrie (prendre tous les segments commensurables à un segment donné). Mais la découverte d’une paire de segments incommensurables montre que la géométrie a un domaine d'application plus large que celui de l'arithmétique. Aussi, à la suite de la chute des pythagoriciens, l’arithmétique prendra une forme purement géométrique chez les philosophes et les mathématiciens. L’arithmétique telle que pratiquée par les marchands sera vue quant à elle comme un domaine sans statut intellectuel, d’autant plus que les marchands étaient plutôt au bas de la hiérarchie sociale. La séparation entre la géométrie et l’arithmétique devint irréversible lorsque Zénon d’Élée énonça ses paradoxes (Achille et la Tortue, la Dichotomie). Ces paradoxes montraient l’incapacité de notre pensée à mener avec assurance des raisonnements impliquant l’infini. Or, pour établir une relation de type numérique entre la diagonale d’un carré et l’un de ses côtés, il faut faire appel à un processus infini. Les Grecs se trouvent ainsi piégés. La géométrie fera des progrès remarquables. L’usage des nombres deviendra marginal en géométrie. La mesure des grandeurs sera reléguée au second plan pour près de 1800 ans.
Un ingénieur : Eupalinos et le tunnel de Samos.
Pour montrer les capacités remarquables des Grecs en ingénierie, voyons l’exemple d’un contemporain de Pythagore qui vécut aussi à Samos au temps où Pythagore y habitait encore.
Selon le grand historien grec Hérodote, Eupalinos est un ingénieur qui creusa un long tunnel destiné à amener l’eau jusqu’à la ville de Samos. Mais la localisation précise du tunnel avait été oubliée et plusieurs pensaient même qu’Hérodote avait inventé son existence ou avait simplement repris une légende. Toutefois, au début de ce siècle, le tunnel fut redécouvert. Long de plus de 900 mètres, il a été creusé par les deux bouts simultanément. Les équipes se sont rejointes à mi-chemin n’ayant dévié l’une de l’autre que d’un mètre environ. Hérodote avait raison. Il s’agit bien d’une merveille de l’ingénierie.
Extension de la cosmologie pythagoricienne : Philolaos (-480, ?), Héraclide (-388, -315), Aristarque (-320, -250)
La cosmographie pythagoricienne telle que vue par l’astronome Philolaos (-480, ?) s’inspire de la cosmologie pythagoricienne primitive. (Son sytème est illustré au haut de la page) Toutefois, la Terre, une sphère, n’est plus au centre de l’univers. Le principe de symétrie est-il ici mis de côté? Non. De fait, comme nous l’avons souvent répété, pour les pythagoriciens tout est nombre (entendre nombre naturel). Or, dans la mystique des nombres qu’élaborent les pythagoriciens, le nombre 10 est fondamental. Il est le troisième nombre triangulaire. Il devrait donc se retrouver dans la structure de l’univers. Philolaos suggère que l’univers soit composé de 10 sphères. L’on ne connaissait alors que 7 corps mobiles : Lune, Soleil, Mercure, Vénus, Mars, Jupiter et Saturne. Avec la sphère des étoiles, cela fait 8 sphères, en supposant que l'orbite de chaque planète se situe sur une sphère dont le centre est aussi le centre de l’univers. Il faut donc ajouter deux autres sphères pour en avoir 10. Aussi, la Terre doit quitter le centre de l'univers et être placée sur une sphère. Entre la Terre et le centre de l’univers, une autre sphère vient s’ajouter, la sphère de l’Anti-terre. Le centre de l’univers est occupé comme auparavant par le feu central, résidence de Zeus, à ne pas confondre avec le Soleil. L’Anti-terre a la particularité d’être toujours placée exactement entre la Terre et le feu central de sorte que, de la Terre, ce dernier n’est jamais visible.
L’astronome Héraclide, élève de Platon et donc postérieur à l’époque des pythagoriciens, reprendra l’idée pythagoricienne de voir la Terre comme une sphère. Il la situe à nouveau au centre de l’univers, le feu central ayant réintégré le centre de la Terre. Cependant, au lieu de faire tourner les sphères dans un mouvement de rotation de 24 heures, il fait tourner la Terre elle-même. Autre différence, les planètes tournent autour d’elle sauf pour Mercure et Vénus qui tournent autour du Soleil.
La combinaison des idées de Philolaos et d’Héraclide ouvre de nouvelles possibilités d’organisation du système planétaire. Aristarque explora ces nouvelles possibilités. Il en vint à proposer un système héliocentrique globalement similaire à celui proposé 1800 ans plus tard par Copernic. Malheureusement, Aristarque ne fit pas école. Ses idées furent plus ou moins oubliées jusqu’à ce que les astronomes de la Renaissance les dépoussièrent.
______________________
[1] Tous les auteurs ne s’entendent pas sur les détails de la vie de Pythagore. Certains vont même jusqu’à dire que Pythagore n’est pas un personnage historique et que seule la secte religieuse a vraiment existé.
[2] Voir Koestler, Arthur, Les somnambules, Essai sur l’histoire des conceptions de l’Univers, Calmann-Lévy, 1960, p. 26.
