École ionienne : Thalès de Milet (-624, -546)
La légende veut que Thalès de Milet fut introduit aux secrets de l’univers par les prêtres égyptiens et les mages babyloniens. L’historien grec Hérodote raconte, 150 ans après l’époque de Thalès, que ce dernier avait prédit l’année au cours de laquelle une éclipse totale du soleil devait se produire. Lorsque l’éclipse se produisit effectivement comme prévu, les Grecs furent remplis d’admiration pour Thalès. Toutefois, sachant que Thalès avait voyagé en Mésopotamie et que les Babyloniens avaient développé une méthode pour prévoir les éclipses à une année près, nous pouvons penser que le philosophe grec n’a fait qu’appliquer ce qu’il avait appris au cours de ses voyages. On attribua à Thalès les premières tentatives d’explication des phénomènes naturels sans se référer aux dieux. Il passa ainsi progressivement du mythe à la science.Cosmologie. L'élément fondamental : l'eau
La cosmologie de Thalès repose sur l’idée que l’eau constitue l’élément fondamental de l’univers. La Terre repose sur une masse d’eau qui, comme chez les Égyptiens et les Babyloniens, l’entoure de toute part. Les planètes sont ici aussi des barques, mais des barques qui suivent un trajet immuable, des barques qui n’ont rien à voir avec les dieux. L’eau est à la base de l’univers d’un autre point de vue. Toute matière est constituée d’eau. Le feu et l’air sont de l’eau évaporée. Les solides sont de l’eau condensée. L’eau céleste provient de la condensation de l’eau qui émane de la terre.
Les mathématiques : au-delà de ce qui est accessible
Plus intéressant encore est le travail de Thalès en géométrie. La légende veut que, lors de son séjour en Égypte, on lui ait demandé de mesurer la hauteur d’une pyramide. Sans même monter sur la pyramide, Thalès s’exécuta. Sa méthode est fort ingénieuse. Elle consiste à mesurer l’ombre faite par un bâton et celle faite par la pyramide. Si l’ombre de la pyramide est 50 fois plus grande que celle du bâton, alors la pyramide est 50 fois plus haute que le bâton.
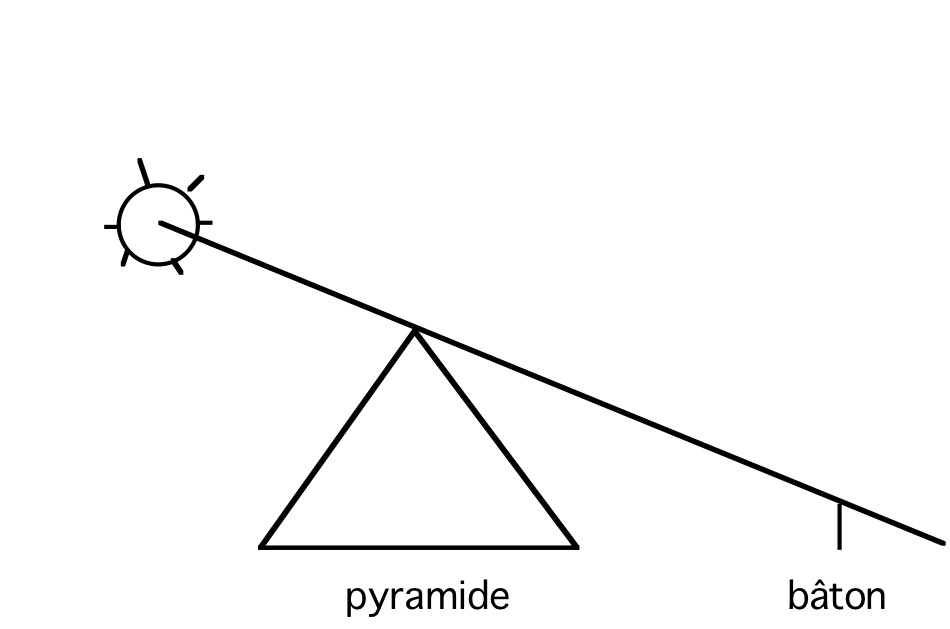
Cet usage de la proportionnalité est important à plusieurs égards. En premier lieu, elle illustre comment l'inaccessible peut devenir accessible. Plus précisément, il devient possible, par de tels raisonnements, de connaître sans avoir besoin du toucher, et cela tout en gardant un haut degré de certitude. Cette constatation peut nous paraître banale. Dans le monde antique, et particulièrement dans le monde grec, elle tient d’une véritable révélation. Pour les Grecs, l'homme entre en contact avec la nature par le moyen de ses sens. Or peut-on vraiment faire confiance à nos sens? Les illusions d’optique nous montrent assez bien que la vue nous trompe souvent. On ne peut davantage être certain de l’ouïe et encore moins du goûter, sans parler de l’odorat. Alors le seul sens fiable semble être le toucher. Nous verrons qu’Aristote base son explication du mouvement sur le toucher. Dès lors, le fait d’utiliser un raisonnement qui assure un degré de certitude équivalent à celui du toucher constitue une première brèche dans cette croyance voulant que le toucher soit le sens le plus sûr. La déduction se montre ici de fait plus efficace que le toucher. Cet enseignement ne tombera pas dans des oreilles de sourds.
Pensée inductive et pensée déductive
La pensée inductive va du particulier au général. De quelques observations, elle induit des règles générales. Exemple: Les quatre premiers étudiants qui entrent dans la classe ont les cheveux roux; j’en déduis que tous les étudiants qui entreront par la suite auront les cheveux roux. L’on constate ici l’importance de multiplier les observations. Mais même lorsque le nombre d’observations est très grand, on ne peut être assuré que le principe général qui se dégage soit toujours vrai. La pensée déductive va du général au particulier. Ainsi, la loi de la gravitation de Newton se veut générale. Dès lors, je peux l’appliquer au mouvement d’un corps céleste particulier, un satellite par exemple. Exemple: dans la cosmographie d’Anaximèdre (-610, -546), un disciple de Thalès, le principe général est que la symétrie est importante et a une valeur d'explication. En conséquence, la Terre doit être au centre de l’univers, car elle doit satisfaire le principe de symétrie. Si l’on constate que la Terre n’est pas effectivement au centre de l’univers, il faudrait alors renoncer au principe de symétrie comme principe universel.
Vers la démocratie (vers -500) : fin des mythes, importance de l'Agora pour le développement de l'idée de preuve (rhétorique et dialectique).
Vers 500 av. J.C., le régime politique des cités-États grecques se modifie. La démocratie [1] s'installe progressivement dans plusieurs cités. Certaines cités demeurent fidèles à la royauté. D’autres tombent sous la coupe de tyrans. Mais, néanmoins, les idées démocratiques s’infiltrent un peu partout. La diversité des régimes politiques assure la survie de plusieurs systèmes philosophiques. Le dynamisme engendré par l’existence simultanée de ces systèmes est nourri par la dynamique intrinsèque à l’activité démocratique. En effet, pour recevoir le support des électeurs, le candidat à un poste électif doit convaincre ses électeurs que ses idées sont les plus aptes à lui permettre de bien remplir ses fonctions. Au fond, ce que le candidat propose à ses électeurs, ce sont des principes généraux qui, une fois appliqués, se montreront bénéfiques pour le bien commun. Pour convaincre les électeurs, il doit développer une argumentation que ses adversaires ne sauront pas attaquer avec succès. La structure logique devient donc très importante. Elle devient le support du discours. La démocratie amène la fin de la dictature des mythes. La conviction n’est plus donnée a priori. Elle découle d’une démonstration qui prend une forme discursive.
Les Grecs attribuèrent une grande importance aux discussions publiques. Ainsi, l’agora, la place du marché, devient dans une ville le lieu privilégié pour les grands débats. Raisonnements déductifs, démonstrations, logique. Qui penserait qu’ils se sont développés parmi les poules et les étals des bouchers?
______________________
[1] En fait cette démocratie est limitée à une classe supérieure. Les marchands par exemple ne font pas partie de cette classe. Il en va bien sûr de même pour les esclaves. (Voir Ben-David)
