Atteindre l'inaccessible : Les mathématiques dans l'histoire

L'univers : une machine

Galilée (1564-1642)

Caractéristiques du nouveau style scientifique :

    • Mesures quantitatives et donc importance des instruments de mesure
    • Contrôle des variables :
        Ceteris paribus ,
        Répétition un grand nombre de fois d’une même expérience,
        Description précise des expériences pour qu’elles puissent être reprises à volonté.
    • Expériences planifiées (elles ont un ou des buts prédéterminés)
    • Les lois sont descriptives et ne sont pas “explicatives”.

(Par exemple, la loi de la chute des corps : le rapport des distances parcourues par un corps en chute libre est proportionnel aux carrés des temps de la chute)

On peut résumer la méthode expérimentale de Galilée par le diagramme suivant :

 

L’approche de Galilée se démarque de celles des traditions organique et mystique (magique). Certes l’importance de la mesure rappelle l’importance des nombres dans la tradition magique. Toutefois, Galilée ne cherche pas à aller au-delà de la description des relations numériques entre les variables numériques qui permettent une description numérique du phénomène. Il accepte ces relations pour ce qu'elles sont: une description. Il regarde les phénomènes comme un ingénieur regarde une machine fonctionner. Il est un digne successeur d’Archimède. C’est pourquoi la nouvelle tradition qui émerge est appelée la tradition mécanique.

Descartes (1596-1650) : les besoins d'une méthode en ce XVII^e siècle

Pourquoi tant de « méthodes » au XVII^e siècle ?

Extrait du Discours de la méthode  (1637) :

Le premier était de ne recevoir jamais aucune chose pour vraie, que je ne la connus évidemment être telle : c’est-à-dire, d’éviter soigneusement la précipitation et la prévention; et de ne comprendre rien de plus en mes jugements, que ce qui se présenterait si clairement et si distinctement à mon esprit, que je n’eusse aucune occasion de le mettre en doute.

Le second, de diviser chacune des difficultés que j’examinerais, en autant de parcelles qu’il se pourrait, et qu’il serait requis pour les mieux résoudre.

Le troisième, de conduire par ordre mes pensées, en commençant par les objets les plus simples et les plus aisés à connaître, pour monter peu à peu, comme par degrés, jusques à la connaissance des plus composés; et supposant même de l’ordre entre ceux qui ne se précèdent point naturellement les uns les autres.

Et le dernier, de faire partout des dénombrements si entiers, et des revues si générales, que je fusse assuré de ne rien omettre.

Remarquons la tendance à ordonner les connaissances pour les intégrer dans une structure de type axiomatique. Le besoin de diviser les problèmes pour mieux les étudier pointe par ailleurs vers une spécialisation progressive de la recherche.

Importance des mathématiques et explications mécaniques (Principia  Philosophiæ  (1644))

La méthode expérimentale de Descartes reprend celle de Galilée, mais avec une plus grande importance donnée à la modélisation mathématique et une conscience plus explicite du rôle des mathématiques dans la production de prédictions qui seront à vérifier expérimentalement.

Descartes voit le monde comme une immense machine. De ce fait, il accepte mal l’idée mise de l’avant par Kepler qu’il y a des actions à distance. Il revient à la position grecque voulant que les actions se fassent par contact. Dès lors, il reprend l’affirmation d’Aristote que le vide n’existe pas. Dans cette voie, il édifie une théorie dite des tourbillons qui tente d’expliquer mécaniquement le mouvement des planètes par la combinaison de tourbillons de matière subtile interplanétaire. Descartes se démarque de Galilée dans le sens que, contrairement à ce dernier, il ne se satisfait pas toujours d’un modèle mathématique. Il a des relents d’aristotélisme en cherchant à remonter à des causes premières, comme avec les tourbillons.  Il faut dire que dans sa théorie des tourbillons Descartes ne donne pas aux mathématiques la place qu’il annonce, dans ses écrits sur la méthodologie, devoir lui réserver.

Newton (1643 (42) -1727) : l'« explication » de la nouvelle vision de l'univers de Kepler et Galilée

La méthode de Newton reprend dans les grandes lignes celle de Galilée. Toutefois, Newton subit l’influence de Descartes. Le rôle des mathématiques y est encore plus accentué. Il raffine aussi l’interaction entre la théorie et les expériences visant à vérifier les prédictions de la théorie.

Le tableau suivant schématise la méthode de Newton.

 

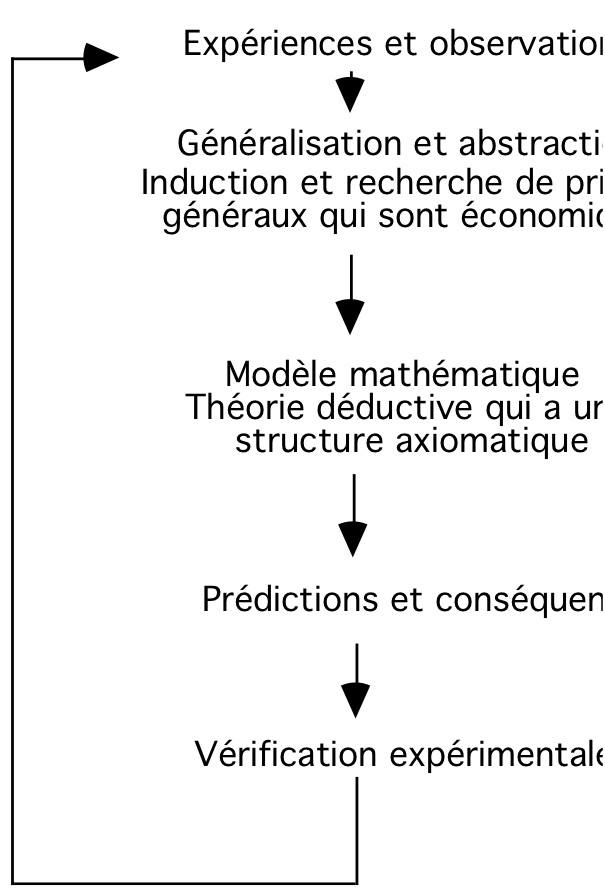
Généralisation et abstraction :
Newton cherche à aller bien au-delà des apparences. Il veut construire un modèle qui soit économique, c’est-à-dire qui repose sur un petit nombre d’énoncés desquels il sera possible de déduire les propriétés du modèle. En édifiant sa théorie de la gravitation, Newton isole quelques variables qui lui sont apparues importantes à la suite d’observations et d’expériences et qui lui paraissent pouvoir jouer un rôle central dans un modèle mathématique. Il joue mathématiquement avec elles afin d’étudier les différentes façons d’établir des relations entre elles. Il peut alors pressentir la structure du modèle le plus économique. C’est au cours de cette étape que Newton a compris l’importance de l’inertie qui pourtant n’est pas quelque chose qui se voit. C’est aussi au cours de cette étape, étudiant les calculs de Kepler, que Newton a perçu le lien mathématique entre la troisième loi de Kepler (le carré de la période de révolution d’une planète est proportionnel au cube du grand axe de son orbite) et la loi de la gravitation universelle.

Newton et les trois traditions

Newton est clairement un adepte de la tradition mécanique. Les modèles qu’il privilégie sont des modèles mathématiques dans lesquels les causes premières sont absentes. Par exemple, dans son Principa Mathematica, Newton est conscient qu’il ne peut connaître la nature de la force de gravitation.

La vision mécanique de Newton va plus loin que celle de Galilée. En effet, elle recherche la forme la plus économique possible, le mot économique étant pris au sens de minimiser le nombre de lois fondamentales et d’axiomes sur lesquels repose le modèle. Les mathématiques sont avant tout le langage des modèles et non pas celui de la nature. Au fond, nous ne connaissons pas la nature, mais seulement les modèles qui nous permettent de prévoir certains de ses comportements. De ce point de vue, Newton est, jusqu’à un certain point de vue, un platonicien. La seule connaissance accessible aux hommes est celle des modèles, modèles qui n’existent pas dans la nature, dans le monde réel. Ces modèles, idéalement mathématiques, ne participent-ils pas aux Idées de Platon?

Mais Newton n’est pas un platonicien pur. Ses modèles sont le fruit des observations et des expériences. Les êtres abstraits qui constituent les modèles sont le fruit du travail des hommes. Voilà une perception très aristotélicienne du monde. D’ailleurs, la structure même des Principia Mathematica, avec ses définitions, axiomes, propositions, est celle proposée par Aristote deux mille ans plus tôt.

Newton est donc véritablement un grand amphibien. Il est à l’aise partout, car il a su dépasser les frontières qui séparaient les trois traditions auxquelles il s’est abreuvé. Avec Newton, la science change profondément. Après lui, rien ne sera plus pareil.