Applications de e dans divers domaines
Bien que le nombre e ne soit pas aussi populaire que π ou encore le nombre d’or, il est utile dans plusieurs domaines, la plupart du temps en lien avec les sciences. Il n’y a pas un très grand nombre d’applications où notre fameux nombre est utile, mais il reste indispensable en physique, en électricité et en électronique.
Loi de la désintégration
En physique nucléaire, le nombre e est utilisé afin de calculer le temps de demi-vie d’un ensemble d’éléments, aussi appelé période radioactive, par la formule suivante :
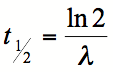
Le nombre e se retrouve dans le logarithme naturel utilisé, qui est donc de base e. La demi-vie (
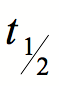) de l’ensemble étudié se calcule en fonction du taux de croissance (
).
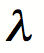Ce taux tient compte uniquement de l’élément et du mode de
désintégration en question, les conditions d’environnement ne changent
donc rien à ce processus. Il ne faut pas penser qu’après deux temps de
demi-vie la période radioactive sera terminée, elle sera rendue à 25%
de son activité initiale. En effet, après une demi-vie on en sera à 50%
et le deuxième temps réduira de moitié ce qui reste de radioactivité,
ce qui nous porte à 25%.Pour en savoir plus : Wikipédia : loi de désintégration radioactive
Charge et décharge d’un condensateur
En physique électrique, la charge et la décharge d’un condensateur par une résistance sont utilisées en électronique. De manière générale, elles servent à créer une sorte de délai pour retarder le départ ou l’arrêt de l’engin auquel le circuit est branché. Elles obéissent à la formule suivante :
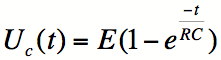
où U est la différence de potentiel en fonction du temps t, E la tension à la source, R la résistance et C la capacité du condensateur.
Réseau de neurones artificiels
Bien que les fonctions contenant le nombre e puissent prendre une infinité de forme, la fonction sigmoïde, dont l’équation est
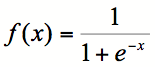demeure
bien utile dans plusieurs cas. En effet, cette fonction est nécessaire
dans le fonctionnement de réseaux de neurones, qui eux sont exploités
dans
plusieurs domaines. En autre, on les utilise dans la classification
d’espèces animales selon une
analyse d’ADN, dans la reconnaissance optique de caractères, comme pour
les billets de banque dans un guichet automatique, ou encore à des fins
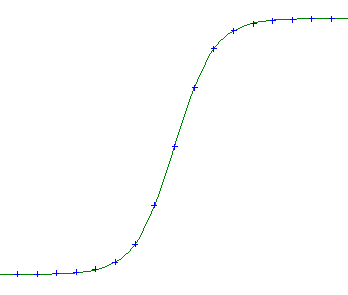
d'estimations boursières. Le graphique de la courbe de la fonction sigmoïde est :
Intérêts composés
Le domaine par lequel il est le plus facile d’introduire le nombre e est sans contredit en finance à partir de la notion d’intérêts composés. Effectivement, c’est souvent de cette manière que les enseignants du secondaire amènent le nombre e aux élèves de cinquième secondaire. Pour un placement initial de a dollars, à un pourcentage d’intérêt annuel i, si les intérêts sont composés de manière continue, il est possible de calculer le montant p du placement après r années avec l’équation suivante :
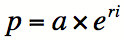
Puisque e est la limite de la formule d’intérêts composés lorsque n (le nombre de compositions) tend vers l’infini :
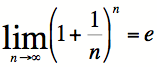
Dans la vie réelle, aucune institution bancaire n’offrirait une telle occasion d’augmenter notre compte en banque, mais les intérêts composés sont une notion vue en cinquième secondaire et l’équation présentée précédemment reste un bon moyen de voir qu’il y a une limite à la composition d’intérêts.
Voir l'activité sur les intérêts composés pour plus de détails.