Image de efond

Le nombre e au niveau collégial


Dans l’enseignement au Québec, le nombre e est d’abord introduit au secondaire par le biais des fonctions exponentielles et logarithmiques. Par ailleurs, la connaissance de ce nombre est davantage nécessaire au niveau collégial. Dans les cours du cégep où on traite le calcul différentiel et intégral, on exploite notamment le concept de limite qui a été nécessaire à Bernouilli pour définir le nombre e. De plus, on applique de nouvelles opérations nommées différenciation et intégration à une fonction qui implique directement le nombre e,
 e^x .

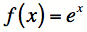Comme ce site a été crée pour une clientèle dont le niveau mathématique est celui du secondaire, on propose ici une vulgarisation de ces concepts rédigée par Peter J. Bentley dans son Livre des nombres. Celle-ci explique merveilleusement bien les concepts de dérivées et d’intégrales à un public pour qui le détail de ces opérations est inconnu.

" Jacob aime beaucoup le vélo de montagne. Avant de partir en randonnée, il analyse la carte qui présente la forme de la colline à escalader. Il doit toutefois déterminer si à certains endroits, la pente sera trop escarpée pour pouvoir en venir à bout à vélo. Jacob doit donc calculer le dénivelé de la courbe de la colline avant d’entreprendre son excursion. On suppose que la courbe de la colline est décrite par l’équation suivante :
 col2,
où y est la hauteur de la colline et x la distance horizontale sur le sol. En procédant à la différenciation de cette équation, on obtient une nouvelle équation :
col3,
qui indique pour chaque endroit sur la colline, défini par un couple de coordonnées x et y, la pente en cet endroit de la colline. Jacob peut donc vérifier pour les endroits les plus escarpés de la colline sur la carte que la valeur de la pente n’est pas trop élevée pour escalader la colline à vélo. Par ailleurs, l’intégration fonctionne exactement de manière inverse. Si on connaît le dénivelé d’une colline, il est possible de déterminer sa forme, et plus précisément l’aire sous la courbe de cette colline. "

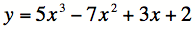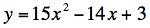Ainsi, il existe un bon nombre de règles de calcul qui permettent d’effectuer la différenciation ou l’intégration d’une équation, selon le type d’équation dont il s’agit (polynomiale, sinusoïdale, rationnelle, exponentielle, etc.). Ces règles font l’objet de deux cours de niveau collégial, chacun portant principalement sur l’une de ces deux opérations.

Ce vers quoi on voulait attirer votre attention est que la fonction exponentielle 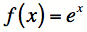e^x est la seule* fonction pour laquelle la différenciation et l’intégration n’ont aucun effet!  Cela confère donc à cette fonction un statut très particulier : celle-ci n’exige aucun calcul dans la branche des mathématiques que constitue le calcul différentiel et intégral. Voilà qui s’avère fort utile pour les mathématiciens !



* Note : La fonction 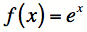col1 est un cas particulier de la famille de fonction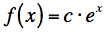col4, où la valeur de c est 1. Cette famille de fonctions n'est pas affectée non plus par les procédés de différenciation et d'intégration. 



Bibliographie
  • BENTLEY, Peter J. Livre des nombres, Sélection du Reader’s Digest (Canada), Montréal, 2008.
  • CHARRON, Gilles; PARENT, Pierre. Calcul différentiel, 5e édition, Éditions Études Vivantes, Laval, 2002.
  • CHARRON, Gilles; PARENT, Pierre. Calcul intégral, 3e édition, Éditions Études Vivantes, Laval, 2004.