Histoire de la découverte du nombre e
L’invention des logarithmes
L’histoire du nombre e débute en Suisse, grâce aux travaux de John Napier (ou Neper, selon les traductions, dont le portrait est présenté ci-dessous). Fort de ses études à la St-Andrews University, il consacre une bonne partie de sa vie à la gestion et à l’administration de ses terres. Les mathématiques le fascinent particulièrement et en 1614, il publie un manifeste qui lui prit près de vingt ans à rédiger,
 le Mirifici logarithorum canonis descriptio.
Cet ouvrage a un but précis : simplifier le travail de tous les
hommes qui ont des calculs à effectuer dans l’exercice de leur métier,
donc permettre à tous ces calculateurs d’alléger leurs tâches quotidiennes. Ce qui embête le plus ces hommes, il l’énonce lui-même :
le Mirifici logarithorum canonis descriptio.
Cet ouvrage a un but précis : simplifier le travail de tous les
hommes qui ont des calculs à effectuer dans l’exercice de leur métier,
donc permettre à tous ces calculateurs d’alléger leurs tâches quotidiennes. Ce qui embête le plus ces hommes, il l’énonce lui-même : « (…) il n’existe rien (à juste titre, chers étudiants en mathématiques) d’aussi fastidieux dans la pratiques des mathématiques, et qui gêne et empêche autant le travail des calculateurs que les multiplications, les divisions, l’extraction de racines carrées et cubiques de nombres immenses, qui en outre prennent du temps et sont sujettes à d’innombrables fautes d’inattention (…) »
Ainsi, Napier invente les logarithmes, qui ont pour objectif de substituer aux multiplications et aux divisions, des additions et des soustractions. Voici donc un exemple de l’utilité de cet outil innovateur, qui rappelons-le à l’époque, était d’une efficacité incontestée compte tenue que la calculatrice n’existait pas encore.
On définit le logarithme tel que
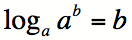 .
. Le logarithme est donc l’exposant qu’il faut affecter à la base a pour obtenir le nombre
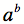 .
. Si on prend un exemple numérique,
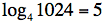 ,
cela signifie que 5 est l’exposant qu’il faut affecter à la base 4 pour
obtenir le nombre 1024. En quoi cela simplifie-t-il les calculs vous
demandez-vous ?
,
cela signifie que 5 est l’exposant qu’il faut affecter à la base 4 pour
obtenir le nombre 1024. En quoi cela simplifie-t-il les calculs vous
demandez-vous ? La pertinence de l’outil qu’est le logarithme résulte des lois des logarithmes qui s’y rattachent. Ainsi, on transforme un produit par une somme tel que :
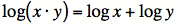
Note : Lorsque la base n’est pas indiquée, on prend pour acquis que celle-ci est 10.
Par conséquent, si un calculateur du XVIIe siècle désire effectuer une multiplication de deux nombres, prenons par exemple 78 et 56, il n’a qu’à appliquer la loi des logarithmes ci-dessus pour simplifier ses calculs et à utiliser les tables des logarithmes de Napier.
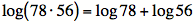
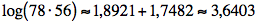
Comme les logarithmes ont une fonction purement calculatoire, ils sont souvent appelés « nombres artificiels ». Ainsi, grâce aux tables de logarithmes et à la faculté d’additionner et de soustraire, les mathématiciens et les autres scientifiques de l’époque ont pu accroître leur efficacité de calcul. Sans l’usage des logarithmes, Kepler n’aurait probablement jamais compris le mouvement des planètes et Newton aurait sûrement omis sa découverte de la loi de la gravité.
En quoi toutefois ces logarithmes sont-ils liés au nombre e qui nous intéresse plus que tout ? Et bien c’est que ce nombre possède une particularité liée au logarithme. Si à l’époque de Napier, la base la plus courante était 10, on savait tout de même que d’autres bases pouvaient être utilisées si nécessaire. La spécificité de e est de servir de base pour définir le logarithme népérien, nommé ainsi en hommage à Napier, plusieurs années après sa mort. Bien que son collègue William Oughtred semble avoir utilisé e en appendice d’un traité de Napier en 1618, Oughtred n’aurait jamais proprement reconnu la constante comme telle.
Il faudra donc attendre l’apport d’autres mathématiciens pour que s’étende la compréhension du nombre e. D'ailleurs, la dénomination « e » arrivera seulement 100 ans plus tard, avec Euler. Toutefois, avant le travail de ce grand mathématicien, d’autres savants ont contribué à améliorer la compréhension du nombre e.
Le nombre e et l’aire sous l’hyperbole
Quelques années plus tard, en 1647, le mathématicien belge Grégoire de Saint-Vincent s’intéresse à la courbe
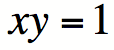 qu’on peut également lire
qu’on peut également lire 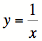 . Dans le modèle fonctionnel actuel, on définit souvent cette équation
comme celle de la fonction rationnelle. Cependant, Saint-Vincent étudie
cette courbe comme celle d’une hyperbole, dont les deux branches
figurent respectivement dans les quadrants I et III du plan cartésien.
Dans son étude, le mathématicien cherche particulièrement à calculer
l’aire sous la courbe de la branche de l’hyperbole du premier quadrant.
Il découvre en effet une équivalence entre les aires de certaines
régions. Par exemple, l’aire sous la courbe entre les valeurs de x égale à 1 et 1,5 est la même que l’aire sous la courbes entre les valeurs 2 et 3, ces deux couples de valeurs étant dans la même proportion.
. Dans le modèle fonctionnel actuel, on définit souvent cette équation
comme celle de la fonction rationnelle. Cependant, Saint-Vincent étudie
cette courbe comme celle d’une hyperbole, dont les deux branches
figurent respectivement dans les quadrants I et III du plan cartésien.
Dans son étude, le mathématicien cherche particulièrement à calculer
l’aire sous la courbe de la branche de l’hyperbole du premier quadrant.
Il découvre en effet une équivalence entre les aires de certaines
régions. Par exemple, l’aire sous la courbe entre les valeurs de x égale à 1 et 1,5 est la même que l’aire sous la courbes entre les valeurs 2 et 3, ces deux couples de valeurs étant dans la même proportion. 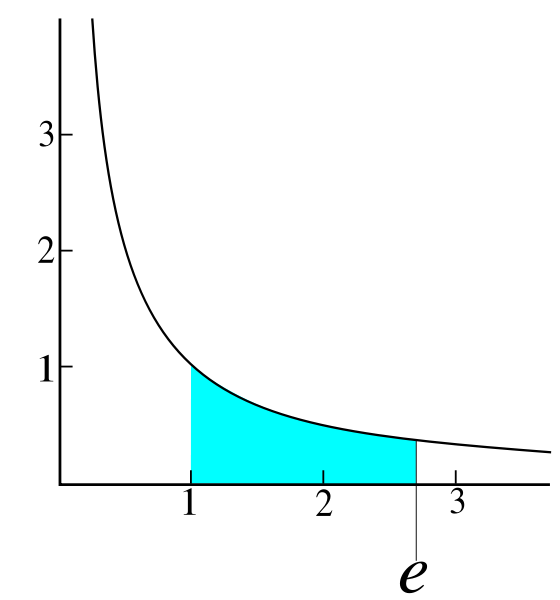
Deux ans plus tard, cette découverte permet à Alphonse Antoine de Sarasa, un élève de Saint-Vincent, d’établir un lien entre les fonctions logarithmiques et l’aire sous la courbe de l’hyperbole. Il en découle que l’aire sous la courbe entre les valeurs de x égale à 1 et à e est exactement 1 (il s’agit de l’aire de la région bleutée sur la figure ci-contre).
Sous un angle algébrique, cela implique que :
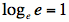
ou comme le symbole usuel du logarithme népérien le veut,
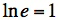 .
. Les intérêts composés
Quelques années plus tard, dans un tout autre domaine des mathématiques, le suisse Jacques Bernouilli (dont le portrait se trouve ci-dessous) trouve une nouvelle approche pour définir le nombre e, et ce, grâce aux intérêts composés. Au XVIIe siècle, les intérêts sur les prêts étaient déjà connus depuis bien longtemps. Bernouilli se demande toutefois comment calculer l’intérêt de manière composée. Ce principe repose sur le fait d’ajouter le plus fréquemment possible les intérêts accumulés au montant initial déposé, afin d’augmenter son gain. Dans son expérience, Bernouilli calcule le montant obtenu si 1 dollar est déposé à 100% d’intérêt.
 Si
l’intérêt du capital est calculé annuellement, on obtient 2 dollars à
la fin de l’année. Si l’intérêt est calculé mensuellement, on obtient
alors 2,61 dollars à la fin de l’année, ce qui est bien. Si l’intérêt
est plutôt calculé quotidiennement, on obtient
2,71 dollars à la fin de l’année, ce qui est beaucoup mieux! Or, si on
calcule l’intérêt chaque seconde, on obtient toujours 2,71 dollars.
Voilà qui semble bien curieux… L’idée de Bernouilli
était que le montant obtenu augmenterait nécessairement si le nombre de
fois qu’on calculait l’intérêt augmentait, mais il semble que non. Par
ce calcul, Bernouilli venait en fait de découvrir la constante e.
Si
l’intérêt du capital est calculé annuellement, on obtient 2 dollars à
la fin de l’année. Si l’intérêt est calculé mensuellement, on obtient
alors 2,61 dollars à la fin de l’année, ce qui est bien. Si l’intérêt
est plutôt calculé quotidiennement, on obtient
2,71 dollars à la fin de l’année, ce qui est beaucoup mieux! Or, si on
calcule l’intérêt chaque seconde, on obtient toujours 2,71 dollars.
Voilà qui semble bien curieux… L’idée de Bernouilli
était que le montant obtenu augmenterait nécessairement si le nombre de
fois qu’on calculait l’intérêt augmentait, mais il semble que non. Par
ce calcul, Bernouilli venait en fait de découvrir la constante e.Le procédé qui vient d’être exposé se nomme le calcul de la limite de l’expression
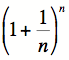 .
. (voir la section Curiosités liées au nombre e pour plus de détails).
D’autres définitions pour e
Dans les années qui suivirent le travail de Bernouilli sur les intérêts composés, Euler entreprit de considérer le nombre e avec rigueur. Tel que mentionné plus tôt, c’est lui qui le nomma officiellement ainsi. Si on ignore la véritable raison du choix de la lettre e pour traiter la singulière constante, plusieurs aiment croire qu’on l’attribue à la première lettre du nom du mathématicien Euler, ou encore à la première lettre du mot « exponentiel ». D’autres suggèrent qu’il s’agit simplement de la première lettre de l’alphabet disponible dans les travaux d’Euler.

Ainsi, au milieu du XVIIIe siècle, le mathématicien de grande renommée Euler (figure ci-contre) s’intéresse au nombre e. Il cherche en fait de nouvelles façons de l’obtenir. Il détermine d’abord le développement de e en série tel que :
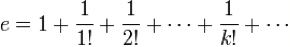
Note : Le calcul d’une valeur en notation factorielle s’obtient en effectuant le produit de tous les entiers naturels allant de 1 jusqu’au nombre cherché.
Par exemple :
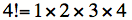
Donc, plus on augmente la valeur de k pour laquelle on effectue le calcul, plus la valeur obtenue se rapproche de e.
Euler élabore également une autre technique d’estimation du nombre e, basée sur le développement des fractions continues.
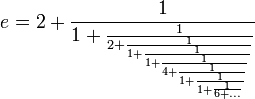
Cette technique permet d’affirmer que le nombre e est bien un nombre irrationnel, soit un nombre dont le développement décimal est infini et ne présente aucune régularité. Par ailleurs, une preuve de l'irrationnalité de e est donnée dans la rubrique du même nom de ce site.
À l’époque, Euler est parvenu à déterminer avec exactitude les 18 premières décimales du nombre e. De nos jours, tout comme pour le nombre irrationnel π, des mathématiciens de tous genres cherchent à calculer de nouvelles décimales au nombre e. Le dernier record est détenu depuis 2007 par Shigeru Kondo et Steve Pagliarulo avec cent mille millions de décimales.
Bibliographie
- BENTLEY, Peter J. Livre des nombres, Sélection du Reader’s Digest (Canada), Montréal, 2008.
- KATZ, Victor. A History of Mathematics, An Introduction, New York, 1992.
- MAOR, Eli. The story of a number, Princeton University Press, Princeton, 1994.
- MONKA, Yvan. Le nombre e, (Page consultée le 21 mars 2010)

